
Презентация "Теорема, обратная теореме Пифагора"

Краткое описание документа:
Презентация «Теорема, обратная теореме Пифагора» предназначена для изучения соответствующей темы курса геометрии 8 класса. При помощи презентации учитель продолжает формировать умение доказывать геометрические утверждения восьмиклассниками. Тема имеет большое практическое значение и используется для решения задач при дальнейшем изучении науки.
Выбранная форма наглядного пособия – мультимедийный материал – оправдана наличием таких инструментов, как анимация, возможность выделения цветом понятий, разделение цветом различных частей учебного материала для улучшения понимания и запоминания.
Презентация содержит формулировку и доказательство теоремы, обратной теореме Пифагора и рассмотрения пифагорова треугольника с выведением общего правила формирования сторон треугольника.

слайды 1-2 (Тема презентации "Теорема, обратная теореме Пифагора", теорема)
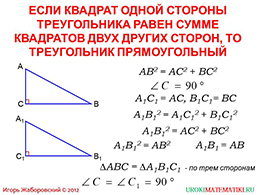
Перед объяснением нового материала необходимо повторить теорему Пифагора. Продолжая формировать навык формулировки обратных утверждений, ученикам предлагается сформулировать теорему, обратную теореме Пифагора, самостоятельно. После формулировки учениками, открывается теорема, выделенная красным цветом для запоминания на экране проектора. На слайде приводится подробное стандартное доказательство теоремы. Демонстрируется рисунок прямоугольного треугольника с обозначением его углов.
По теореме Пифагора приводится алгебраическое выражение закона применительно к данному треугольнику с углом С=90°, что является заключением теоремы Пифагора. Доказываем, что треугольник, для которого верно подобное утверждение, является прямоугольным. Строим другой треугольник, у которого соответствующие стороны попарно равны с первым. Соответственно A1C1 = AC, B1C1= BC. По условию утверждения квадрат стороны A1B1 равен сумме квадратов сторон A1C12 и B1C12.
Вследствие равенства соответствующих сторон первого треугольника, и так как квадрат третьей стороны первого треугольника равен квадрату третьей стороны второго треугольника, то по трем сторонам данные треугольники являются равными. В равных треугольниках и соответствующие углы равны, то есть второй треугольник – прямоугольный. На слайде дано доказательство в схематичном виде. Если требуется словесное описание хода рассуждений, ученики записывают его в тетрадь самостоятельно. Отображенное на слайде в данном виде доказательство запомнить легче.
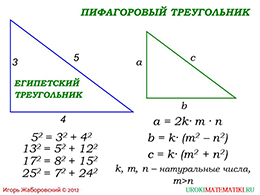
слайд 3 (Египетский треугольник)
На втором слайде производится описание египетского треугольника. Учителем дается описание египетского треугольника как прямоугольного треугольника с соотношением сторон 3:4:5. Далее в качестве примеров прямоугольных треугольников приводятся пифагоровы треугольники, в которых их стороны целочисленные. Продемонстрировав данные треугольники, выводятся общие правила, как образуются значения сторон таких прямоугольных треугольников.
В каждом выражении есть четное число. Его обозначают в виде выражения 2k•m•n. Соответствующие другие стороны прямоугольного треугольника образуются следующим образом: оставшийся катет будет равен k•(m2–n2), а гипотенуза определяется как k•(m2+n2). Данное утверждение верно для натуральных k, m, n, при этом m должно быть больше n. По числам, удовлетворяющим данным условиям, всегда можно построить прямоугольный треугольник. Подобные тройки чисел называют пифагоровыми тройками.
Презентация «Теорема, обратная теореме Пифагора» может быть использована учителем для сопровождения объяснения нового материала по данной теме в качестве наглядного материала. Также подробная схема доказательства теоремы может быть полезна при дистанционном обучении и рекомендована для самостоятельного изучения.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9357 |
| Номер материала | 335 |