
Урок "Площадь трапеции"

Краткое описание документа:
На предыдущих уроках геометрии учащиеся 8-го класса познакомились с понятием площади многоугольника и научились находить площадь квадрата, прямоугольника, параллелограмма и треугольника. С помощью данного видеоурока продолжим изучение площадей геометрических фигур и рассмотрим, как находится площадь трапеции.
Для начала вспомним второе свойство о площади многоугольников. Когда многоугольник разделен на несколько многоугольников, то площадь исходного многоугольника можно вычислить как сумму площадей многоугольников, его составляющих. Это свойство мы применим для нахождения площади трапеции. Также необходимо вспомнить, как вычисляется площадь треугольника. Значение площади треугольника находится как произведение его высоты на основание, деленное на 2. Если у школьников возникли вопросы по прошлым темам, можно вернуться на несколько шагов назад и повторить изученный материал. Теперь перейдем к нашему видеоуроку.
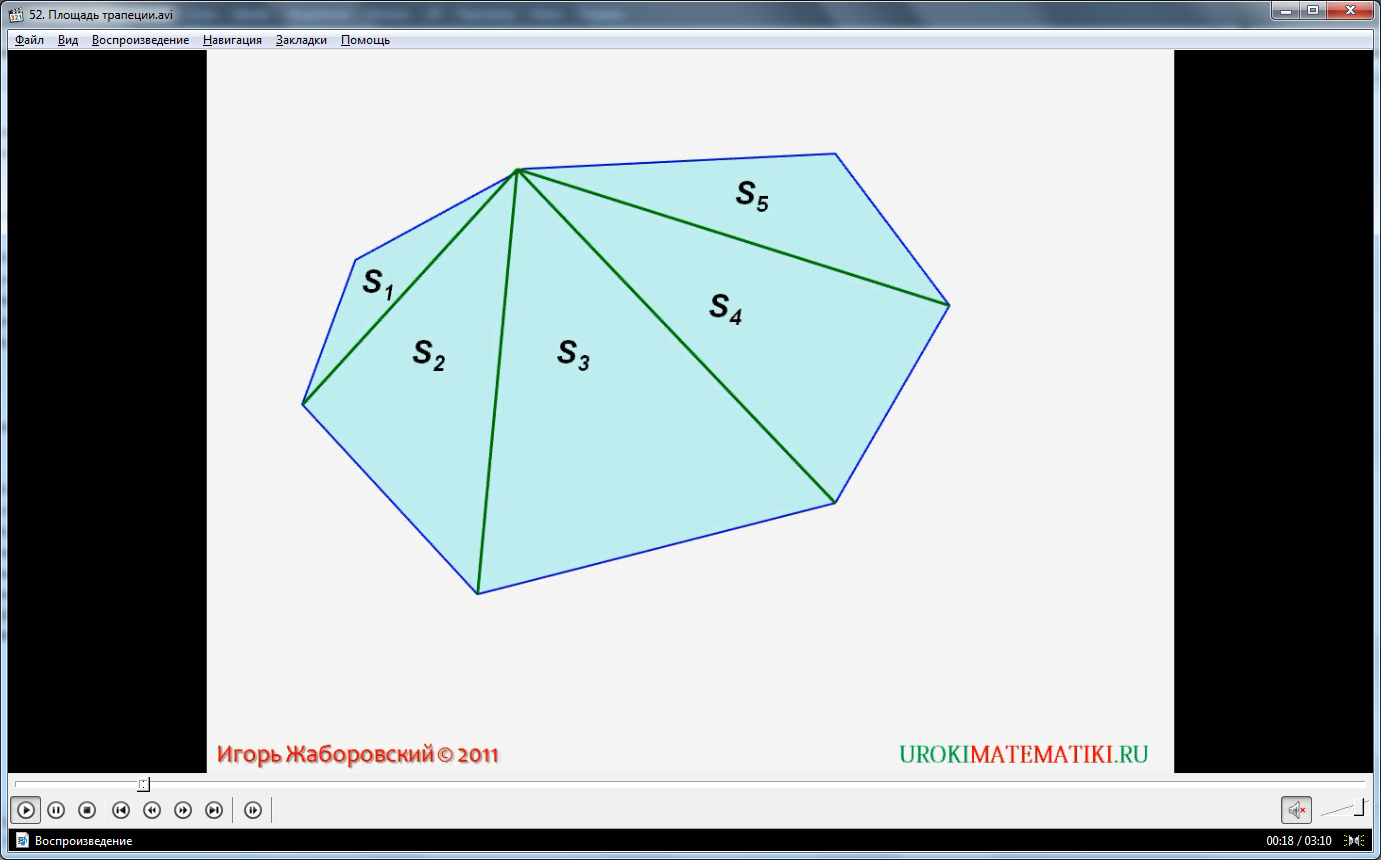
Урок начинается с того, что автор задает вопрос – как можно найти площадь произвольного многоугольника? Автор предлагает следующий способ. Можно разбить многоугольник на треугольники и найти площадь каждого из треугольников. На рисунке мы видим многоугольник, площадь S которого равна сумме площадей треугольников, из которых он состоит: S1 + S2 + S3 + S4 + S5. Используя этот метод, мы можем вывести формулу нахождения площади трапеции.
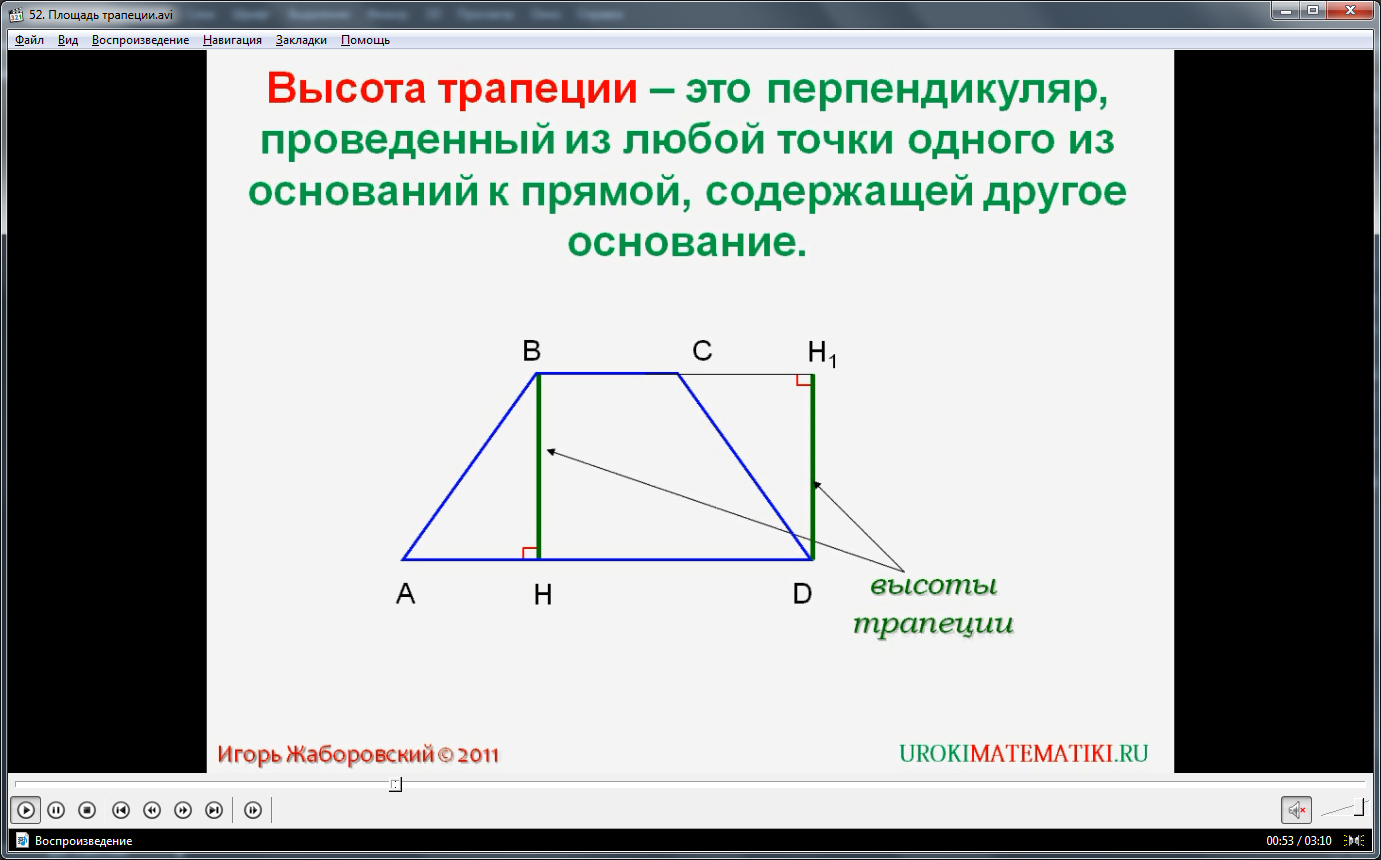
Для более удобного рассмотрения темы введем следующие положения. Высотой трапеции будем называть отрезок, перпендикулярный прямой, которая содержит основание, проведенный из точки другого основания. В трапеции ABCD, которая показана на рисунке, обозначены высоты BH и DH1.
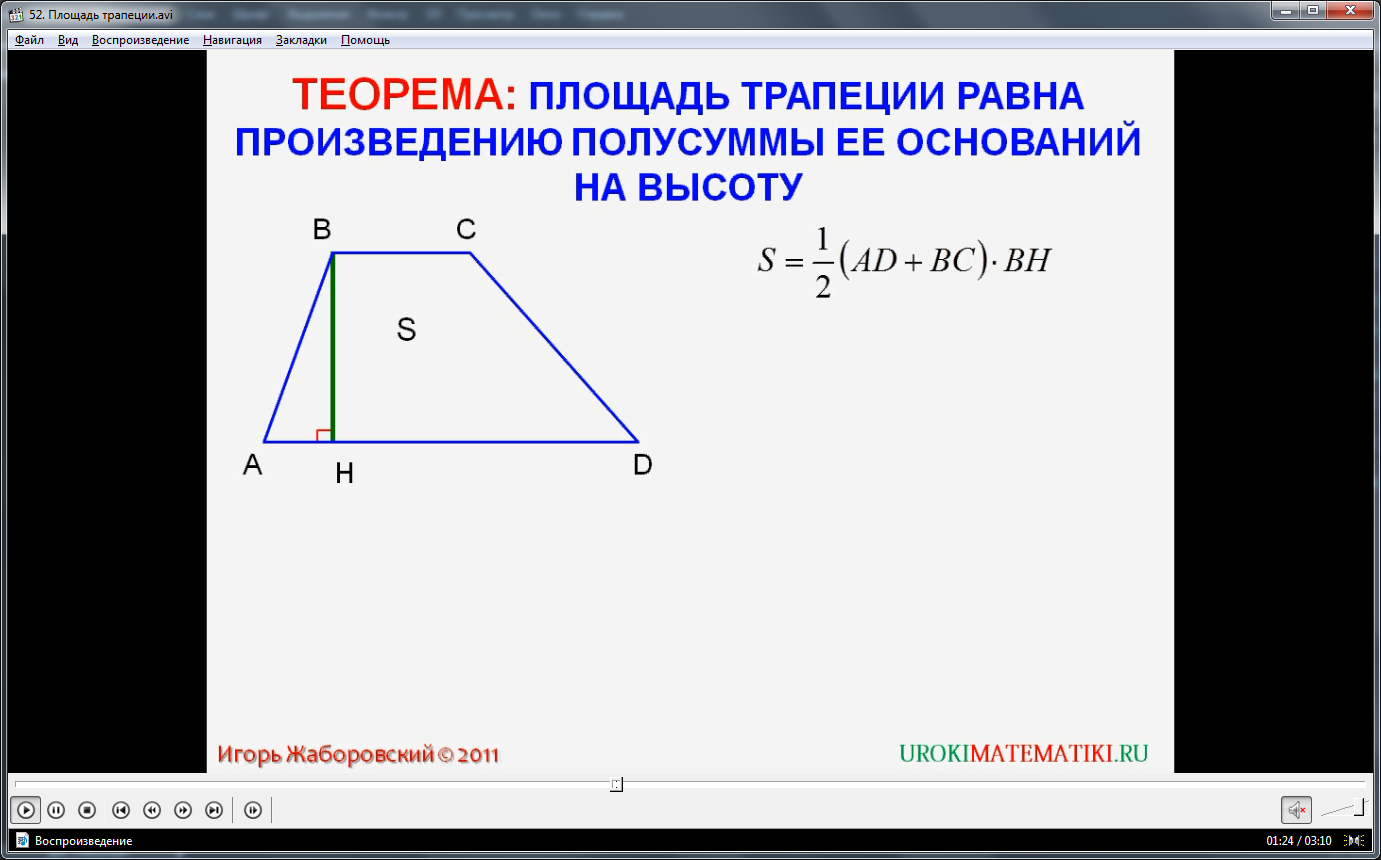
Рассмотрим теорему. Площадь трапеции находится как произведение высоты на значение суммы ее оснований, которое разделено пополам. Необходимо доказать данное утверждение.
Допустим, дан многоугольник ABCD – трапеция, где стороны AB и DC являются основаниями, отрезок BH – высотой. Площадь трапеции выражается как значение S. Докажем, что S = 0,5 (AD + BC) x BH.
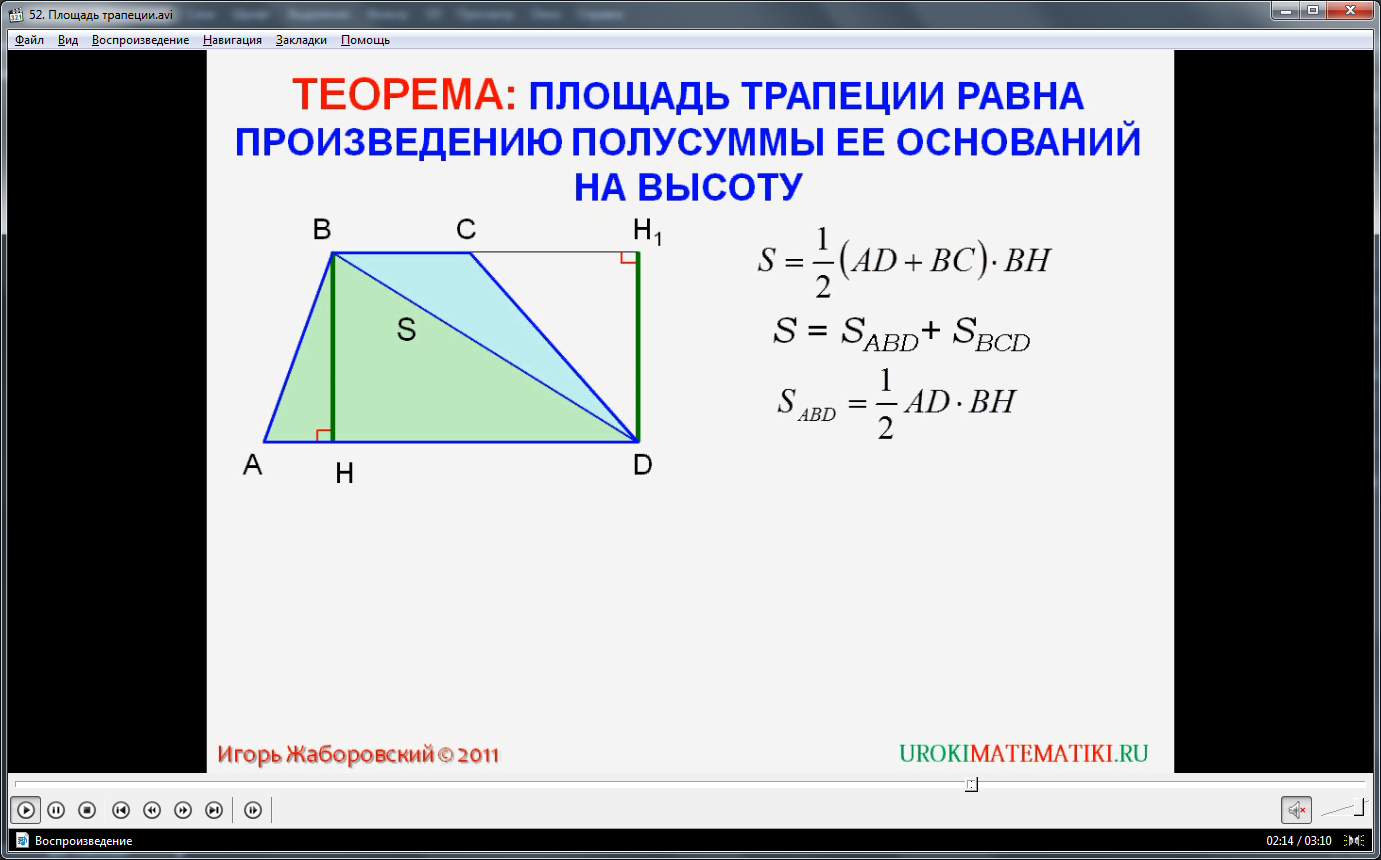
Проведем диагональ DB, она разделит трапецию на треугольники ADB и CDB. Тогда площадь трапеции будет равна сумме площадеймногоугольников, из которых она состоит. А именно – сумме площадей треугольников: S = SABD + SBCD.
Рассмотрим треугольники ADBи CDB. Сторону DA будем считать основанием, а перпендикуляр BH – высотой треугольника ADB. Отрезок BC примем за основание, а отрезок DH1 за высоту треугольника CDB.
Применяя теорему о площади треугольника запишем, чему будут равны площади треугольников ADИ и CИD. SABD = 0,5 x AD x BH. SBCD = 0,5 x BC x DH1. Отрезки BH и DH1 равны, как высоты трапеции.Тогда площадь треугольника BCD можем записать, заменив DH1 на BH: SBCD = 0,5 x BC xBH. Таким образом, получим S = 0,5 x AD x BH + 0,5 x BC xBH = 0,5 (AD + BC) x BH. Т.е. площадь трапеции равна произведению высоты на деленную на 2 сумму ее оснований. Мы доказали теорему.
Материалы видеоурока будут полезны учителю, как при подготовке, так и при проведении урока.
Информация с легкостью усвоится учениками, так как изложена последовательно, доступно и наглядно.
Все теоретические аспекты, которые изучают ученики в текущих темах по геометрии, будут часто применяться при решении задач в дальнейшем. Поэтому важно не упустить деталей и хорошо запомнить новый материал. Представленный видеоурок станет основой удобного и легкого обучения.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4758 |
| Номер материала | 590 |