
Презентация "Теорема синусов"

Краткое описание документа:
Тригонометрия – это целый раздел, которому нужно уделить огромное количество часов, чтобы понять полноценно. С основными тригонометрическими понятиями и тождествами школьники могут познакомиться, пользуясь предыдущими презентациями. Желательно, что данная тема была хорошо объяснена учителем, и были прокомментированы каждые моменты. Школьники, которые собираются просмотреть материал данного документа, должны знать и понимать, что такое синус, косинус и тангенс. Также, они должны уметь находить синусы некоторых углов прямоугольных треугольников. Основное тригонометрическое тождество также стоит вспомнить.


Перейдем к рассмотрению, непосредственно, данной презентации. На первом слайде выводится теорема, которая будет ниже рассмотрена. Суть теоремы в пропорциональности сторон и синусов противолежащих углов. Сразу же можно заметить, что изображен треугольник ABC. Для удобства, напротив каждого угла обозначены соответствующие прописные буквы, например, напротив угла A сторону CBусловно обозначили через a. Это приводит к более удобным записям. Школьники в данном возрасте должны уже привыкнуть к подобным заменам, ведь им придется работать с большими выражениями.
После замены можно увидеть, непосредственно, теорему, записанную в алгебраическом виде, то есть, формулу. Формула обведена в рамку, для того, чтобы педалировать на ней внимание пользователя.
Зная формулу нахождения площадей треугольников, можно выразить три варианта ее записи через стороны и синусы углов между ними. Так как площадь в результате должна иметь одно и то же значение во всех случаях, то правые части всех этих выражений равны. После набольших преобразований, можно убедиться, что теорема является истинной и доказана.
Далее рассматривается иная ситуация. Здесь приводится несколько другие рассуждения. Используются знания, связанные со свойствами описанных и вписанных окружностей. На данном примере, треугольник описан окружностью с радиусом R. Отношение сторон на синус противоположных углов равняется диаметру окружности, то есть 2R, в которую вписан рассматриваемый треугольник.
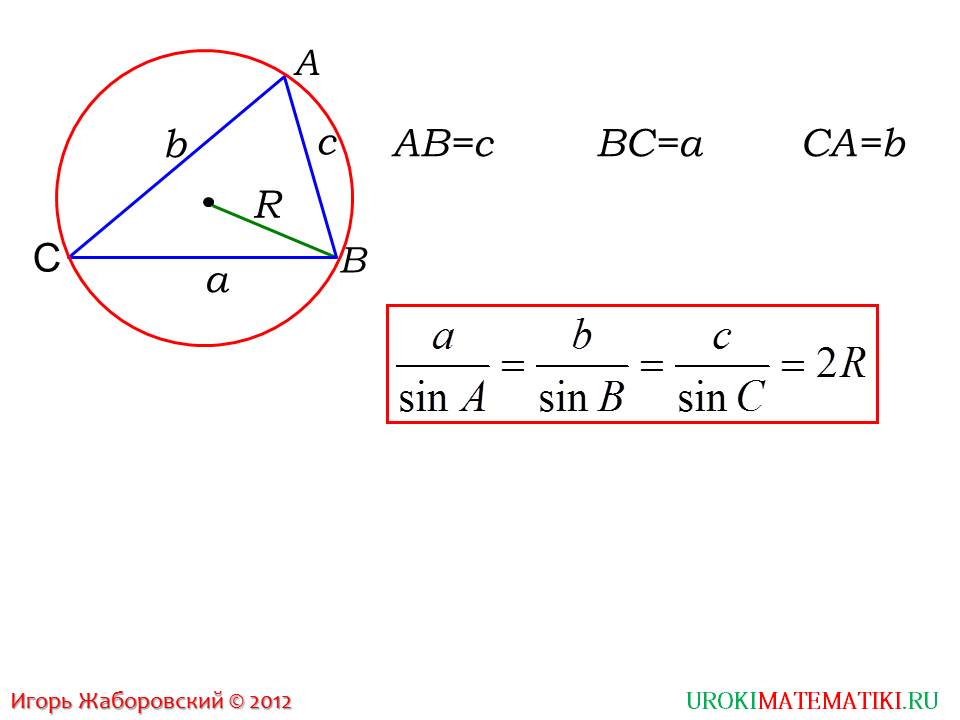
Данные соотношения могут, во многом, помочь при решении различных геометрических задач. Они пригодятся при нахождении сторон различных треугольников, которые можно выразить из пропорций. Школьник, изучивший материал данной презентации, может попробовать применить формулы на практике.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6310 |
| Номер материала | 703 |