
Презентация "Тригонометрические функции числового аргумента"

Краткое описание документа:
Данная презентация является последовательным и понятным обучающим материалом, который относится к разделу «Тригонометрия». Состоит она из небольшого количества слайдов, с помощью которых можно изучить такую тему, как: «Тригонометрические функции числового аргумента».

Материал будет полезен не только ученикам, но и начинающим учителям по математике и репетиторам при составлении плана урока либо примеров, которые можно предоставить ученикам. Презентация является достаточно информативной и при правильном сопровождении комментариями и объяснениями сделает процесс обучения более эффективным. Она содержит множество иллюстраций, которые можно продемонстрировать во время урока в школе.
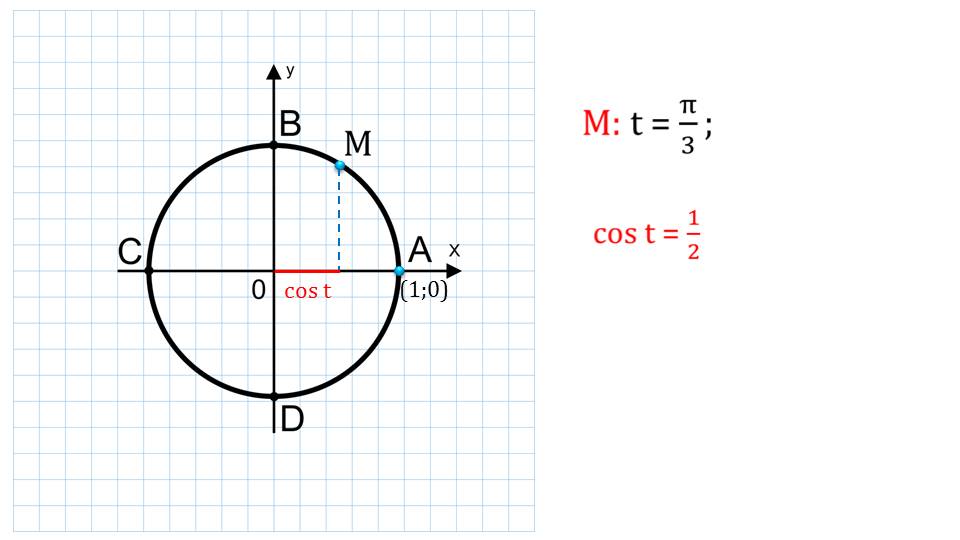
На первом слайде изображена единичная числовая окружность. На ней изображены точки пересечения окружности с осями ОХ и ОУ – A, B, C, D.


На окружности выбрана произвольным образом точка М, для которой найден косинус. Как он был найден? Для этого проведен перпендикуляр от точки к оси ОХ. Расстояние от начала координат и до точки пересечения перпендикуляра с ОХ показывает значение аргумента. Метод нахождения косинуса является геометрическим. Это наглядно видно на графике.
На следующем слайде приведены значения аргументов для некоторых часто используемых чисел. Далее приводится напоминание основного свойства тригонометрии. Оно гласит о том, что сумма квадратов косинуса некоторого числа и синуса этого же числа равняется единице.

Также напоминаются формулы нахождения тангенса и котангенса. Последнее правило гласит о том, что произведение тангенса некоторого числа и котангенса этого же числа равняется единице. Это можно легко проверить.
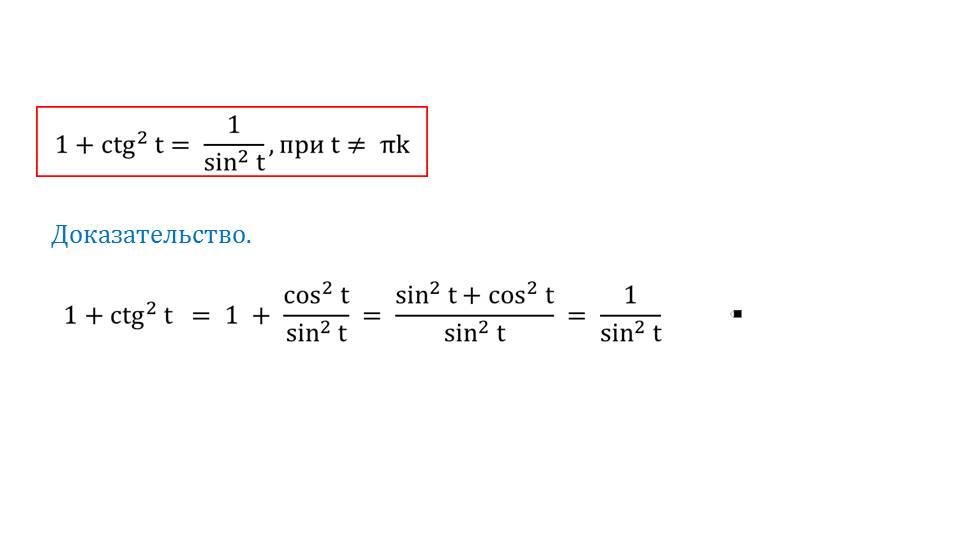
На следующем слайде приводится еще одно утверждение, которое поможет при упрощении огромных сложных на первый взгляд тригонометрических выражений. Доказательство данного утверждения является небольшим и достаточно понятным для десятиклассника. Приводит еще одна теорема, которая касается котангенса.
Эти свойства и теоремы пригодятся при решении последующих примеров, которые демонстрируются в презентации. Параллельно с решениями на экран выводятся формулы, которые были использованы в том или ином случае.
Данная презентация поможет разобраться с одной из важных тем из области тригонометрии. Полученные знания пригодятся при дальнейшем изучении.

При решении различных примеров можно обратиться к данному учебному материалу за помощью. Задачи, продемонстрированные в данном слайде, помогут справиться с другими подобными примерами. Чем больше школьник прорешает практических примеров, тем лучше ему запомнятся формулы и теоремы, изученные на протяжении урока. В противном случае материал может очень быстро забыться.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4336 |
| Номер материала | 788 |