
Презентация "Тригонометрические функции углового аргумента"

Краткое описание документа:
Данная тема является одной из множеств тем, которые охватываются областью «Тригонометрия», которая будет изучаться в 10 классе. Она тесно связана и с алгеброй и с геометрией. Для того чтобы понять суть данной презентации, необходимо предварительно вспомнить свойства треугольников, делая упор на свойства и особенности прямоугольного треугольника. Необходимо вспомнить свойства катетов и гипотенузы, повторить теорему Пифагора.

Начинается презентация с утверждения, указывающего на то, как необходимо находить синус, косинус, тангенс и котангенс некоторых острых углов в прямоугольном треугольнике. Для того чтобы найти синус некоторого острого угла в прямоугольном треугольнике, необходимо посчитать отношения противолежащего катета к гипотенузе. Для того чтобы найти косинус – необходимо составить отношение прилежащего катета к гипотенузе. Что касается тангенса и котангенса острого угла, то необходимо составить отношения катетов. В случае тангенса числителем будет являться противолежащий катет, а котангенса – прилежащий.


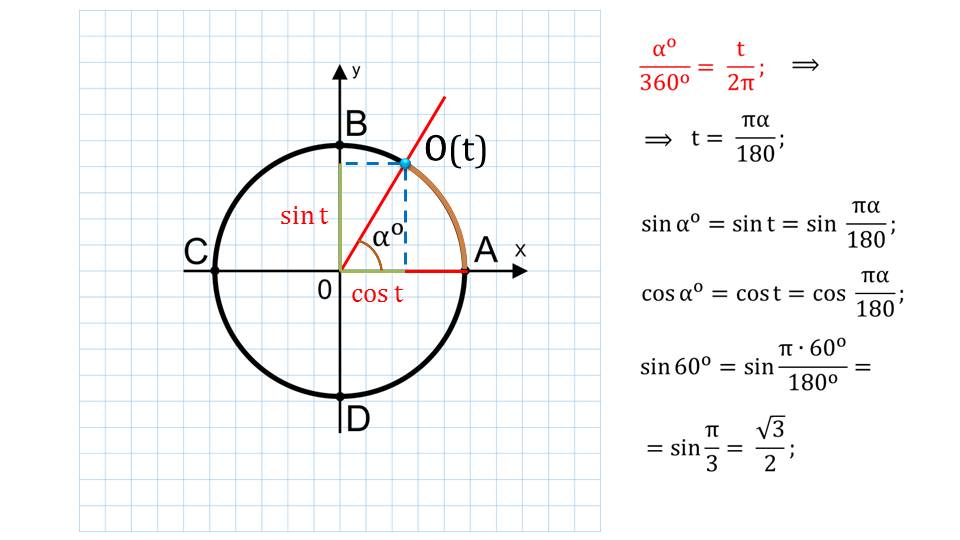
Данное утверждение выводится на первый слайд. Его можно переписать в тетради. Чтобы стало более понятно. На втором слайде выводится иллюстрация единичной окружности. На ней обозначены оси – х и у, обозначены точки пересечения окружности с осью абсциссы и ординаты, показано начало координат. Мы видим, что на окружности выбрана произвольным образом точка О. Геометрически найдены косинус и синус. Для этого проведены перпендикуляры от данной точки. Перпендикуляр к оси ОХ указывает на значение косинуса, а к оси ОУ – на значение синуса. Легко заметить, что на иллюстрации образовался прямоугольный треугольник с острым углом альфа. Также видно, каким образом находится синус данного угла, с использованием знания о прямоугольном треугольнике.
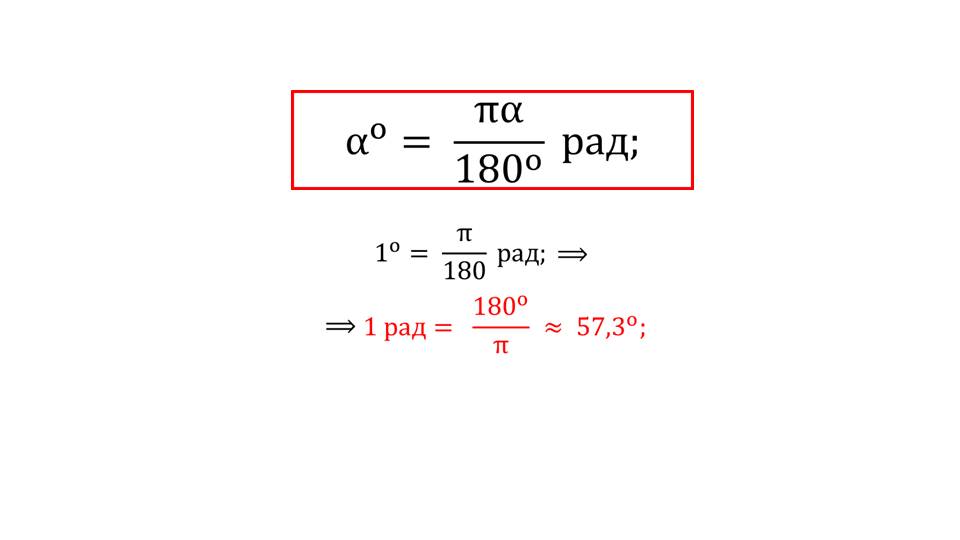
Следующая часть презентации посвящена обозначениям угла. Угол может быть обозначен как через градусную меру, так и радианную. Радиан обозначается сокращенно – «рад». С обозначением градуса школьники ознакомлены ранее. Один градус составляется 1/360 длину окружности. Это можно увидеть на иллюстрации. Учитель может прокомментировать данный момент более подробно, чтобы у школьников не возникло непонимание. Что же такое радиан? Это также центральный угол, то есть вершина находится в начале координат и имеет опор на дугу. 1 радиан приблизительно равен 57,3 градуса. Откуда появилась эта константа, можно понять очень просто. Объяснения приведены в презентации.

После того, как изучены основные понятия и рассмотрены все моменты, приводятся практические примеры. Они демонстрированы вместе с решением пошагово очень подробно.


Таким образом, 10-классники могут понять, каким образом действует соответствие между градусной мерой и радианной. Это очень важно понимать при изучении тригонометрии, ведь в ней по большей части делается упор на использование именно радианной меры.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5079 |
| Номер материала | 790 |