
Презентация "Уравнения с параметрами"

Краткое описание документа:
Презентация «Уравнения с параметрами» - наглядный материал для ведения урока математики по данной теме. Тема имеет важное практическое значение. Ее элементы рассматривались ранее, поэтому задача данного урока – систематизировать полученные знания, рассмотреть уравнения с параметрами как отдельный объект. В ходе презентации вводятся понятия, которыми необходимо оперировать в ходе решения уравнений с параметрами, описываются решения различных уравнений с параметрами. Презентация – один из лучших способов обеспечения наглядности.
Подготовленный материал помогает последовательно подать учебную информацию. Использование анимационных эффектов, выделение важных понятий цветом способствует удержанию внимания учеников на изучаемом предмете, более быстрому запоминанию теоретического материала, лучшему усвоению методов решения математических задач.


Презентация начинается с напоминания, какие обозначения традиционно используют в записи математических выражений. На первом слайде отмечается, что неизвестные величины обычно обозначают буквами х, у, z… - последними в латинском алфавите. Числовые значения, называемые параметрами, обозначают первыми буквами латинского алфавита – а, b, c... Вводится понятие уравнения с параметрами – уравнения вида f(x;a)=0, вкотором нужно найти х, а буквой а обозначено любое действительное число. Определение уравнения с параметрами выделено для запоминания в рамку, важные понятие окрашены в красный цвет. Также указывается, что означает решить уравнение с параметром. На слайде 3 формулируется определение, что решить уравнение с параметром означает найти множество его корней для каждого значения параметра или доказать их отсутствие. После рассмотрения теоретических основ решения уравнений с параметрами описывается решение различных задач, требующих данных навыков.


На слайде 4 описывается решение уравнения ах=1. Очевидно, в данном уравнении х - переменная, а – параметр. Чтобы найти решение уравнения, необходимо оценить весть спектр значений, которые может принимать х. Сначала рассматривается случай, когда а≠0. В этом случае переменная х выражается через параметр х=1/а. В случае равенства нулю параметра а уравнение не имеет решений. Таким образом охвачен вся область возможных значений х для каждого действительного а.


В примере 2 требуется решить уравнение а2х-1=х+а. Уравнение преобразуем таким образом, чтобы х можно было выразить через параметр а. Путем переноса членов уравнения из одной части в другую, группировки и выноса общего множителя за скобки, получаем уравнение х(а2-1)= а+1. Переменную х можно выразить через а выражением х=(а+1)/(а2-1) (иначе х=1/(а-1)) в случае соблюдения неравенства а2-1≠0, так как в знаменателе не может быть нуль. Отдельно рассматривается случай, когда а=1. В этом случае получаем уравнение 0·х=2. Из него видно, что при а=1 уравнение не имеет решений. Для а=-1 получаем равенство 0·х=0. Такое равенство будет справедливым при любом действительном х. Соответственно, решение данного уравнения состоит из трех частей – для а≠+-1, для а=1 и для а=-1.
Пример 2 описывает решение уравнения (х-2а)/(х-4)=0. Сначала оценивается область допустимых значений. Отмечается, что в данном уравнении не допускается х-4=0, то есть х≠4. Значит, для получения в результате вычисления нуля возможно только х-2а=0. Отсюда х=2а. Из найденного ограничения находим недопустимое значение а≠2. Соответственно, решение данного уравнение состоит из двух частей – при а≠2 х=2а, а при а=2 уравнение не имеет решений.


В примере 4 решается уравнение |x-a|=2. Для решения данного уравнения с модулем воспользуемся методом, использующим определение модуля. Уравнение преобразуется в систему уравнений х-а=2 и х-а=-2. Из уравнений находим выражение для нахождения переменной х1=а+2 и х2=а-2.
Пример 5 также содержит выражение с модулями |x|+|x-a|=0. Так как оба слагаемых положительные, в сумме они дадут нуль только при равенстве нулю обоих выражений, поэтому уравнение преобразуется в систему уравнений х=0 и х-а=0. Рассматриваем два возможных варианта. В первом случае а=0, тогда и х=0. Во втором случае а≠0, тогда система не имеет решений.
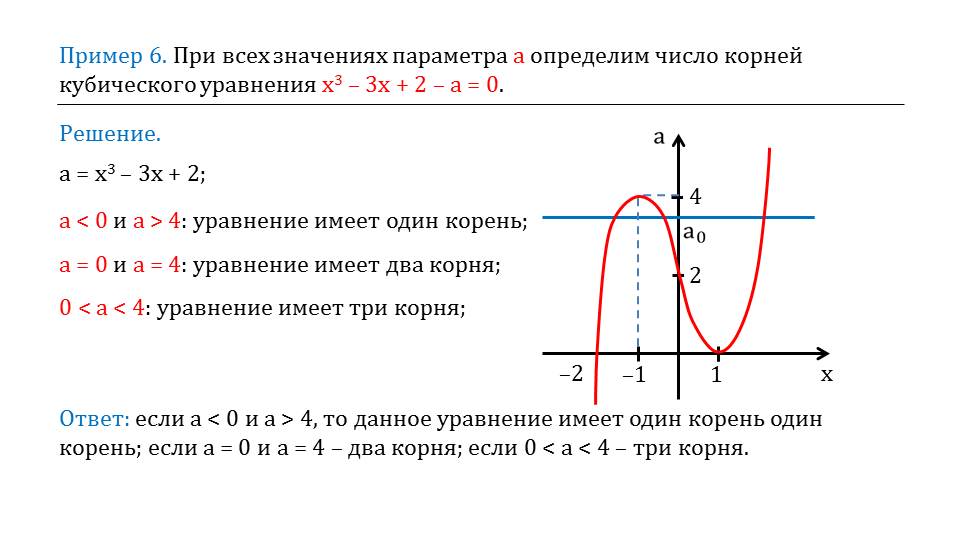
В примере 6 необходимо определить число корней кубического уравнения х3-3х+2-а=0. В решении данного уравнения воспользуемся графическим способом. На координатной плоскости изображается график функции а= х3-3х+2. Анализируя поведение графика функции, находим при а<0 и a>4 исходное уравнение имеет один корень. При значениях а=0 и а=4 в уравнении два корня. На промежутке значений 0<a<4 уравнение имеет три корня. Задача решена.

В примере 7 необходимо решить уравнение mx2+3mx-(m+2)=0. При решении уравнения рассматривается два случая – когда m=0 и m≠0. При подстановке m=0 в уравнение получаем неверное равенство, поэтому в этом случае уравнение не имеет корней. Во втором случае рассматриваем решение квадратного уравнения. Находим дискриминант D=m(13m+8). Чтобы уравнение имело решение, дискриминант должен быть равен нулю или больше нуля. Соответственно, mϵ(-∞;-8/13)U(0;+∞). Решениями уравнения будут х1,2=(1/2m)(-3m+-√(m(13m+8))).
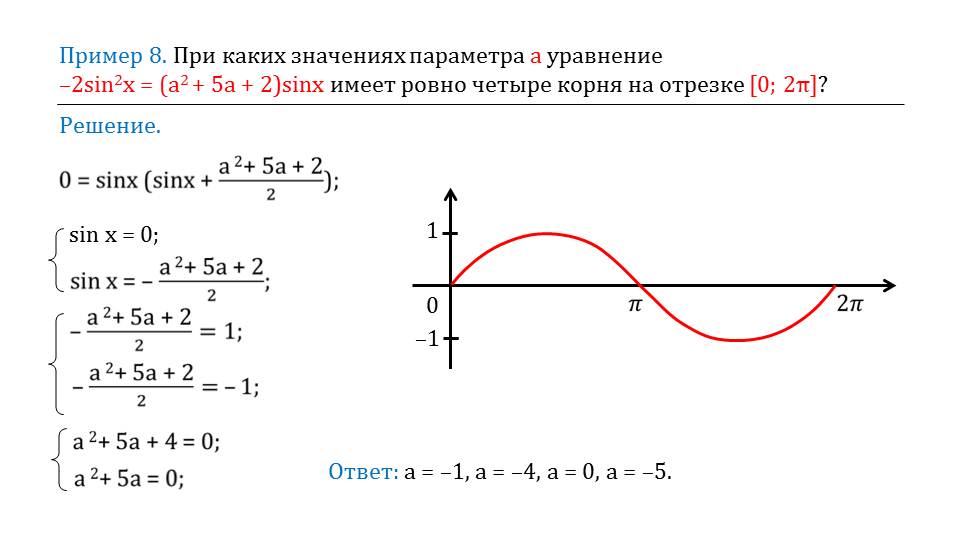
В последнем примере рассматривается решение уравнения с параметром -2sin2x=(a2+5a+2)sinx. В задании требуется определить, при каких значениях параметра данное уравнение имеет 4 корня на отрезке [0;2π]. Чтобы решить данное уравнение, оно сначала преобразуется. После преобразования уравнение представляется произведением 0=sinx(sinx+(a2+5a+2)/2). Данное уравнение будет справедливым, если один из его множителей будет равен нулю, то есть оно превращается в систему уравнений sinx=0 и sinx=-(a2+5a+2)/2. Данная система будет верна при параметре, удовлетворяющем условию системы -(a2+5a+2)/2=1 и -(a2+5a+2)/2=-1, а также a2+5a+4=0 и a2+5a=0. Решениями систем уравнений являются параметры а=-1, а=-4, а=0, а=-5.
Презентация «Уравнения с параметрами» рекомендуется для применения на традиционном уроке математики для повышения его эффективности. Также данное наглядное пособие может помочь учителю, осуществляющему дистанционное обучение, быстрее добиться эффекта от процесса обучения. Подробное описание методики решения уравнений с параметрами на примерах дает возможность приобрести умения использовать теоретические сведения и самостоятельно учеником при работе дома.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6584 |
| Номер материала | 1048 |