
Презентация "Вычисление тангенса и котангенса"

Краткое описание документа:
В 10 классе в курсе изучения алгебры, ученики столкнуться с таким интересным и информативным разделом, как тригонометрия. Она охватывает множество простых и сложных тем, с которыми необходимо справиться. Для того, чтобы понимать уроки как можно лучше, необходимо потратить много времени помимо школы на изучение того или другого понятия, того или иного метода самостоятельно.
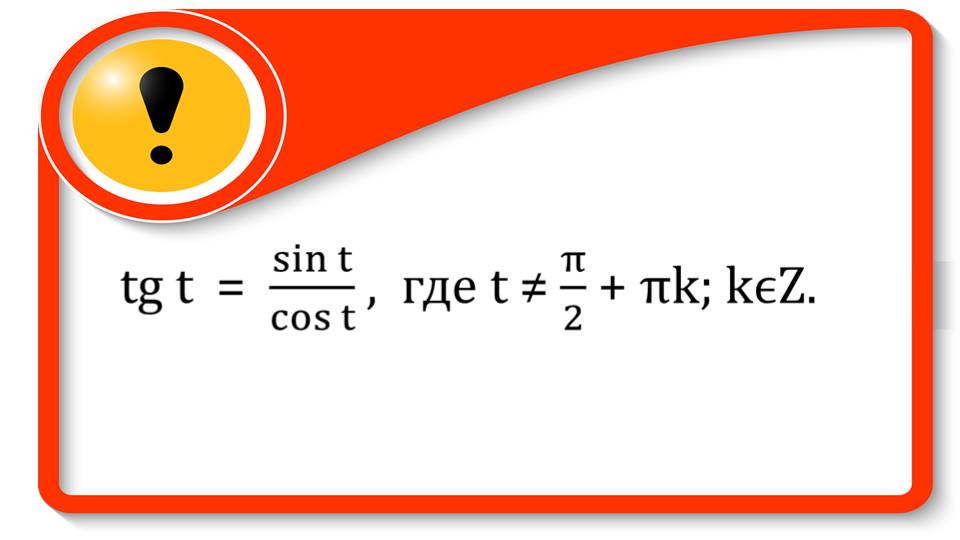

Тригонометрия подразумевает упрощение огромных выражений, для которых необходимо знать большое количество формул и тригонометрических формул. Для того чтобы их запомнить, не нужно жалеть время на решение практических заданий.


После того, как школьники ознакомились с такими понятиями, как синус и косинус, они могут перейти к изучению тангенса и котангенса, ведь это взаимосвязанные понятия. Данная презентация показывает, как можно находить тангенс и котангенс, как они обозначаются, как с ними работать и какими свойствами они обладают. Будут рассмотрены характеристики и примеры.
Тангенс представляет собой дробь, числителем которого является синус искомого числа, а знаменателем – косинус.
Котангенс же представляет собой частное косинуса на синус. Тангенс и котангенс имеют одинаковые знаки на различных четвертях. На первой и третьей четверти они положительны, на второй и четвертой – они отрицательны. Это можно легко проверить на числовых примерах – подставить конкретные значения вместо косинуса и синуса.
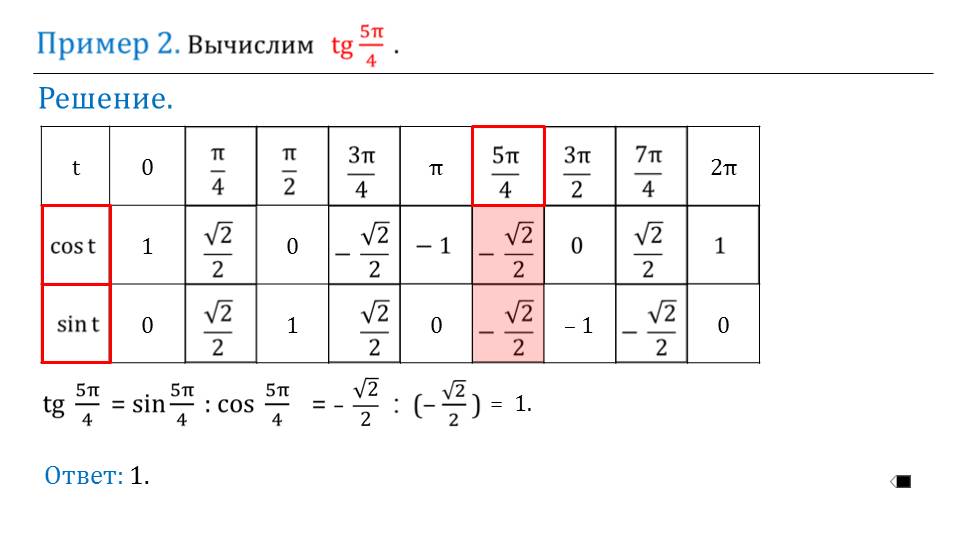
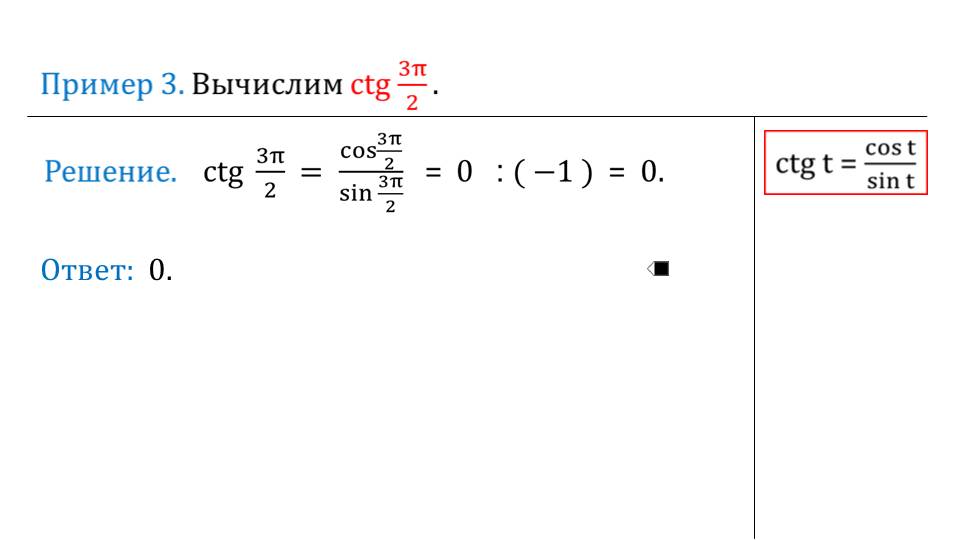
Далее рассматриваются примеры.
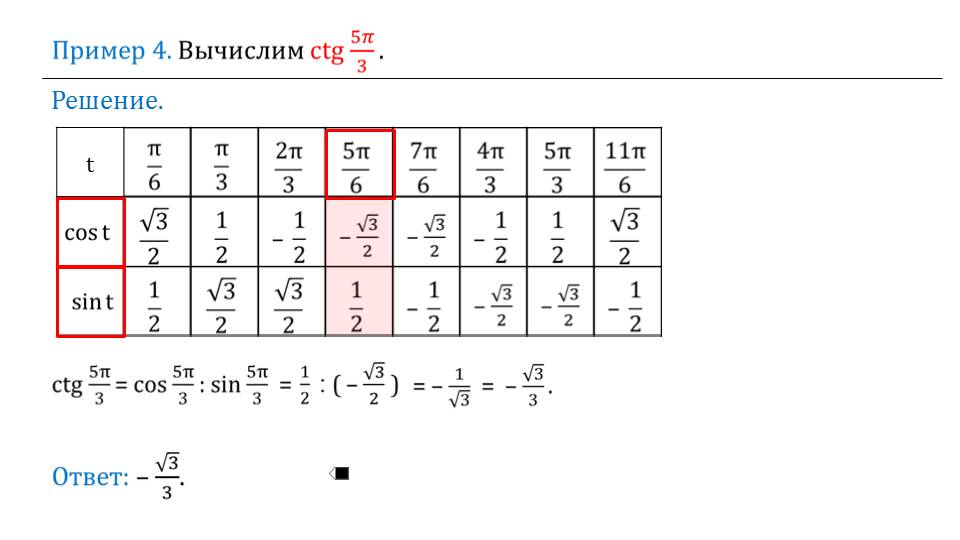

При их решении предлагается вспомнить формулы нахождения тангенса и котангенса, которые ранее были приведены. На втором примере напоминается, как правильно пользоваться таблицей значений. Для лучшего закрепления необходимо дать ученикам примеры для самостоятельного решения.
Чтобы в каждый раз не считать в отдельности тангенс и котангенс, можно создать таблицу, как в случае синуса и косинуса, в котором будут демонстрироваться наиболее частые случаи. В дальнейшем школьники будут довольно часто обращаться к подобным таблицам. Основные значения некоторые учителя требуют запомнить.


Далее приводится теорема, гласящая о том, что тангенс от отрицательного числа равен минус тангенсу этого числа по модулю. Это касается и котангенсу. Приводится пошаговое понятное доказательство, которое смогут понять школьники. Доказательства лучше просматривать вместе с учителем, если уровень ученика недостаточно высокий, либо с репетитором индивидуально.


В отдельности рассматривается синус от отрицательного числа, в отдельности – косинус. Подставляя эти значение в формулы тангенса и котангенса получаем подтверждение данного свойства.
Следующий слайд показывает еще одно свойство вместе с доказательством. Далее указывается на периодичность. Тангенс некоторого числа с добавлением к нему выражения – Пи, умноженное на некоторое целое k, будет равняться тангенсу изначального числа. То же самое касается и котангенсу. Таким образом, они имеют период: пи, умноженное на k. Далее рассматриваются примеры, с помощью которых можно понять лучше данные свойства.

Презентация подойдет для сопровождения урока. С помощью него он станет боле интересным и информативным.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8284 |
| Номер материала | 787 |