
Урок "Решение уравнений с помощью разложения на множители"

Краткое описание документа:
Используя законы преобразования многочленов путем вынесения общего множителя, что мы изучили на прошлых видеозанятиях, можно успешно решать уравнения различного уровня сложности. Приведем некоторые примеры.
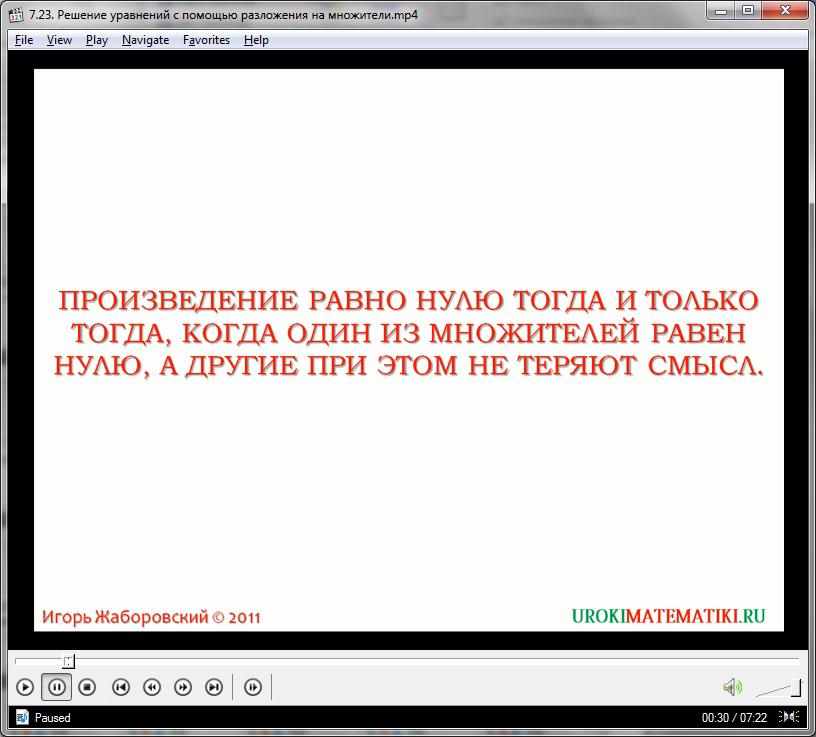
Следует напомнить, что проводить разложение многочлена можно двумя способами. Необходимо либо находить один общий множитель и выносить его за скобки (в которых остается все выражение), либо группировать одночлены по схожим основам и уже с групп выносить множители. Кроме того, стоит усвоить правило базовой математики: произведение некоторых множителей равно нулю тогда и только тогда, когда один из множителей равен нулю, а остальные являются натуральными числами.
Рассмотрим первый пример. Дано уравнение, нужно найти его корень:
5х2 – 15х = 0
Преобразуем левую часть равенства, использовав вынесение общего множителя 5х за скобки. Получим систему уравнений, использовав правило для нулевого произведения:
5х2 – 15х = 0
5х(х – 3) = 0
5х = 0
х – 3 = 0
Как видим, корнями уравнения являются два значения – 0 и -3.
Второй пример. Необходимо решить уравнение:
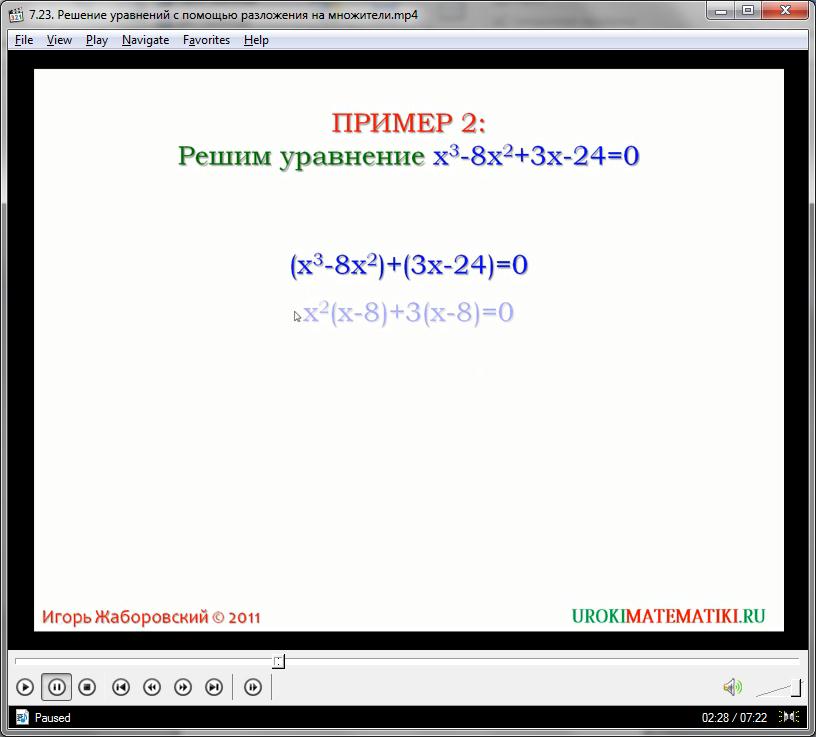
х3 – 8х2 + 3х – 24 = 0
Используя способ группировки, получаем две группы одночленов, при этом в первой из них общее основание равно х2, а во второй – трем. Выносим множители за скобки:
х3 – 8х2 + 3х – 24 = 0
(х3 – 8х2) + (3х – 24) = 0
х2(х – 8) + 3(х – 8) = 0
У нас появились идентичные выражения в обеих скобках. Это позволяет представить многочлен в левой части уравнения как произведение полиномов – используя вынесение (х – 8) за скобки:
х2(х – 8) + 3(х – 8) = 0
(х – 8)(х2 +3) = 0
Памятуя о том, что произведение любых выражений, равных нулю, возможно только тогда, когда одно из выражений равно нулю, можем записать систему уравнений, тождественных между собой, и исходящих от начального примера. Решаем эти уравнения:
х – 8 = 0
х = 8
х2 + 3 = 0
х2 = -3
Второй корень недействителен, так как квадрат его равен отрицательному числу, что противоречит закону о квадратной степени (обнуляющей минус). Поэтому корректным ответом является только первое значение переменной х, равное восьми.
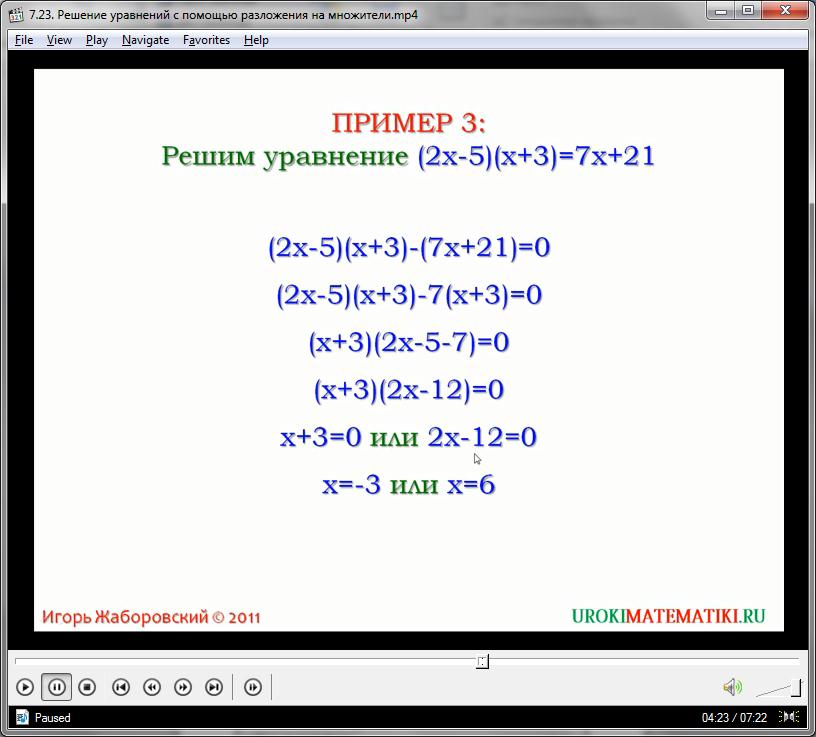
Более сложные уравнения построены так, что ни одна из частей выражения не приравнена напрямую к нулю. В этом случае следует понимать, что любое равенство можно преобразовать так, чтобы в правой части остался ноль. Законы алгебры позволяют с легкостью переносить любые элементы с одной части уравнения в другую и наоборот. Важно учитывать инверсию знаков при этой операции. Рассмотрим пример. Необходимо решить уравнение вида:
(2х – 5)(х + 3) = 7х + 21
Чтобы решить эту задачу, необходимо переместить все одночлены в левую часть, приравнивая полученный многочлен к нулю, а потом преобразовать выражение слева, образуя произведение любых подходящих множителей.
Для этого производим перемещение (7х + 21), а также вынесение семерки за скобки:
(2х – 5)(х + 3) = 7х + 21
(2х – 5)(х + 3) – 7х + 21 = 0
(2х – 5)(х + 3) – 7(х + 3) = 0
У нас появился бином, оба одночлена которого имеют общий множитель (х + 3), который выносится за скобки, образуя произведение полиномов:
(2х – 5)(х + 3) – 7(х + 3) = 0
(х + 3)(2х – 5 – 7) = 0
(х + 3)(2х – 12) = 0
Решая элементарное вычитание в скобках, мы пришли к простому произведению с нулевым результатом; теперь можно решить систему уравнений:
(х + 3)( 2х – 12) = 0
х + 3= 0
х = -3
2х -12 = 0
2х = 12
х = 6
Ответ: корнями уравнения являются числа -3 и 6.
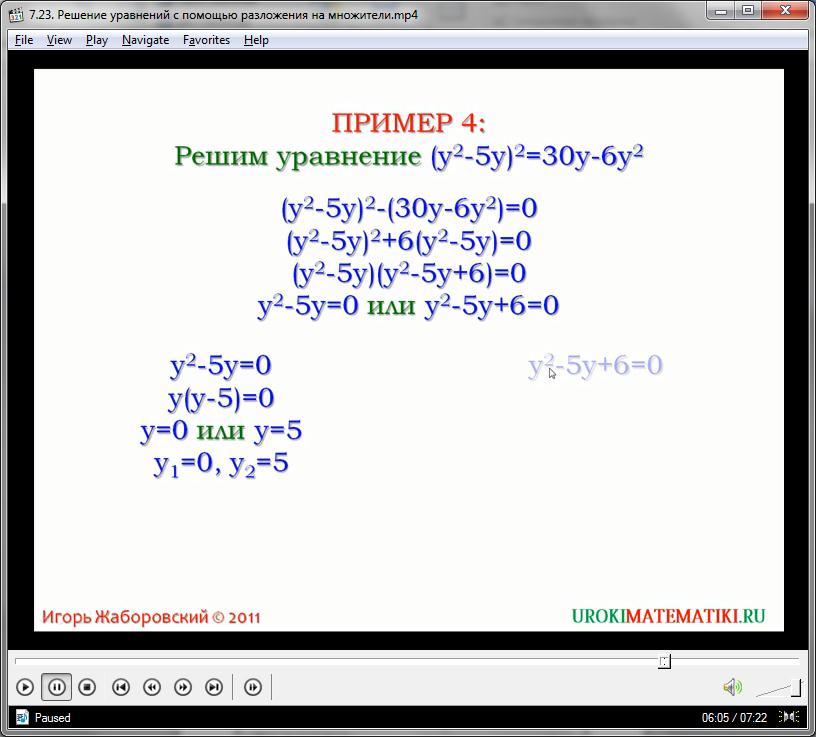
Большинство уравнений, которые изначально имеют приравнивание к нулю или которые могут быть преобразованы до подобного вида, в итоговом варианте сводятся к системе двух (иногда больше) уравнений. И очень часто ответами являются два корня. Только в случае степенных переменных корни могут быть отброшены по причине недействительности.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 16152 |
| Номер материала | 465 |