
Урок "Вычисления. Доказательство тождеств"

Краткое описание документа:
В прошлых видеоуроках мы рассмотрели основные приемы преобразования многочленов, которые базируются на вынесении общего множителя за скобки. В более сложном варианте необходима группировка одночленов, имеющих схожее основание для создания нескольких многочленов, связанных операцией произведения. Оба способа имеют множество вариаций в исполнении, которые особенно хорошо проявляются в сложных многочленах. Это позволяет использовать процедуру преобразования полиномов для решения многих задач смежных тем.
В новом видео мы рассмотрим возможные расчеты при решении нетривиальных задач. В этом будем использовать навыки преобразования полиномов по типу вынесения множителя.
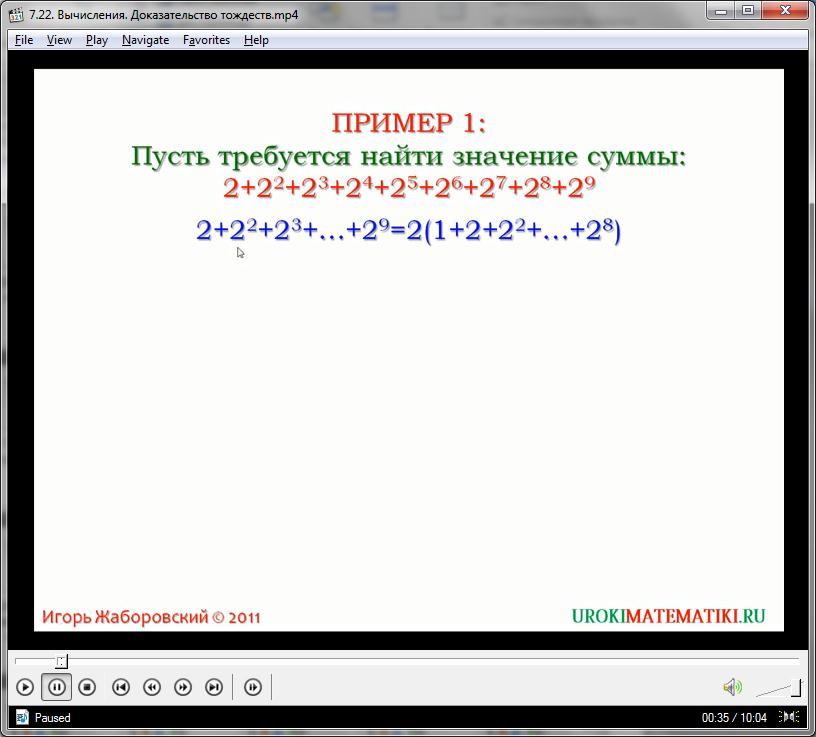
Рассмотрим следующий пример. Нам нужно найти сумму выражения:
2 + 22 + 23 + …+29
Для того чтобы преобразовать данный многочлен, вынесем двойку за скобки:
2 + 22 + 23 + …+29 = 2(1 + 2 +…28)
Теперь необходимо задать переменную х, которая будет равна выражению в скобках, не включающих единицу. Используем переменную для обеих частей равенства:
2 + 22 + 23 + …+29 = 2(1 + 2 +…28)
х = (2 +…28)
х + 29 = 2(1 + х)
Таким образом, мы получили уравнение с одной неизвестной, которое представляет собой равенство двух многочленов. Решаем уравнение, раскрывая скобки умножением и соблюдая правила переноса знаков:
х + 29 = 2(1 + х)
х + 29 = 2 + 2х
29 – 2 = 2х – х
х = 29 – 2
Легко понять, что искомая сумма представляет собой х + 29 поэтому можно записать следующим образом:
2 + 22 + 23 + …+29 = х + 29 = 29 – 2 + 29 = 2(29) -2 = 2(512) – 2 = 1022
Итак, вместо прямого возведения каждой двойки в соответствующую степень (этот процесс растянется на восемь действий) с последующим суммированием, мы значительно упростили задачу, преобразовав исходный многочлен в уравнение (при помощи метода введения мнимой неизвестной) и развязав его.
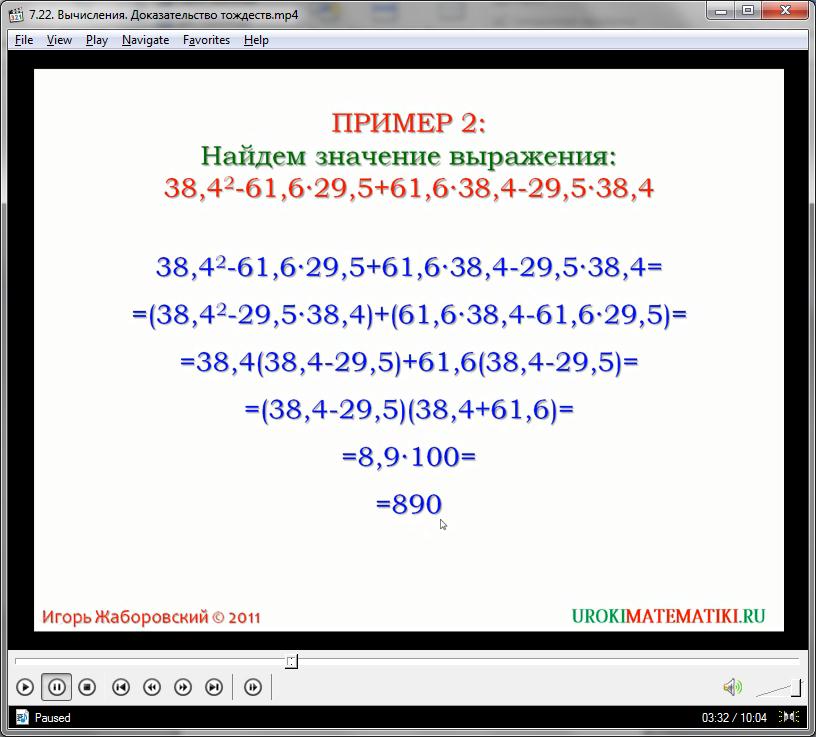
Рассмотрим второй пример. Найти значение выражения:
38,42 – 61,6*29,5 + 61,6*38,4 – 29,5*38,4
Выражение в примере перегружено дробными числами, а также имеет достаточно много одночленов. Но при этом легко подметить наличие некоторых общих оснований, по которым можно сгруппировать многочлен. Возьмем за основу первой группы – 38,4 а за основу второй – 61,6. Группируем в первую часть первый и четвертый одночлен, во вторую часть – второй и третий одночлен:
38,42 – 61,6*29,5 + 61,6*38,4 – 29,5*38,4 =
= 38,4(38,4– 29,5) + 61,6(38,4 – 29,5)
Как мы видим, после группировки у нас получились две одинаковые скобки в общем выражении. Выносим выражение в скобках, как общий множитель, за пределы выражения, производим вычисления внутри скобок, получаем ответ:
38,4(38,4– 29,5) + 61,6(38,4 – 29,5) =
= (38,4– 29,5)(61,6 + 38,4) = 8,9 * 100 = 890
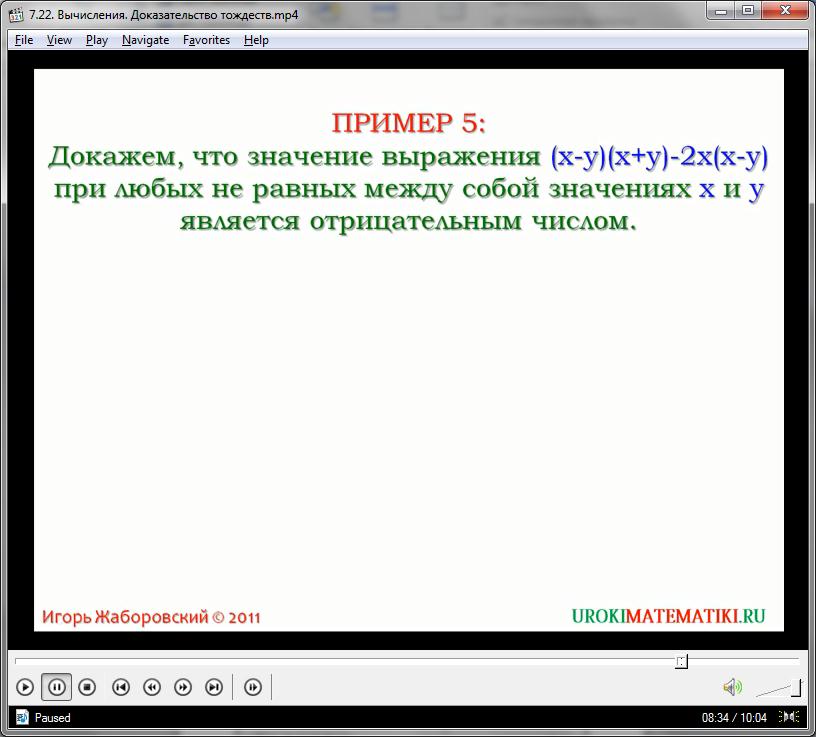
Стоит отметить, что буквенные варианты подобных произведений многочленов – например, (х – у)(х + у) – являются стандартами во многих вычислениях. Расчеты этих выражений, выполненные по правилам перекрестного умножения, именуются формулами сокращенного умножения; в дальнейших видеоуроках мы изучим эту тему более подробно.
Рассмотрим ещё один пример. Нам необходимо доказать, что выражение вида 814 – 97 + 312 кратно 73. В этом выражении нет явных общих множителей, но есть способ найти подходящую основу. Все числовые коэффициенты в многочлене кратны трем. Преобразуем числа, как степени тройки:
814 – 97 + 312 = (34)4 – (32)7 + (3)12
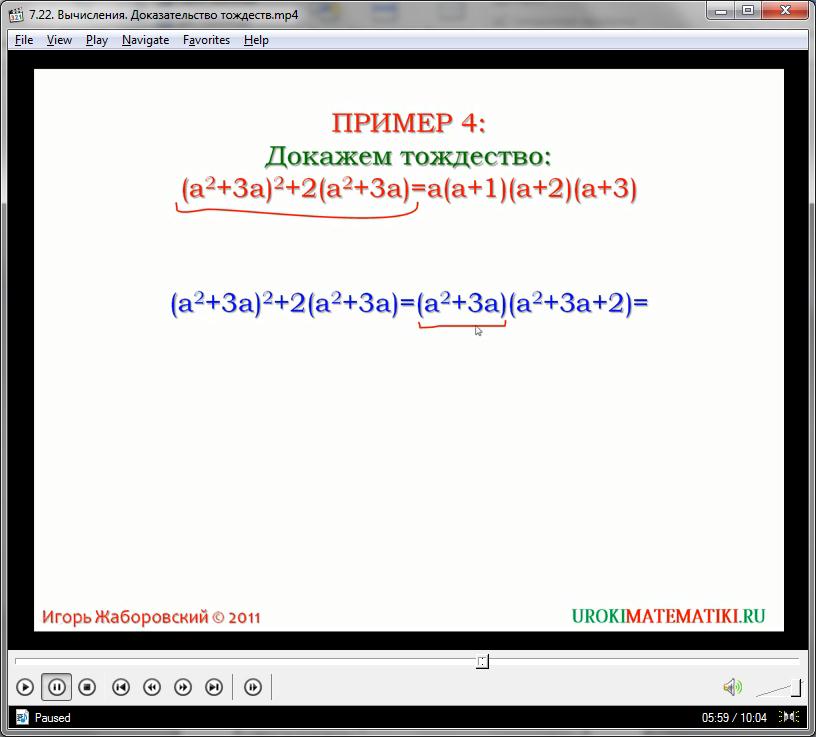
Согласно правилу степеней, центральный элемент под скобками повышает свою степень путем произведения со значением, стоящим за скобками, так что:
(34)4 – (32)7 + (3)12 = 316 – 314 + 312
Получаем новый многочлен, который можно преобразовать на основании 312. Решая выражение в скобках, имеющее достаточно малые степени, получим:
316 – 314 + 312 = 312(34 – 32 + 1) = 312(81 – 9 + 1) = 312(73)
Итоговое выражение состоит из двух множителей, один из которых равен 73, а второй является целым натуральным числом (так как основание степенного выражения равно целому значению). Поэтому, все выражение кратно числу 73.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 3919 |
| Номер материала | 455 |