
Урок "Алгоритм решения рационального уравнения"

Краткое описание документа:
Алгебраические уравнения представляют собой важную составляющую современной алгебры. Уравнения существуют многих видов, так как существует много разнообразных методов их решения. В этом видеоуроке рассматривается алгоритм решения именно рациональных уравнений.

Этот алгоритм наиболее простой и самый распространенный на практике.Прежде всего здесь чётко описаны понятия «рациональное выражение» и «рациональное уравнение», что является приравниванием рационального выражения к нулю.Самым распространенным определением рационального уравнения является представление его как равенство двух рациональных выражений. Что касается самого алгоритма решения рационального уравнения, то он достаточно доступно разъяснён в видеоролике на примере решения двух уравнений.
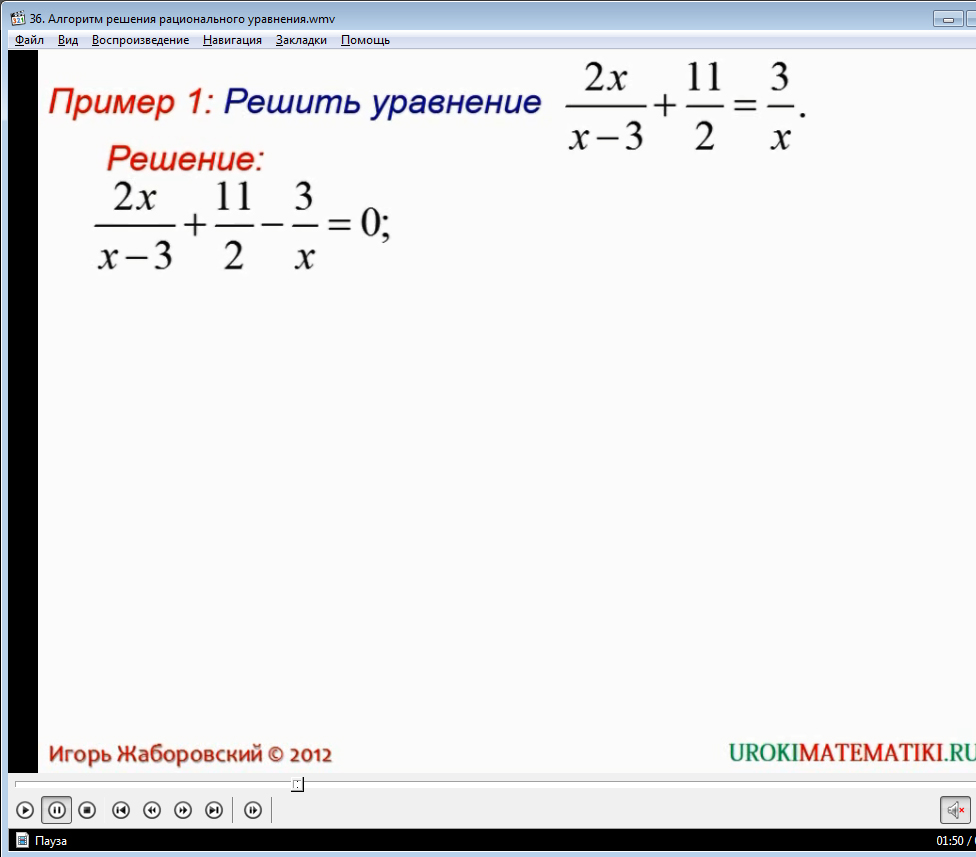
После теоретического вступления рассматривают пример №1. Здесь правую часть уравнения переносят в левую часть с противоположным знаком, и всё рациональное выражение, образовавшийся в правой части, приравнивают к нулю. За этим проводятся не сложные алгебраические действия в выражении, что приводит к получению выражения вида p(x)/q(x). Эта дробь приравнивается к нулю. То есть, таким образом, из исходного рационального уравнения получают уравнение вида p(x)/q(x)=0. Далее, как видно из видео, упоминается условие равенства дроби нулю.
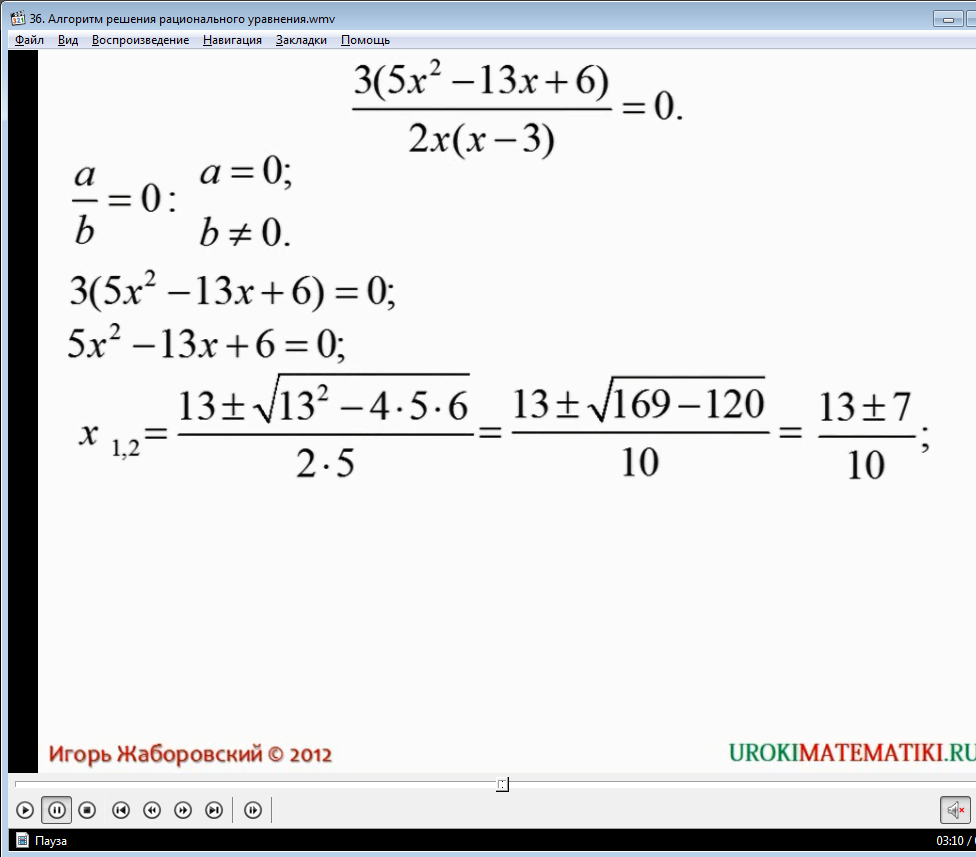
А именно - это равенство правильное, тогда и только тогда, когда числитель дроби равный нулю, а знаменатель нулю не равен. Следовательно, p(x) = 0 и q(x) не равно 0. Далее решается первое уравнение обычным алгебраическим способом, что приводит к получению двух корней. В видеоуроке сказано, что обязательным этапом алгоритма является также проверка условия q(x) не равно 0. Аналогично решается данное уравнение и проверяется, совпадают ли корни этого уравнения с корнями уравнения p(x) = 0. В данном примере одинаковых решений нет. Из видеоролика понятно, что решение уравнения являются решениями исходного уравнения, представленного в примере №1. На протяжении всего процесса решения заданного рационального уравнения используются методы решения квадратных и линейных уравнений, которые известны из предыдущих уроков.После приведённого примера крайне понятно изложен алгоритм решения рационального уравнения, что состоит из четырех шагов, которые легко запоминаются:

- Перенести все выражения в одну из частей уравнения.
- Преобразовать полученное в одной части выражение к виду алгебраической дроби.
- Приравнять дробь к нулю и решить уравнение, которое после этого получено.
- Приравнять числитель дроби к нулю и проверить,удовлетворяют ли корни этого уравнения условие q(x) не равно 0. Если так, то эти корни и являются корнями заданного уравнения, если нет - это сторонние корни, и их включение в результат невозможно.
Для закрепления метода в видеоуроке приведён ещё один пример, где, как видим, ещё раз отдельно, на практике, выделяется каждый из четырех шагов алгоритма. Что касается примера №2, то следует заметить, что здесь рассматривается случай, когда решения уравнений p(x) равно 0 и q(x) не равно 0 частично совпадают. Именно в этой части видеоурока вводится понятие «посторонний корень». Из видеоурока понятно, что такие корни исключаются из перечня корней исходного рационального уравнения.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5543 |
| Номер материала | 560 |