
Урок "Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a"

Краткое описание документа:
Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.
В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = – 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x1 + πk. Значение x1 – это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от –π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.
По аналогии решается уравнение tg x = – 3. По построенным графикам функций y = tg x и y = – 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x2 + πk. С помощью арктангенса решение можно записать как x = arctg (– 3) + πk. На следующем рисунке увидим, что arctg (– 3) = – arctg 3.

Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от –π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.
Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от –π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от –π/2 до π/2.
Пример 2 – вычислить арктангенс отрицательного числа. Используя равенство arctg (– a) = – arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от –π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, -– tg x = – π/3. Ответом уравнения будет – π/3.
Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.
Пример 4: вычислить tg x = – 4,1. В данном случае x = arctg (– 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (– 4,1) + πk.
В примере 5 рассматривается решение неравенства tg x > 1. Для решения построим графики функций y = tg x и y = 1. Как видно на рисунке, эти графики пересекаются в точках x = π/4 + πk. Т.к. в данном случае tg x > 1, на графике выделим область тангенсоиды, которая находится выше графика y = 1, где x принадлежит интервалу от π/4 до π/2. Ответ запишем как π/4 + πk < x < π/2 + πk.
Далее рассмотрим уравнение ctg x = a. На рисунке изображены графики функций у = ctg x, y = a, y = – a, которые имеют множество точек пересечения. Решения можно записать как x = x1 + πk, где x1 = arcctg a и x = x2 + πk, где x2 = arcctg (– a). Отмечено, что x2 = π – x1. Из этого следует равенство arcctg (– a) = π – arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
В конце видеоурока делается еще один важный вывод – выражение ctg x = a можно записать в виде tg x = 1/a, при условии, что a не равно нулю.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим решение уравнений tg х = 3 и tg х= - 3. Решая первое уравнение графически, мы видим, что графики функций у = tg х и у = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде
х = х1 + πk, где х1 – это абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение
arctg 3 (арктангенс трех).
Как же понимать arctg 3?
Это число, тангенс которого равен 3 и это число принадлежит интервалу (- ; ). Тогда все корни уравнения tg х = 3 можно записать формулой х = arctg 3+πk.
Аналогично решение уравнения tg х = - 3 можно записать в виде х = х2 + πk, где х2 – это абсцисса точки пересечения прямой у = - 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение arctg(–3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= - arctg 3.
Сформулируем определение арктангенса. Арктангенсом а называется такое число из промежутка (–;), тангенс которого равен а.
Часто используют равенство: arctg(-а) = -arctg а, которое справедливо для любого а.
Зная определение арктангенса, сделаем общий вывод о решении уравнения
tg х= a: уравнение tg х = a имеет решение х = arctg а + πk.
Рассмотрим примеры.
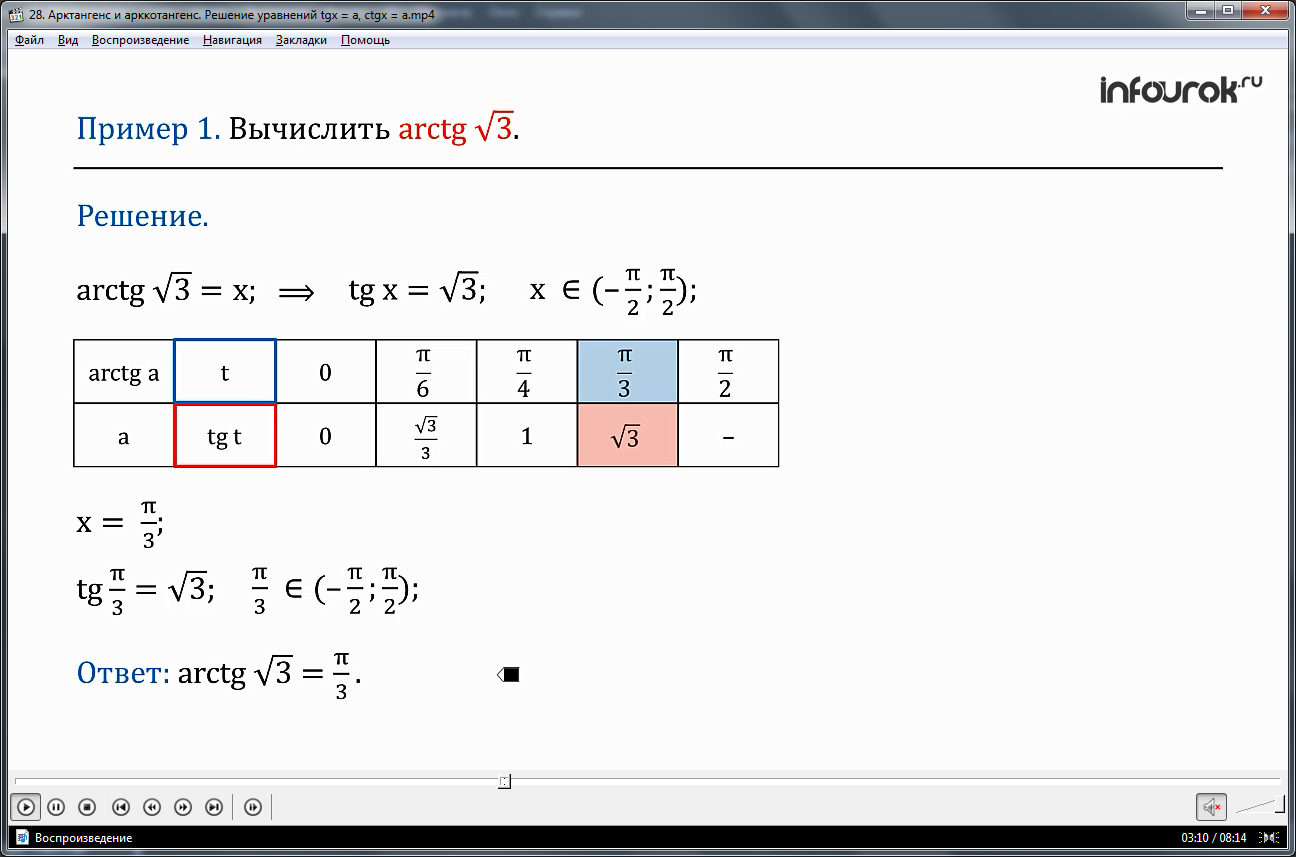
ПРИМЕР 1.Вычислить arctg.
Решение. Пусть arctg = х, тогда tgх = и хϵ (- ; ). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ; ).
Итак, arctg =.
ПРИМЕР 2. Вычислить arctg (- ).
Решение. Используя равенство arctg( - а) = - arctg а, запишем :
arctg(- ) = - arctg . Пусть - arctg = х, тогда - tgх = и хϵ (- ; ). Следовательно, х =, так как tg = и ϵ (- ; ). Показать таблицу значений
Значит - arctg=- tgх= - .
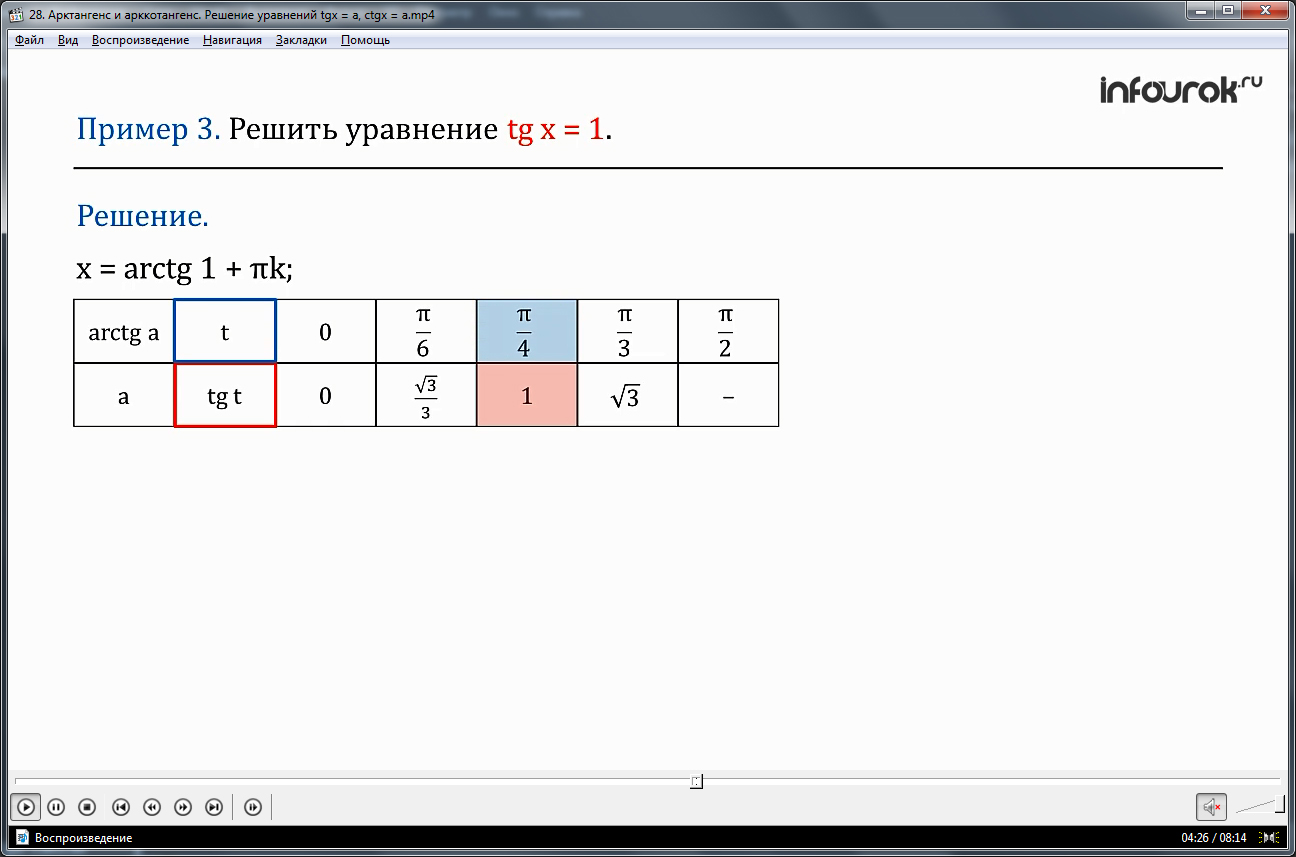
ПРИМЕР 3. Решить уравнение tgх = 1.
Решение.
1. Запишем формулу решений: х = arctg 1 + πk.
2. Найдем значение арктангенса
так как tg = . Показать таблицу значений
Значит arctg1= .
3. Поставим найденное значение в формулу решений:
х = + πk.
ПРИМЕР 4. Решить уравнение tgх = - 4,1( тангенс икс равно минус четыре целые одна десятая).
Решение. Запишем формулу решений: х = arctg ( - 4,1) + πk.
Вычислить значение арктангенса мы не можем, поэтому решение уравнения оставим в полученном виде.
ПРИМЕР 5. Решить неравенство tgх 1.
Решение. Будем решать графически.
- Построим тангенсоиду
у= tgх и прямую у = 1(рис.2). Они пересекаются в точках вида х = + πk.
2. Выделим промежуток оси икс, на котором главная ветвь тангенсоиды расположена выше прямой у = 1, так как по условию tgх 1. Это интервал (; ).
3. Используем периодичность функции.
Своийство 2. у=tg х – периодическая функция с основным периодом π.
Учитывая периодичность функции у= tgх, запишем ответ:
( ; ). Ответ можно записать в виде двойного неравенства:
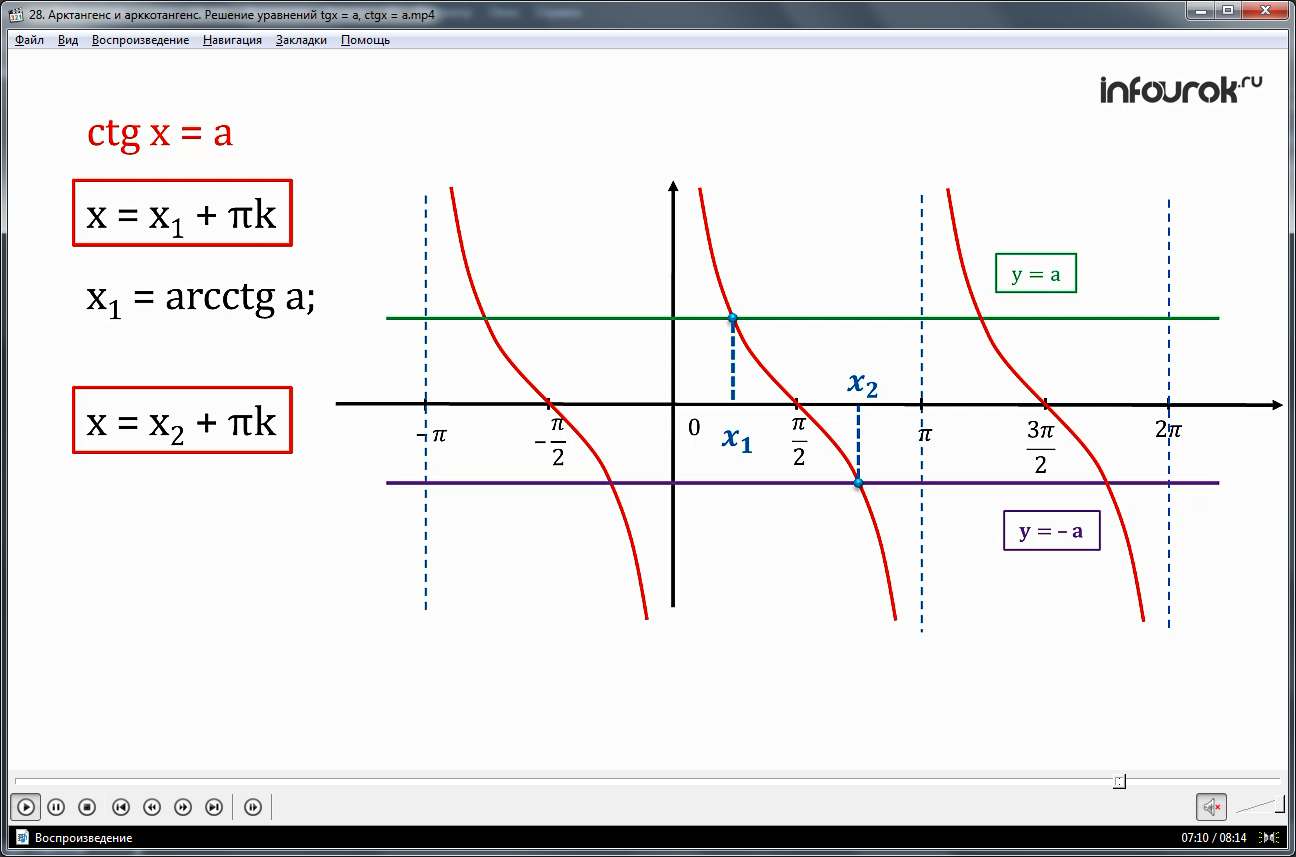
Перейдем к уравнению ctg х = a. Представим графическую иллюстрацию решения уравнения для положительного и отрицательного а (рис.3).
Графики функций у= ctg х и у =а а также
у= ctg х и у=-а
имеют бесконечно много общих точек, абсциссы которых имеют вид:
х = х1 + , где х1 – это абсцисса точки пересечения прямой у =а с главной ветвью тангенсоиды и
х1 = arcсtg а;
х = х2 + , где х2 – это абсцисса точки пересечения прямой
у = - а с главной ветвью тангенсоиды и х2 = arcсtg (- а).
Заметим, что х2 = π - х1. Значит, запишем важное равенство:
arcсtg (-а) = π - arcсtg а.
Сформулируем определение: арккотангенсом а называется такое число из интервала (0;π), котангенс которого равен а.
Решение уравнения ctg х = a записываются в виде: х = arcсtg а + .
Обратим внимание, что уравнение ctg х = a можно преобразовать к виду
tg х = , за исключение, когда а = 0.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 17363 |
| Номер материала | 856 |