
Урок «Целое уравнение и его корни»

Краткое описание документа:
Видеоурок «Целое уравнение и его корни» дает представление о целом уравнении, видах таких уравнений, приведении уравнения к стандартному виду, решении подобных уравнений. Задача данного видеоурока – облегчить усвоение материала по данной теме, формировать умения решать задания, в которых используются целые уравнения, способствовать запоминанию учебного материала.
Оформление наглядного материала в виде урока дает возможность заменить учителя в части подачи стандартного блока нового материала, освободить учителя для углубления индивидуальной работы. Видеоматериал помогает сконцентрировать внимание учащихся на освоении нового материала, помогает глубже его понять и лучше запомнить.

Видеоурок начинается с представления темы урока. На экране отображается определение целого уравнения, содержащего одну переменную, как уравнения, обе части которого представляют собой целые выражения. Ниже приведены примеры таких уравнений: (х5-2)2+х3=х10-3(х-2), х3(х3-36)=2(х+8)-2. Далее рассматривается преобразование уравнений, при котором все его слагаемые переносятся из правой части в левую, раскрываются скобки и приводятся подобные слагаемые. После этого уравнение принимает вид, в котором левая его часть представляет собой многочлен, а правой части – 0. Отмечается, что в ходе преобразований получается уравнение, равносильное данному. К тому же уравнение, к которому приведено исходное, в общем виде можно записать: Р(х)=0, где Р(х) – многочлен стандартного вида.
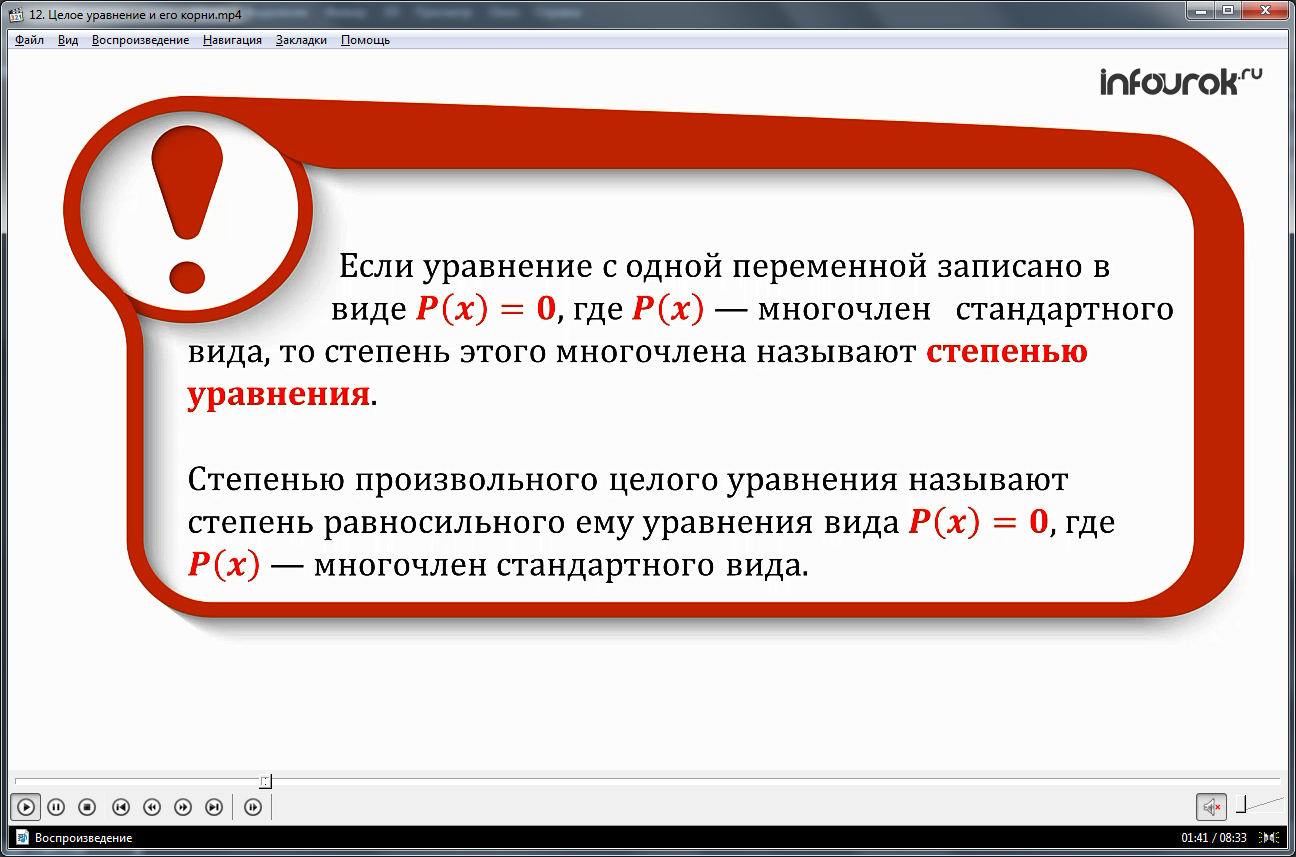
Рассмотренные примеры подводят к общему выводу о том, что любое целое уравнение, содержащее одну переменную, может быть приведено к виду Р(х)=0, где Р(х) – многочлен, степень которого является степенью данного уравнения. То есть степень некоторого произвольного целого уравнения может быть определена после приведения его к равносильному уравнению вида Р(х)=0 и равна степени многочлена Р(х).
Далее рассматривается уравнение первой степени – такое уравнение, которое приводится к виду ах+b=0 с одной переменной х, числами а и b, при этом а≠0. Корень данного уравнения находится по формулех=-b/a. Отмечается, что такое уравнение имеет один корень.
Также предлагается рассмотреть решение уравнения второй степени, которое приводится к виду ах2+bx+c=0, содержащее переменную х, некоторые числа а, b, c, при этом а≠0. Известен способ нахождения корней данного уравнения путем вычисления дискриминанта. На экране отображается формула нахождения дискриминанта для уравнения второй степени: D=b2-4ac. В зависимости от значения дискриминанта, может быть два корня уравнения – D>0, один – для D=0, или корни отсутствуют D<0. Напоминается формула для нахождения корней уравнения второй степени при положительном или нулевом дискриминанте: х=(-b+-√D)/2a.
Ученикам представляются также уравнения третьей и четвертой степени, которые приводятся к видам ах3+bx2+cх+d=0 и ах4+bx3+cх2+dх+e=0. В каждом из этих уравнений имеется одна переменная х, коэффициент при старшей степени a≠0, остальные коэффициенты – некоторые числа. Уточняется, что уравнение третьей степени не может иметь более трех корней, а уравнение четвертой степени имеет не более четырех корней. В качестве дополнительной информации ученикам сообщается, что формулы для нахождения корней уравнений третьей и четвертой степени существуют, но они громоздкие и неудобные в применении, а для уравнений пятой степени и выше формул для нахождения корней не существует. Однако решить такие уравнения иногда удается при помощи специальных приемов, которые позволяют упростить выражение и найти корни.

На примере демонстрируется один из способов, как можно найти корни уравнения, не применяя сложных формул нахождения корней.Описывается, каким образом решение некоторых уравнений можно найти с помощью разложения многочлена на множители. Уравнение х3-27x2-х+27=0 раскладывается на множители, выведя за скобки общий множитель (х-27). В результате преобразований получим произведение (х-27)(х-1)(х+1)=0 Полученное уравнение сводится к нахождению решений трех уравнений х-27, х-1, х+1. Из этих уравнений легко найти корни х1=27, х2=1, х3=-1.
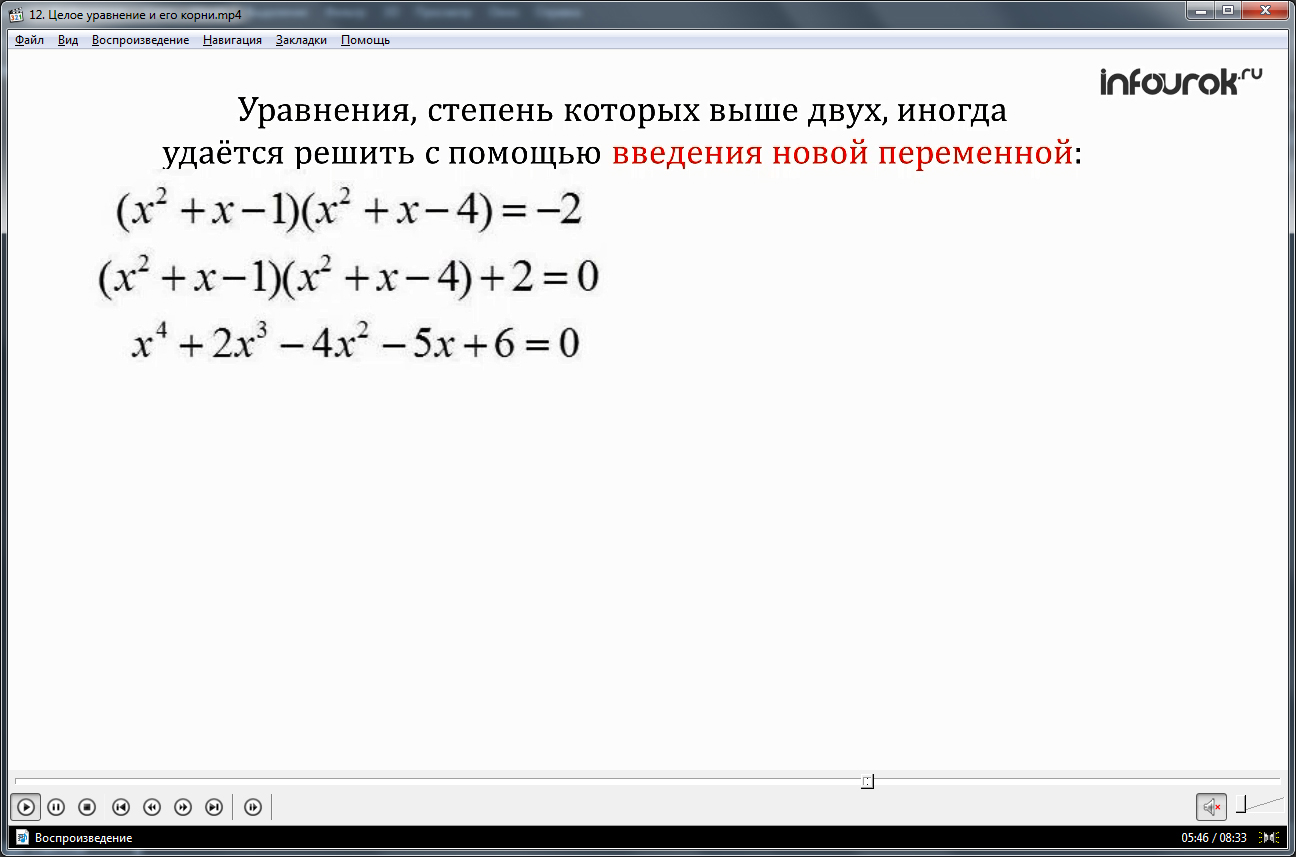
Далее рассматривается еще один способ решения уравнений высокой степени – способ введения новой переменной. Применение способа описывается на примере решения уравнения (х2+х-1)(х2+х-4)=-2. Сначала все члены уравнения переносятся в левую часть, раскрываются скобки. После данный преобразований получается многочлен стандартного вида 4 степени. Однако, подметив особенность данного уравнения – то, что в исходном уравнении есть одинаковые части х2+х, вводим новую переменную для обозначения этого выражения: х2+х=у. после подстановки новой переменной в уравнение, получим уравнение вида (у-1)(у-4)=-2. После приведения уравнения к стандартному виду получается обычное квадратное уравнение, корнями которого будут у1=2, у2=3. Значение корней у подставим в выражение для определения значения искомых х. Нахождение корней уравнения сводится к решению двух уравнений х2+х=2 и х2+х=3. В результате вычислений будут найдены корни данных уравнений будут х1=1, х2=-2, х3≈1,3, х4≈-2,3. Отмечается, что данным способом нередко решают уравнения четвертой степени вида ax4+bx2+c=0, в которых х является переменной, a, b, c – некоторыми числами, где а≠0. На экране дается определение биквадратного уравнения как уравнения четвертой степени вида ax4+bx2+c=0са≠0.
Для закрепления полученных знаний о решении уравнений способом введения новых переменных предлагается рассмотреть решение биквадратного уравнения 16х4-8х2+1=0. Вводится новая переменная у=х2. После ее введения образуется квадратное уравнение, имеющее один корень у=0,25. После подстановки значение новой переменной в выражение для ее определения можно найти корни уравнения х1=0,5 и х2=-0,5.
Видеоурок«Целое уравнение и его корни» подробно и наглядно представляет учащимся материал по данной теме, поэтому может быть использован учителем не только на уроке в школе, но также при дистанционном обучении, рекомендуется для самостоятельного освоения темы.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9285 |
| Номер материала | 659 |