
Урок «Число е. Функция у=ех, ее свойства, график, дифференцирование»

Краткое описание документа:
Тема: Число e. Функция <!--?mso-application progid="Word.Document"?--> 14y=ex"> , ее свойства, график, дифференцирование
Для изучения темы вспомним, как расположен график показательной функции в прямоугольной системе координат. Для примера построим графики функций <!--?mso-application progid="Word.Document"?--> 14y=2x">
Для построения найдем координаты нескольких точек графика. Построим этот график.
Вспомним особенности расположения графика показательной функции в прямоугольной системе координат.
- График показательной функции проходит через точку (0; 1)
- График имеет горизонтальную асимптоту <!--?mso-application progid="Word.Document"?--> 14y=0"> при х→+∞
- График обращен выпуклостью вверх
- В каждой точке к графику функции можно привести касательную

Для примера построим касательную к графику функции в точке х=0. В данный момент это построение может быть сделано примерно. На графике выглядеть это будет так.
Аналогично можно построить касательную к графику функции <!--?mso-application progid="Word.Document"?--> 14y=3x"> в точке х=0.
Следует отметить, что касательные в данной точке расположены примерно одинаково и отличаются только углом наклона прямой к положительной части оси Х.
Угол наклона касательной функции
<!--?mso-application progid="Word.Document"?--> 14y=2x"> примерно равен 35°, а угол наклона касательной функции <!--?mso-application progid="Word.Document"?--> 14y=3x"> примерно равен 48 градусов. Учеными проверено, что если увеличить основание с 3 до 10, то градусная мера угла изменится до 66, 5 градусов. Значит, логично предположить, что существует положение касательной функции при котором угол наклона касательной будет равен 45 градусам.
Возникает вопрос: Какое основание должно быть у показательной функции при таком положении касательной.
Учеными же доказано, что такое основание существует и оно равно иррациональному числу 2,7182818284590…. . Данное число принято обозначать буквой <!--?mso-application progid="Word.Document"?--> 14e"> и брать его приблизительное значение 2,7
График функции <!--?mso-application progid="Word.Document"?--> 14y=Рµx"> это экспонента, отличающаяся от других экспонет тем, что угол между касательной к графику в точке х=0 и осью абсцисс равен 45°.
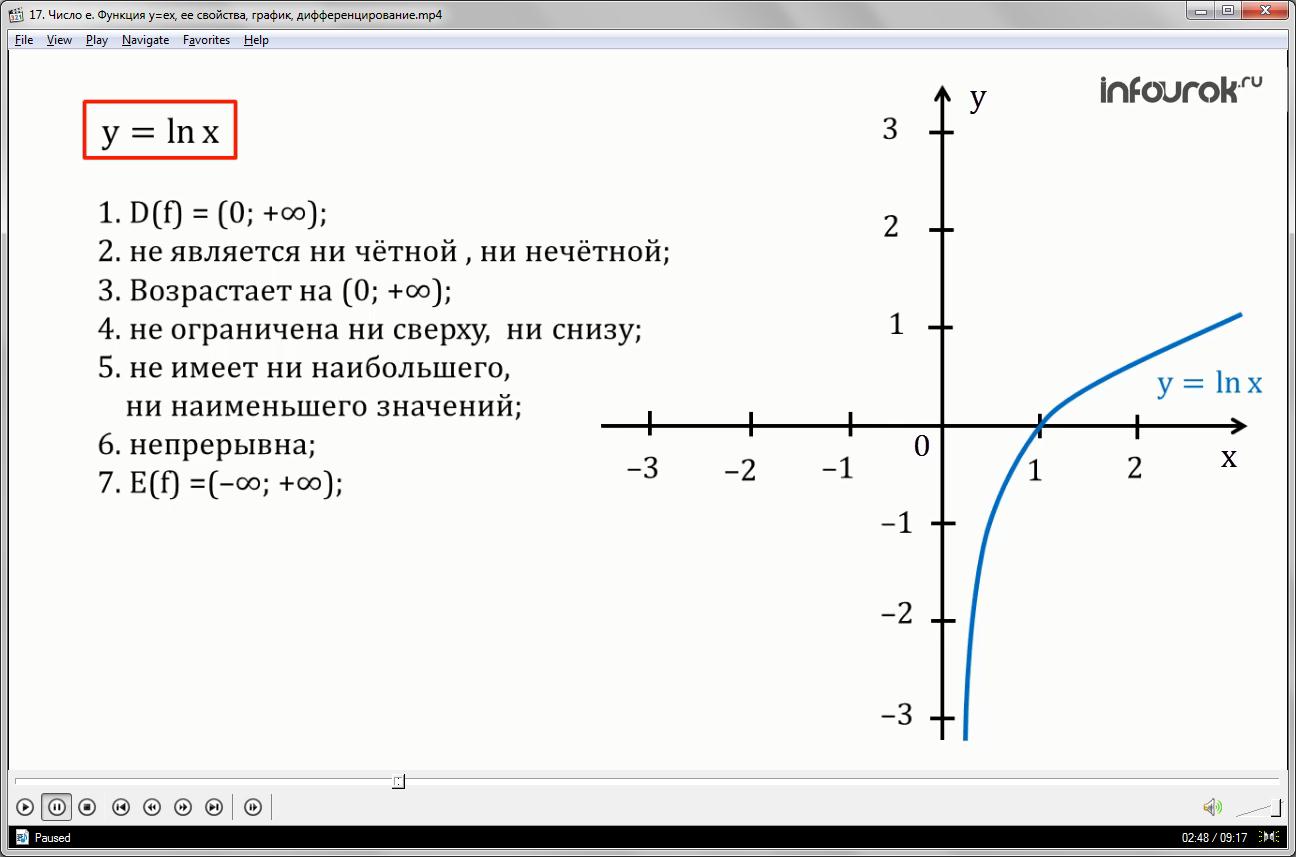
Рассмотрим свойства функции
Далее нужно прочитать свойства с правого столбика
Следует отметить, тот факт, что функция <!--?mso-application progid="Word.Document"?--> 14y=Рµx"> имеет касательную в точке х=0, а уравнение касательной составляется через нахождение производной функции, то очевидно для функции <!--?mso-application progid="Word.Document"?--> 14y=Рµx"> также существует производная функция. А функция <!--?mso-application progid="Word.Document"?--> 14y=Рµx"> дифференцируема.
Очевидно не только то что функция
дифференцируема, а даже известно
значение её производной функции в
точке х=0.
Вспомним, что значение производной
функции в точке равно значению
тангенса угла наклона касательной в
данной точке к оси х. В нашем случае
угол равен 45 градусам, значит тангенс
этого угла равен 1, что означает, что
значение производной в точке х=0
также равно 1.
Это выполнимо если производная
функции <!--?mso-application progid="Word.Document"?--> 14y=Рµx"> равна <!--?mso-application progid="Word.Document"?--> 14Рµx"> . Проверим это.
Напомним, что уравнение касательной
к графику функции f(x) в точке
<!--?mso-application progid="Word.Document"?--> 14x0=a">
имеет вид <!--?mso-application progid="Word.Document"?--> 14y=fa+f,(a)(x-a)"> .
Так как, а=0. Тогда f(а)= f(0) =1.
Производная функции равна <!--?mso-application progid="Word.Document"?--> 14Рµx"> <!--?mso-application progid="Word.Document"?--> 14,"> а её
значение в точке равно 1. Составим
уравнение касательной, для этого
подставим в уравнение найденные
значения. Получим y=1+1(x-0)=1+x-0=1+x .
Таким образом уравнение касательной
к графику функции <!--?mso-application progid="Word.Document"?--> 14y=Рµx"> в точке x=0
равно y=x+1 .
Уравнение касательной подтверждает
сделанные предположения.
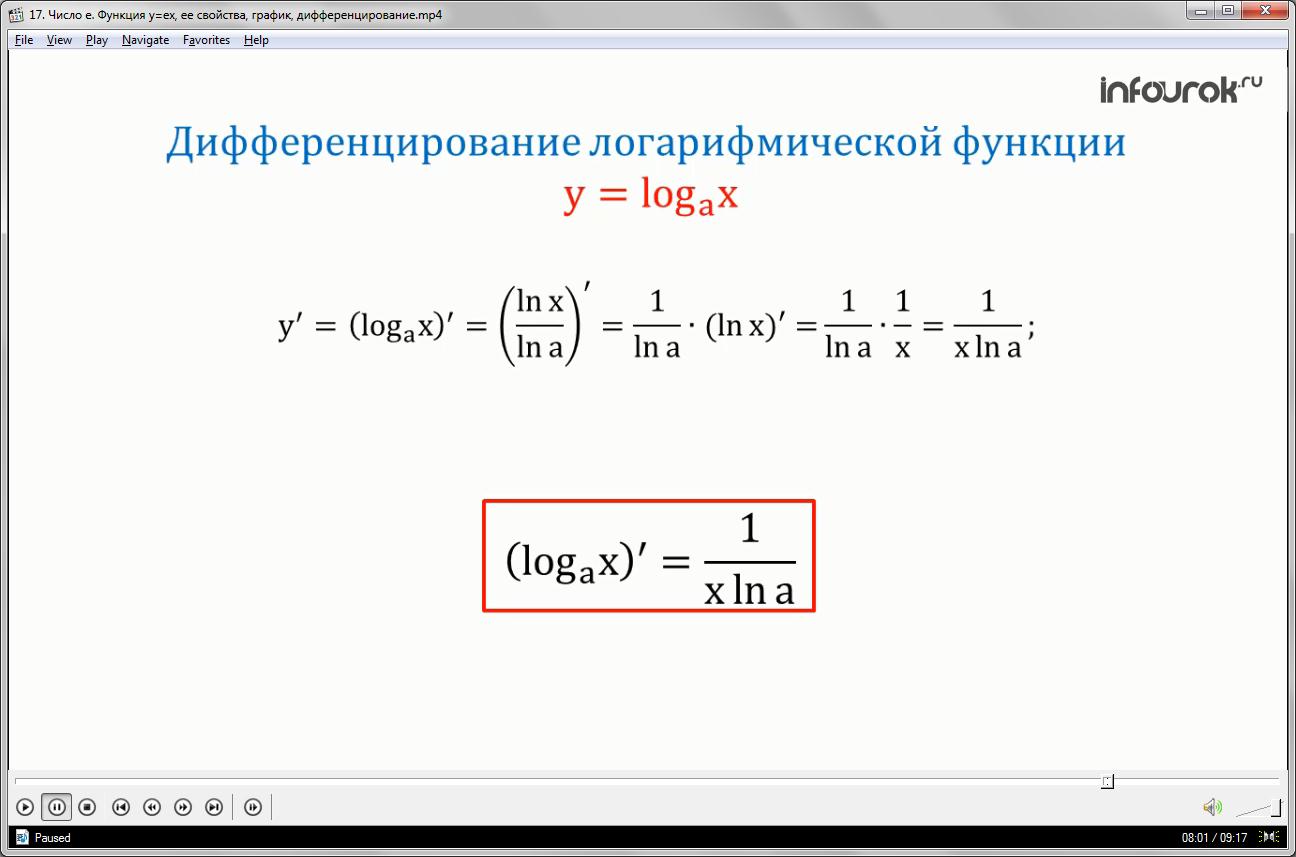
Таким образом. В <!--?mso-application progid="Word.Document"?--> 14(ex),=ex"> . В
действительности же чаще
используется формула

Рассмотрим действие данных формул
на примере
Пример 1.Вычислить значение
производной <!--?mso-application progid="Word.Document"?--> 14y=ex2-4"> в точке x=2.
Для решения воспользуемся правилом
дифференцирования сложной функции f’(g(x))=f’(g(x))∙g’(x)
Получим:
<!--?mso-application progid="Word.Document"?--> 14y=(ex2-4)'=(x2-4)'в€™ (ex2-4)'=2xв€™ex2-4">
Производная от <!--?mso-application progid="Word.Document"?--> 14(x2-4)"> равна 2x , а производная от <!--?mso-application progid="Word.Document"?--> 14ex2-4"> равна <!--?mso-application progid="Word.Document"?--> 14ex2-4"> .
Запишем это в виде произведения 2х и
Для нахождения значения производной,
подставим вместо х число 2. Е в
нулевой степени — это единица. Значит,
значение производной будет равно 4.
Пример 2. Промежутки убывания
функции <!--?mso-application progid="Word.Document"?--> 14y=x2 в€™ex">
Воспользуемся уже известным
алгоритмом отыскания у наименьшего
и у наибольшего .
1) Найдём производную функции
воспользуемся правилом
(f(x)∙g(x ))’=f(x)’g(x)+g(x)’∙f(x) .
Тогда <!--?mso-application progid="Word.Document"?--> 14y'=x2в€™ex'=(x2)'ex"> + <!--?mso-application progid="Word.Document"?--> 14ex'x2=2xв€™ex+exв€™x2=xex(2+x)">
Эта производная существует при всех
значениях х, значит критических точек
у функции нет.
2)Найдём нули производной функции.
Уравнение <!--?mso-application progid="Word.Document"?--> 14xex2+x=0"> имеет корни если хотя бы один из множителей равен нулю, а другой при этом не потеряет
смысла. Разделим уравнение на три
новых уравнения . Уравнение не имеет корней. Тогда корни уравнения 0 и -2 будут стационарными точками,
отметим их на координатной прямой.
Производная на полученных
промежутках чередует знаки начиная с плюса слева на право. Значит на
отрезке от -2 до 0 функция
<!--?mso-application progid="Word.Document"?--> 14y=x2 в€™ex">
Число e участвует в описании многих
математических процессов и мы ещё
встретимся с ним . так же широко число
используется и для описания процессов
в экономике , физике…
В экономическом смысле число e
означает максимально возможную
годовую прибыль при 100 % годовых и максимальной частоте капитализации процентов.
В ряду иррациональных чисел число е
стоит перед известным всем числом.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6296 |
| Номер материала | 1066 |