
Урок "Числовые последовательности"

Краткое описание документа:
Тригонометрия, как отдельный раздел, изучается в 10 классе, наряду с остальными. Она содержит в себе большое количество тем, которые будут изучать все новые формулы, без которых невозможно представить себе решение тех или иных практических примеров.
Некоторые тригонометрические выражения станут более понятными и простыми в случае их грамотного упрощения. Для этого необходимо понять, когда и какую формулу необходимо применить. Чтобы появились подобные навыки, нужно разобрать теорию.
Необходимость уметь справляться с числовыми последовательностями разного типа может появиться при выполнении различных заданий и задач па разным наукам. Множество натуральных чисел является само по себе числовой последовательностью. С этого начинается демонстрация данного видеоурока. Диктор объясняет, каким образом можно записать данную последовательность, обозначения выводятся на экран вместе с теорией.
Практически любую последовательность можно задать словесно, при выводе правила его задания будут использованы исключительно слова. При этом формулы не будут использованы. Приводится пример такой последовательности, которая включает в себя упорядоченные от меньшего до большего простых чисел.
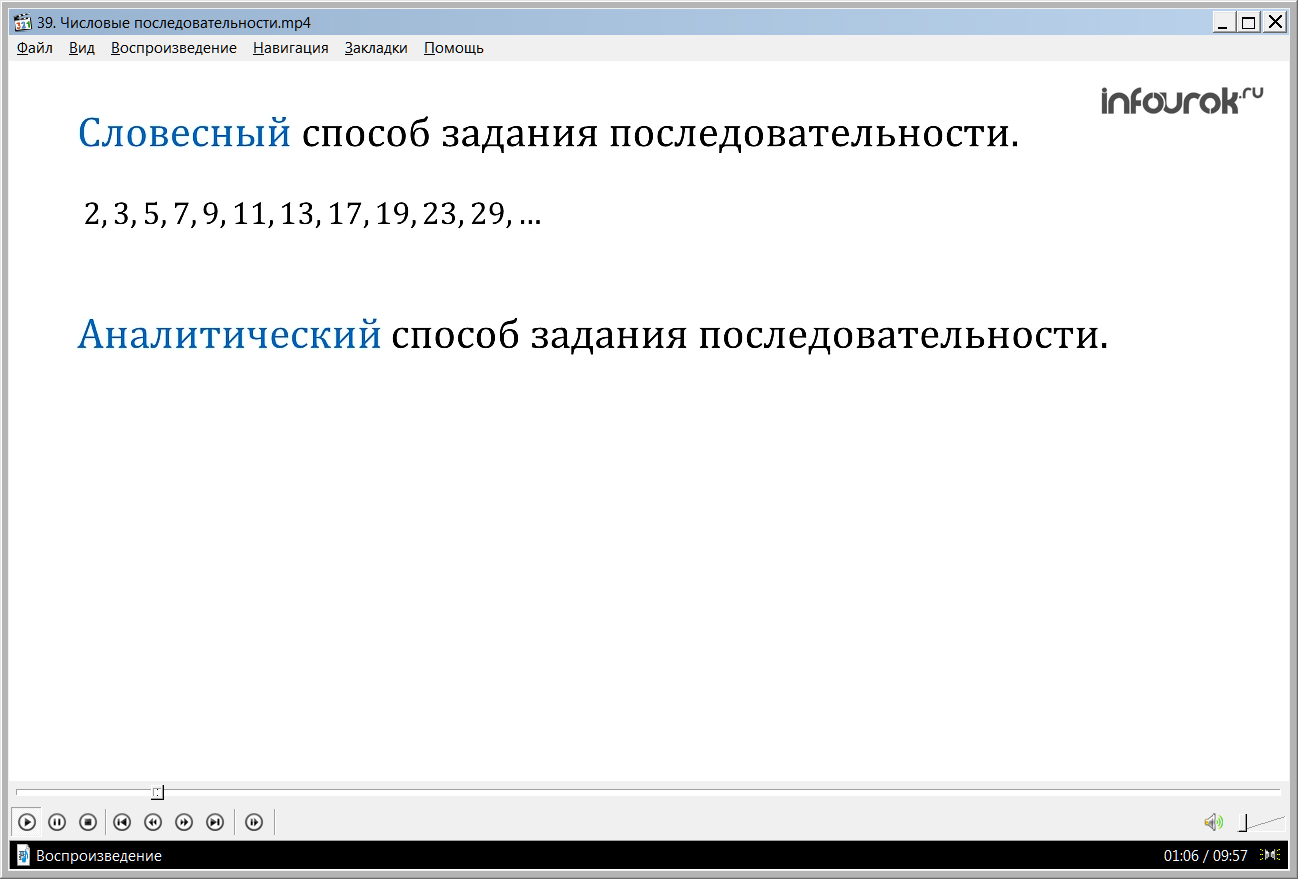
Есть еще один довольно распространенный вид задания некоторой последовательности – аналитический. При этом записывается формула энного члена, с помощью которого можно найти любой иной член последовательности.
Приводятся два примера. Второй случай из них представляет собой некоторую последовательность, где каждый член равняется константе С. Как мы видим, элементы последовательности могу являться равными друг другу.
На этом способы, с помощью которых можно задать последовательности, не заканчиваются. Есть еще один метод, который называется рекуррентным. В отличие тот аналитического метода задания последовательности, в данном случае, для того, чтобы найти некоторый элемент, необходимо знать обо всех предыдущих.
Классическим примером рекурсивной последовательности, является арифметическая. Она изучалась в более младших классах, на ряду с геометрической, которая задается аналогичным образом. Невозможно найти последующий элемент, не зная значения предыдущих.
Каждая последовательность может быть рассмотрена с точки зрения монотонности и ограниченности. Если изучать некоторую последовательность, то нужно учесть, что она может быть ограничена либо сверху, либо снизу. Если некоторый элемент последовательности больше, без исключений, всех остальных, то такая последовательность однозначно будет называться ограниченной сверху. И наоборот, если существует некоторый член последовательности, при котором все остальные значение больше него, то такая последовательность будет называться ограниченной снизу. Если же последовательно является ограниченной и сверху, и снизу, то она называется ограниченной последовательностью.
При изучении этих определений в видеоуроке, несомненно, приводятся примеры. С помощью них школьники могут как можно глубже понять суть определений.
Приводится пример и ограниченной последовательности, которая имеет наибольшее и наименьшее значения. Это объясняется и графически на координатной плоскости путем построения графика.
В каком же случае последовательность будет возрастающей? Если каждый последующий член некоторой последовательности будет больше предыдущей, то она будет считаться возрастающей, и наоборот, если каждый последующий элемент меньше предыдущей, то она будет называться убывающей. Убывающая или возрастающая последовательность называется монотонной. Чтобы этого наглядно увидеть, лучше всего продемонстрировать школьникам геометрически.
В видеоуроке приводятся очень хорошие примеры, которые закрепят в памяти те или иные определение и свойства последовательностей.
Стоит отметить, что последовательность может быть ни возрастающей, ни убывающей. Для ясности приводится пример.
Данный видеоурок содержит и теоретическую, и практическую часть, которые сопровождаются спокойным и понятным голосом диктора. При этом текст составлен профессионалами. Он выводится на экран удобным цветом и шрифтом и понятен для уровня 10-классников. Материал соответствует учебному плану и не содержит ненужной информации.
ТЕКСТОВАЯ РАСШИФРОВКА:
Определение 1. Функцию вида у = f(x), xN (игрек равно эф от их, икс принадлежит множеству натуральных чисел) называют функцией натурального аргумента или числовой последовательностью и обозначают у=f(n) (игрек равно эф от эн) или у1, у2, у3, …, уn,... ((игрек первый, игрек второй, игрек третий и так далее игрек энный и так далее)
Иногда для обозначения последовательности используется запись (уn) (игрек энный).
Первый способ задания последовательности словесный, когда правило задания последовательности описано словами, без указания каких-то формул.
Например, (последовательность простых чисел):
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ... (два, три, пять, семь, одиннадцать, …)

Второй способ задания последовательности аналитический, то есть указывают формулу ее n-го члена (энного члена).
Приведем примеры.
Пример.
1) уn =n3.(игрек энный равен эн в третей степени) Это — аналитическое задание последовательности 1, 8, 27, 64, ... ,n3, ...
Нетрудно найти член последовательности с соответствующим номером, для этого достаточно указать конкретное значение n (эн). Если, например, n =9, то у9 =93,(игрек девятый равен девять в кубе) т.е. у9 =729 (игрек девятый равен 729). Напротив, если взят определенный член последовательности, можно указать его номер. Например, если уn =1331 (игрек энный равен 1331), то из уравнения n3 =1331 (эп в третей степени равно 1331) находим, что
n =11. Это значит, что 11-й (одиннадцатый) член последовательности равен 1331.
2) уn =С. (игрек энный равен цэ). Задана последовательность вида С, С, С, .... С,...
Она называется постоянной (или стационарной).
Третий способ задания последовательности рекуррентный: задают правило, позволяющее вычислить n-й член последовательности через предшествующий, его отличие от аналитического в том, что бы найти n-й (энный) член последовательности надо знать все предыдущие.
Пример.
1)арифметическая прогрессия — это числовая последовательность (аn), заданная рекуррентно соотношениями: a1 =а, аn+1=аn+d (a и d — заданные числа, d — разность арифметической прогрессии).
2) Геометрическая прогрессия — это числовая последовательность (bn) (бэ энное), заданная рекуррентно соотношениями: b1=b, bn+1 =bn·q
(b и q — заданные числа, b0, q0; q — знаменатель геометрической прогрессии). Эти прогрессии вы изучали в средней школе.
2. Свойства числовых последовательностей
Числовую последовательность можно рассматривать как частный случай числовой функции, значит она обладает некоторыми свойствами функций, например, ограниченностью и монотонностью.
Определение 2. Последовательность (уn) (игрек энный)называют ограниченной сверху, если все ее члены не больше некоторого числа.
То есть, последовательность (уn) (игрек энный)ограничена сверху, если существует число М (эм большое) такое, что для любого n выполняется неравенство уnМ. (игрек энный меньше или равен эм большое) Число М называют верхней границей последовательности.
Например, последовательность –1, –8, –27, –64, ... , –n3 , ... ограничена сверху. В качестве верхней границы можно взять число М= –1 (эм большое равно минус единица) или любое число, которое больше, чем –1, например 0.
Определение 3. Последовательность (уn) (игрек энный)называют ограниченной снизу, если все ее члены не меньше некоторого числа.
То есть, последовательность (уn) (игрек энный)ограничена снизу, если существует число т (эм малое) такое, что для любого n(эн) выполняется неравенство уnт (игрек энный больше или равен эм малое). Число т (эм малое) называют нижней границей последовательности.
Пример.
последовательность 0, 1, 2, 3, 4, ..., (n–1), ... ограничена снизу. В качестве нижней границы можно взять число т=0 или любое число меньше 0.
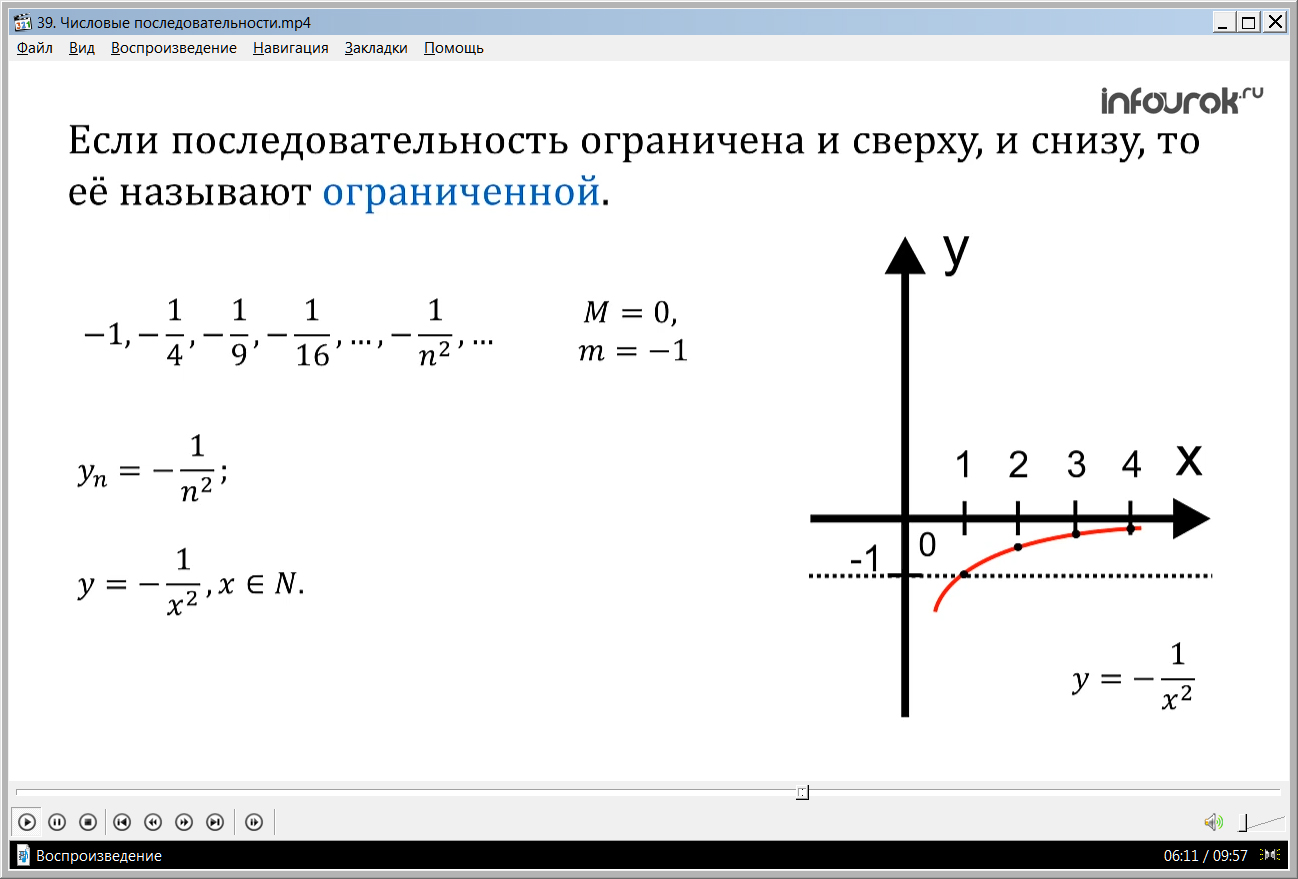
Если последовательность ограничена и сверху, и снизу, то ее называют ограниченной.
Пример.
–1, , , , ... , , ...Эта последовательность ограничена и сверху, и снизу. В качестве верхней границы можно взять число М=0, в качестве нижней границы – число m= –1.
Если построить график последовательности уn = – (игрек энный равный минус единица деленная на эн в квадрате), т.е. график функции y = –, xN, (игрек равный минус единица, деленная на икс в квадрате, где икс принадлежит множеству натуральных чисел эн), в прямоугольной системе координат, то окажется, что весь он расположен в полосе между некоторыми горизонтальными прямыми, например, у=0, и у=–1 (рис. 1), а в этом и состоит, геометрический признак ограниченности функции.
Рис. 1
Если члены последовательности отметить точками на числовой прямой, будет наглядно видно свойство ограниченности последовательности,. Ограниченность последовательности означает, что все члены последовательности (точнее, соответствующие им точки прямой) принадлежат некоторому отрезку. Так, изобразив члены последовательности уn = точками на числовой прямой, замечаем, что все они принадлежат отрезку [–1; 0] как показано на рисунке 2.
Рис. 2
Определение 4. Последовательность (уn) (игрек энный) называют возрастающей, если каждый ее член больше предыдущего:
y1< y2 < y3 < … < yn < yn+1 < …(игрек первый меньше игрек второго меньше игрек третьего меньше и так далее меньше игрек энного меньше игрек эн плюс первого и так далее).
Пример:
1, 3, 5, 7, … , 2n–1, ... – возрастающая последовательность.
Так как 1<3<5<7<…<2n-1<2(n+1)–1<…
Определение 5. Последовательность (уn) называют убывающей, если каждый ее член меньше предыдущего: y1> y2 > y3 > y4 > … > yn > yn+1 > …(игрек первый больше игрек второго больше игрек третьего больше и так далее больше игрек энного больше игрек эн плюс первого и так далее)
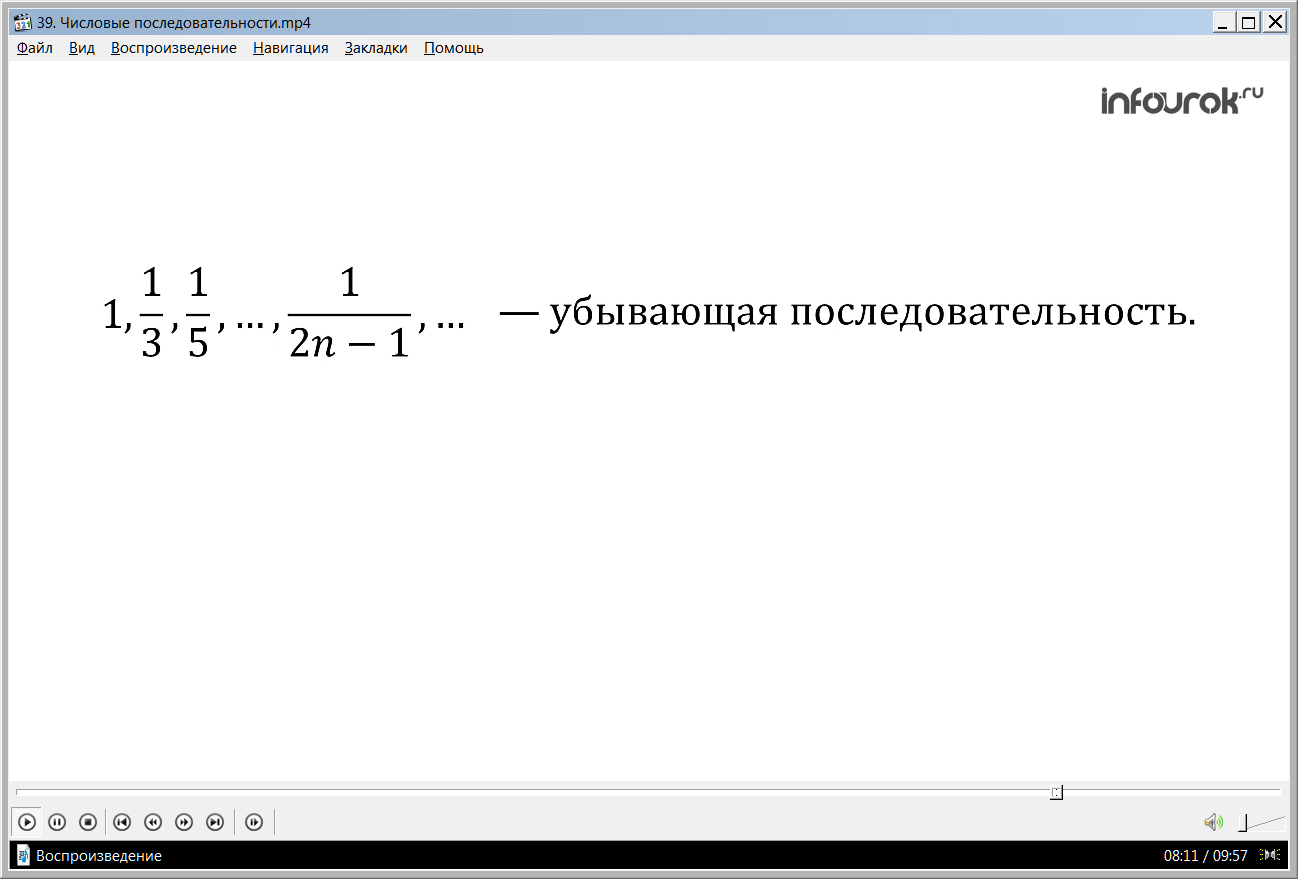
Пример:
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Приведем еще несколько примеров.
1) –1, 2 ,–3, 4, ... , (–1)n·n, ...Эта последовательность не является ни возрастающей, ни убывающей (немонотонная последовательность).
2) уn =3n(игрек энный равен три в степени эн). Речь идет о последовательности 3, 9, 27, 81, 243, ... Это — возрастающая последовательность.
Вообще, еслиa > 1, то последовательность уn =аn возрастает.
3) yn = ()n( игрек энный равен одной пятой в степени эн). Речь идет о последовательности , , , , .... Это — убывающая последовательность.
Вообще, если 0 < a < 1, то последовательность уn =аn убывает.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7299 |
| Номер материала | 862 |