
Урок "Что такое функция"

Краткое описание документа:
Функция – это одно из наиболее фундаментальных понятий линейной алгебры, способствующее обособлению целого раздела математики, посвященного различным множественным зависимостям. Кроме того, именно функциями являются тысячи формул, которые используются в самых разных отраслях науки и техники.
Прежде чем приступить к изучению всего многообразия функций, следует основательно усвоить, что же представляет это понятие. В данном уроке мы рассмотрим теоретические основы зависимостей между группами математических множеств.
Любой обширный массив действительных чисел принято называть множеством. Множества могут включать различные элементы, но чаще всего это некий набор чисел. При этом числа необязательно идут по порядку и могут иметь достаточно сложную систему взаимных связей, либо же вообще быть несвязанными.
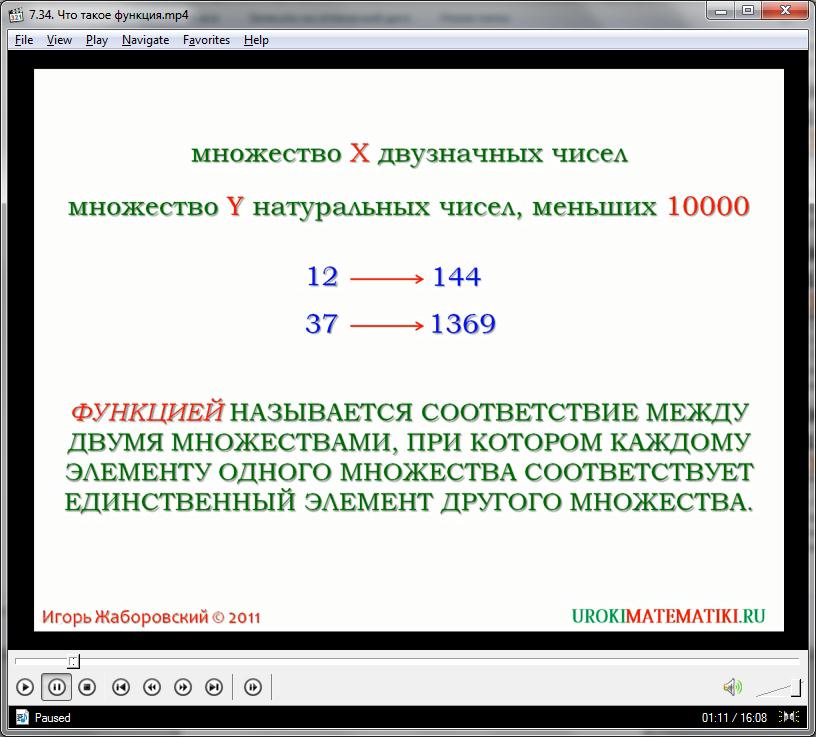
Предположим, существует некое множество чисел, каждое из которых мы обозначим как абстрактную х. Пределы множества могут уходить в бесконечность, хотя очень часто они все же ограничиваются формулами. Возведем в квадрат каждый элемент множества х. Как результат, мы получим второе множество, состоящее из х2. Обозначим числа нового множества как у. Вполне очевидно, что множество у будет подобным множеству х – они напрямую связаны определенной зависимостью. Более того, эту зависимость легко выразить, ведь любой элемент второго множества равен:
у = х2
Каждый член множества х строго соответствует определенному члену множества у и наоборот. Соответствие выражается некой математической формулой, которая и формирует второе множество на основании первого. Строгую математическую зависимость между числами двух множеств х и у называют функцией:
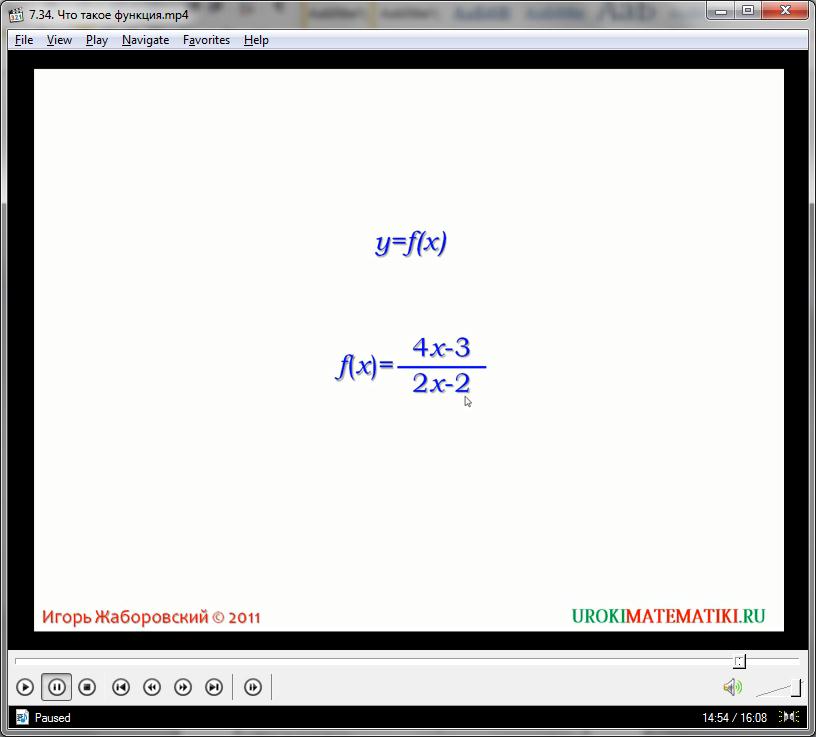
у = f(х)
В линейной записи функция именуется аналитической. Зависимость между х и у может принимать любые допустимые алгебраические формулы, образуя, таким образом, практически неисчерпаемое поле различных взаимосвязанных пар множеств. Общая стандартизированная формула для отображения функции, имеющая вид:
у = f(х)
Содержит обязательные элементы – у (зависимая переменная, которая формируется функцией), х (аргумент функции, число, которое обрабатывается в процессе вычислений), и f() – саму функцию, как математическую формулу зависимости.
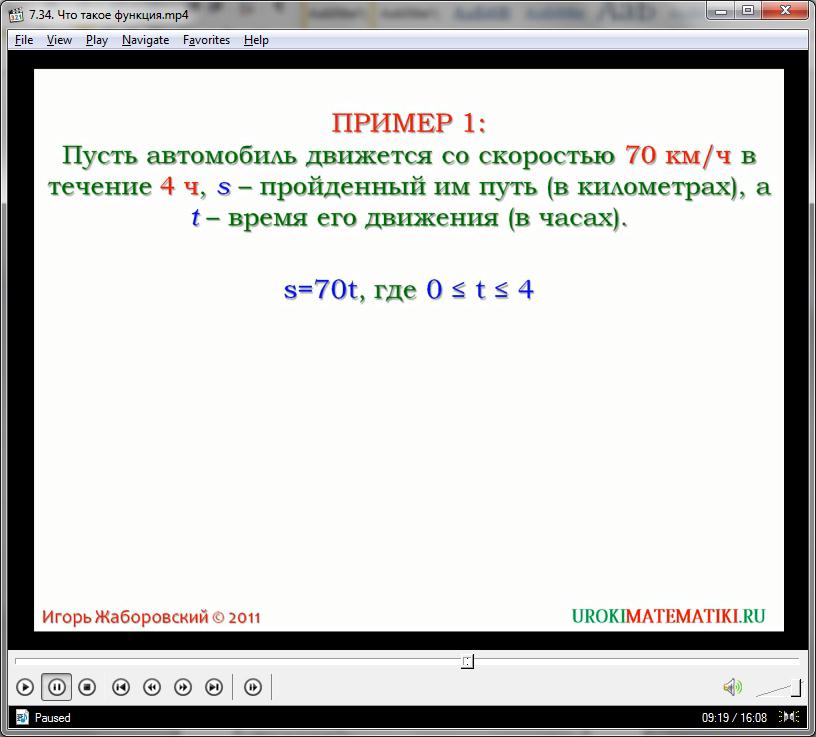
Как уже упоминалось в нашем видео, множества чисел, которые участвуют в создании функции, иногда могут быть ограничены самой математической формулой. Изначально в функции общего вида у = f(х) подразумевается, что оба множества являются бесконечными, включая абсолютно все действительные числа. Далеe из-за функциональных ограничений могут появиться некоторые пределы. В силу этого каждая функция обладает своим полем выбора чисел. Все действительные числа множества х, которые соответствуют формуле, лежат в так называемой области определения функции. С другой стороны, множество чисел у, зависимых от х, лежит в области значений функции. Рассмотрим те случаи, когда данные области не совпадают со всем бесконечным множеством чисел.
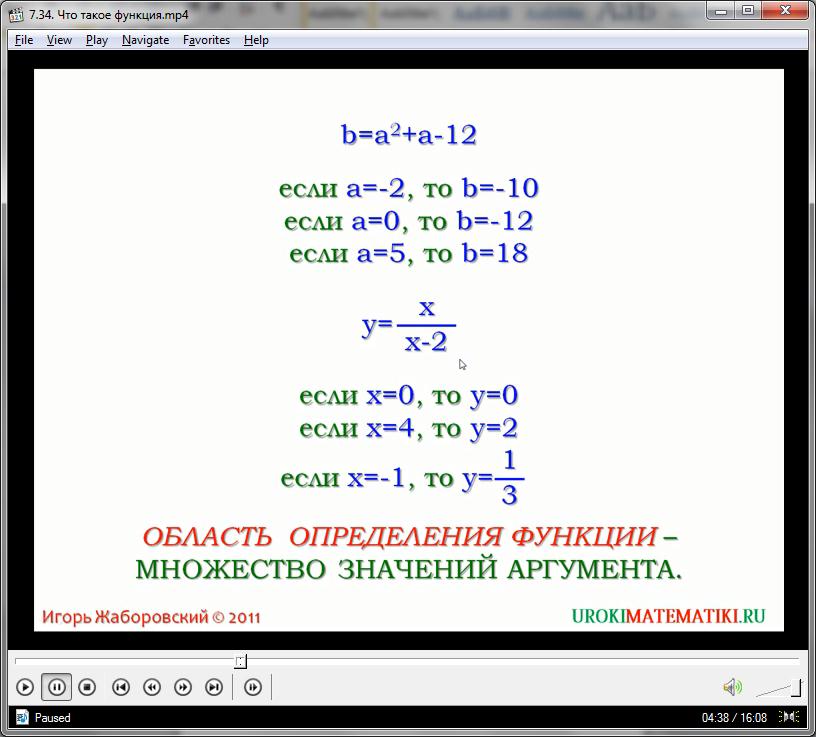
У нас есть функция вида:
у = х/(х-2)
Как известно, ноль не может выступать делителем, и при обнулении нижней части дроби всё выражение теряет свой смысл. Поэтому (х-2) не может быть равным нулю. Соответственно, х не может быть равным двум, иначе функция лишится смысла. Таким образом, область определения данной функции лежит на всем множестве чисел, исключая число «2». Иначе говоря, функция прерывается в данной точке (точнее, прерывается её график).
Рассмотрим второй пример. Дана функция вида:
у = |х|
Модуль любого числа всегда положителен. Поэтому при любом значении х зависимая переменная будет положительной. Иначе говоря, область значений у лежит исключительно в положительной части множества действительных чисел.
Подавляющее большинство функций в математике задается посредством чисел, математических операторов и двух переменных – х и у. Подобные функции именуются числовыми. Помимо них существуют и нечисловые зависимости. Например, каждой точке координационной декартовой сетки соответствует лишь одно число х и одно число у. Подобная связь так же именуется функциональной зависимостью, хоть и невыражаемой в формульном (аналитическом) виде.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5495 |
| Номер материала | 461 |