
Урок "Разложение на множители разности n-х степеней"

Краткое описание документа:
Формулы сокращенного умножения – это очень удобный инструмент для операций с многочленами. Как правило, это позволяет сократить сложные конструкции полиномов до небольшого выражения, представляемого двучленом. Либо же,в ином порядке – из произведения двух многочленов легко выводится компактный бином.
Такие действия бывают необходимыми при решении тривиальных уравнений и неравенств, а также при различных доказательных задачах.
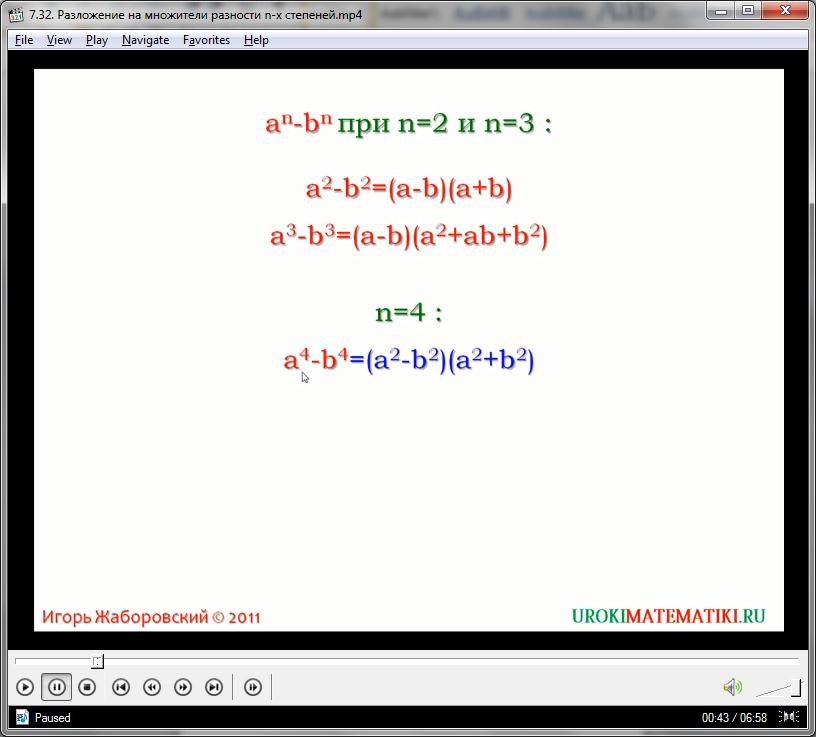
В прошлых видеоуроках мы рассмотрели формулы разности квадратов и разности кубов. Попытаемся вывести формулу ещё более высокого порядка – найдем, чему равна разность выражений в четвертой степени:
х4 – у4
Это выражение сравнительно легко преобразовать, подставив вместо х4 и у4 идентичные квадратные выражения (х2)2 и (у2)2:
х4 – у4 = (х2)2 – (у2)2
В итоге мы получаем разность квадратов, которую можно представить при помощи элементарной ФСУ как:
(х2)2 – (у2)2 = (х2 + у2)(х2 – у2)
С другой стороны, вторые скобки полученного выражения содержат разность квадратов, которую можно легко преобразовать:
(х2 + у2)(х2 – у2) = (х2 + у2)((х + у)(х - у))
Отсюда следует, что:
х4 – у4 = (х2 + у2)(х + у)(х – у)
Оставим основополагающую общую часть (х - у), остальные два выражения в скобках перемножим:
х4 – у4 = (х2 + у2)(х + у)(х – у) = (х – у)(х3 + х2у + ху2 + у3)
Для чего необходимо выделять (х – у), будет показано позже. Итак, мы нашли ещё одну формулу для разности степенных выражений. Это равенство достаточно сложно для выражения – однако стоит понимать, что оно вполне логично вписывается в ряд подобных формул для определения разности квадратов и кубов. Сравним эти формулы между собой, для того, что бы найти общие закономерности:
х2 – у2 = (х – у)(х + у)
х3 – у3 = (х – у)(х2 + 2ху + у2)
х4 – у4 = (х – у)(х3 + х2у + ху2 + у3)
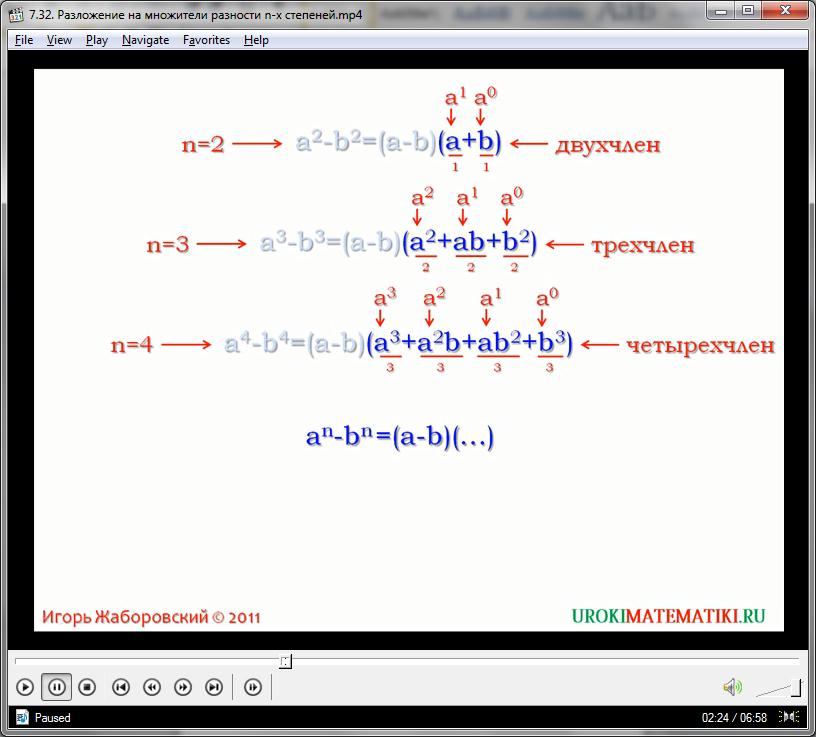
На видео четко представлено, что разности переменных в различной степени имеют некоторые закономерности. Все выражения по правую сторону равенства состоят из произведения двух многочленов, причем один из них всегда имеет форму х – у (изначальная разность выражений). Второй же образован неким сложным полиномом, количество одночленов которого растет со степенью.
Для выведения общей формулы, которая поможет преобразовать в произведение полиномов разность переменных с любой степенью, важно понять общие тенденции в равенствах начального порядка. Заметим, что второй многочлен в нашем произведении представляет собой сумму попарных произведений двух выражений. Причем степени переменных находятся в обратной взаимосвязи. Чтобы было легче понять эти закономерности, перепишем равенство для разности выражений четвертой степени таким образом:
х4 – у4 = (х – у)(х3у0 + х2у1 + х1у2 + х0у3)
Любое число в нулевой степени обязательно равно единице. Поэтому к любой реальной переменной можно смело дописывать конструкцию с нулевой степенью. Помним так же, что любая переменная имеет степень – если она не указана, то равна единице. Эти правила обращения со степенями и позволили представить равенство в более понятном виде.
Обратим внимание, что количество членов в многочлене вторых скобок равно основной степени (которую имеют переменные в разности). По ряду многочлена, степень одного выражения алгебраически убывает, а степень второго – прибывает. При этом крайними точками для степеней являются 0 и старшая степень начальной разности выражений.
Пользуясь этими соображениями, выведем формулу для нахождения разности выражений пятой степени:
х5 – у5 = (х – у)(х4у0 + х3у1 + х2у2 + х1у3 + х0у4)
Для начала, мы прописываем первый множитель (х – у) без изменений. Второй же многочлен будет представлять сумму пяти элементов (по старшей степени). Элементы, в свою очередь, образованы произведением переменных с алгебраическим, обратным и взаимосвязанным изменением степеней. В многочлене:
х4у0 + х3у1 + х2у2 + х1у3 + х0у4
х понижает степень с 4 до 0, у повышает с 0 до 4. Для самопроверки полезно знать, что сумма степеней любого одночлена, в данном случае, будет равна все той же старшей степени – 5.
Остается лишь корректно записать формулу, избавившись от нулевых степеней:
х5 – у5 = (х – у)(х4 + х3у + х2у2 + ху3 + у4)
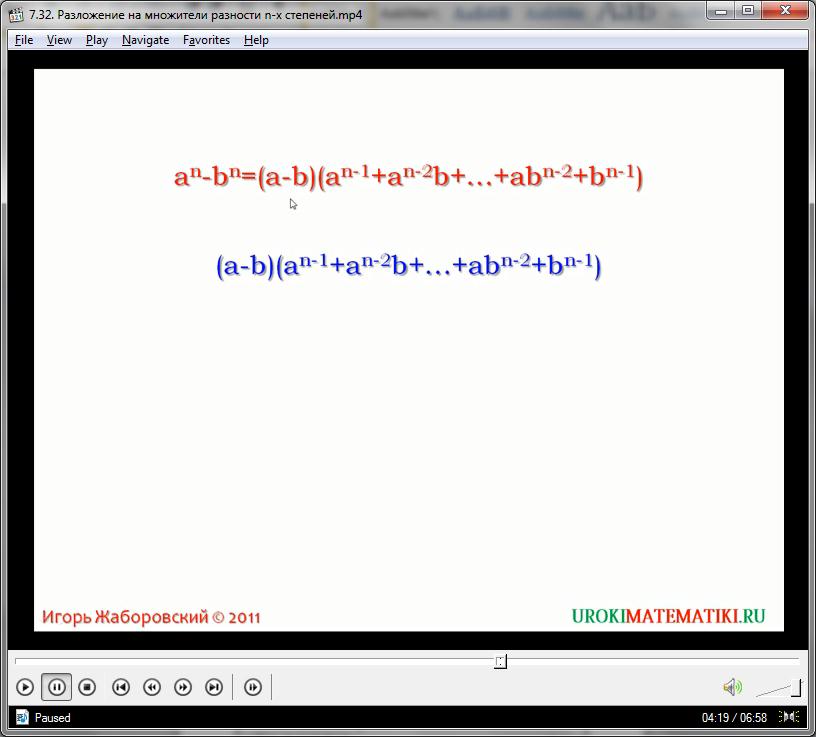
В общем плане, для любой степени n верно равенство:
(х)n – (у)n = (х – у)((х)n + (х)n-1у…+х(у)n – 1 + уn)
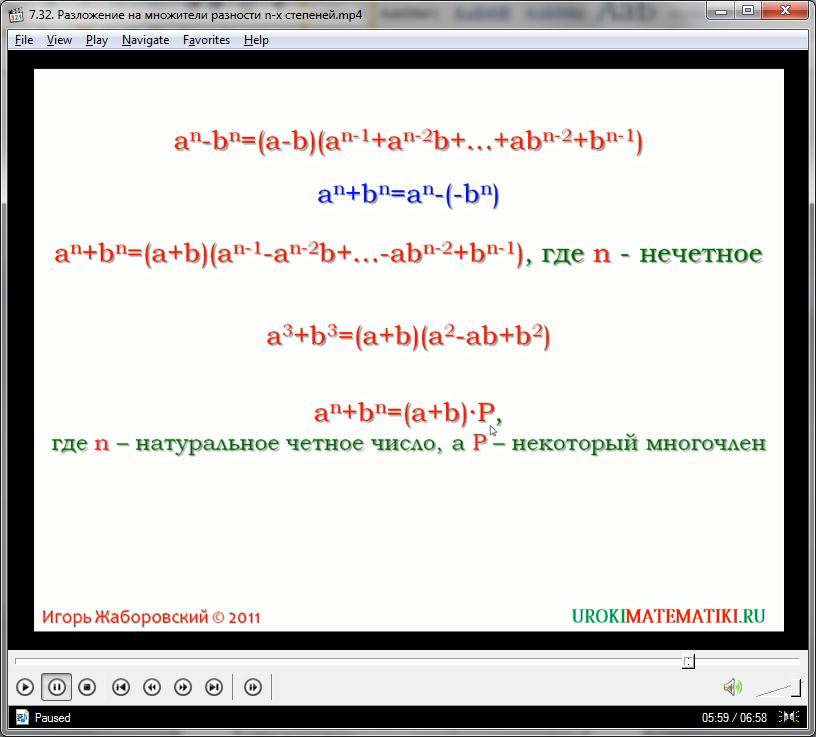
Универсальная формула для нахождения суммы двух выражений с n-ной разностью выводится через преобразование вида:
хn + уn = хn – (-уn)
Пользуясь формулой для разности выражений, полученной выше, выводим равенство:
хn + уn = хn – (-уn) = (х + у)((х)n-1 - (х)n-2у…- х(у)n – 2 + уn-1)
В силу того, что квадрат любого выражения ликвидирует его отрицательность, нельзя доступными средствами представить сумму квадратов (или любых четных степеней) переменных как произведение двух многочленов.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 25453 |
| Номер материала | 458 |