
Урок "Применение различных способов разложения многочленов на множители"

Краткое описание документа:
Многочлены являются важнейшим типом математических выражений. На основе многочленов построено множество уравнений, неравенств, функций. Задачи различного уровня сложности зачастую содержат этапы разностороннего преобразования многочленов. Так как математически любой полином представляет собой алгебраическую сумму нескольких одночленов, наиболее кардинальным и нужным изменением является преобразования ряда многочлена в произведение двух (или более) множителей. В уравнениях, обладающих возможностью обнуления одной из частей, перевод полинома на множители позволяет приравнять какую-то часть к нулю, и решить, таким образом, все уравнение.
Предыдущие видеоуроки показали нам, что в линейной алгебре существует три основных способа перевода многочленов в множители. Это вынесение общего множителя за скобки, перегруппировка по подобным членам, применение формул сокращенного умножения. Если все члены полинома обладают некой общей основой, то её легко можно вынести за скобки, оставив остатки от делений в виде измененного многочлена в скобках. Но чаще всего, один множитель не подходит под все одночлены, затрагивая лишь их часть. При этом, другая часть мономов может иметь свою общую основу. В таких случаях применяется способ группировки – по сути говоря, вынесение за скобки нескольких множителей, и создание комплексного выражения, которое можно преобразовать другими путями. И, наконец, существует целый комплекс специальных формул. Все они образованы абстрактными расчетами, использующими метод простейшего почленного переумножения. В ходе расчетов, многие элементы в начальном выражении сокращаются, оставляя небольшие многочлены. Что бы каждый раз не проводить емкие вычисления, можно применять готовые формулы, их обратные варианты, или обобщенные выводы этих формул.
На практике, часто бывает так, что в одном упражнении приходится комбинировать несколько приемов, в том числе, и из разряда преобразования многочленов. Рассмотрим пример. Разложить на множители бином:
3х3 – 3ху2
Выносим общий множитель 3х за скобки:
3х3 – 3ху2 = 3х(х2 – у2)
Как можно заметить на видео, вторые скобки содержат разность квадратов. Применяем обратную формулу сокращенного умножения, получая:
3х(х2 – у2) = 3х(х + у)(х – у)
Другой пример. Преобразуем выражение вида:
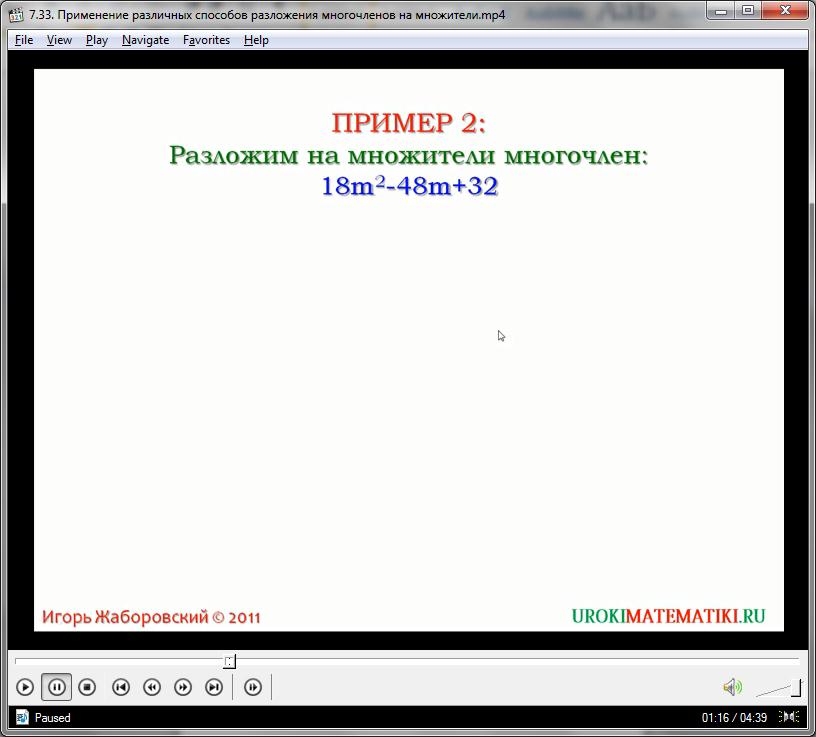
18а2 – 48а + 32
Уменьшаем числовые коэффициенты, вынося за скобки двойку:
18а2 – 48а + 32 = 2(9а2 – 24а + 16)
Что бы найти подходящую формулу сокращенного умножения для данного случая, необходимо несколько скорректировать выражение, подогнав под условия формулы:
2(9а2 – 24а + 16) = 2((3а)2 – 2(3а)4 + (4)2)
Порой, формулу в запутанном выражении увидеть не так просто. Приходится применять методы разложения выражения на составляющие элементы, или добавлять мнимые пары конструкций, типа +х-х. Корректируя выражение, мы должны соблюдать правила преемственности знаков, и сохранности значения выражения. При этом, нужно стараться привести многочлен к полному соответствию с абстрактным вариантом формулы. По нашему примеру применяем формулу квадрата разности:
2((3а)2 – 2(3а)4 + (4)2) = 2(3а – 4)
Решим более сложное упражнение. Разложим на множители многочлен:
у3 – 3у2 + 6у – 8
Для начала, проведем удобную группировку – первый и четвертый элемент в одну группу, второй и третий – во вторую:
у3 – 3у2 + 6у – 8 = (у3 – 8) – (3у2 – 6у)
Обратим внимание, что знаки во вторых скобках сменились на противоположные, так как мы вынесли минус за пределы выражения. В первых скобках можем записать так:
(у3 – (2)3) – (3у2 – 6у)
Это позволяет применить формулу сокращенного умножения для нахождения разности кубов:
(у3 – (2)3) – (3у2 – 6у) = (у – 2)(у2 + 2у + 4) – (3у2 – 6у)
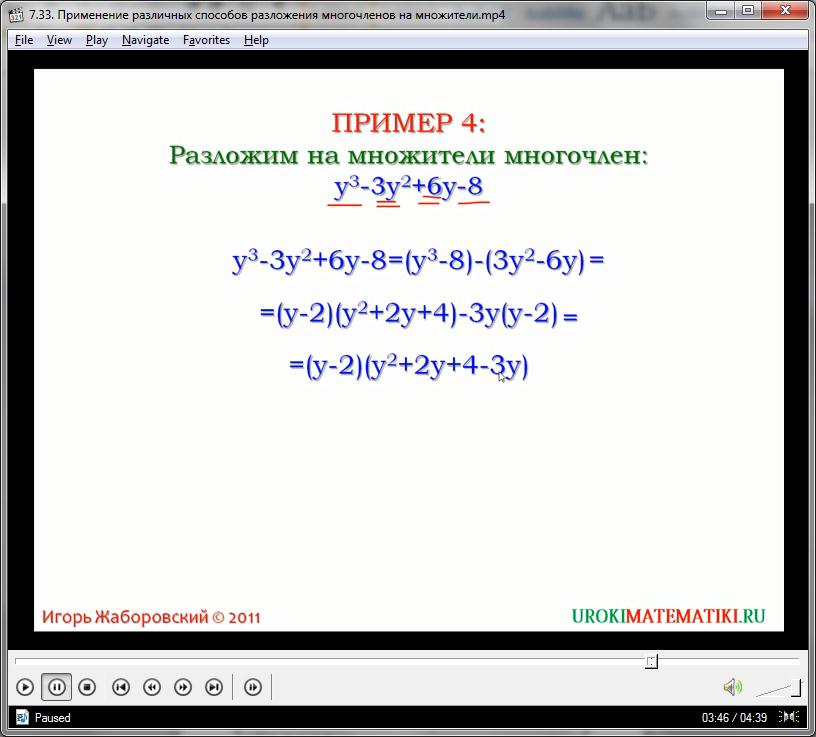
Выносим со вторых скобок общий множитель 3у, после чего, выносим из всего выражения (бинома) скобки (у – 2), приводим подобные слагаемые:
(у – 2)(у2 + 2у + 4) – (3у2 – 6у) = (у – 2)(у2 + 2у + 4) – 3у(у – 2) =
= (у – 2)(у2 + 2у + 4 – 3у) = (у – 2)(у2 – у + 4)
В общем приближении, существует определенный алгоритм действий при решении подобных упражнений.
1. Ищем общие множители для всего выражения;
2. Группируем подобные одночлены, ищем общие множители для них;
3. Стараемся вынести за скобки наиболее подходящее выражение;
4. Применяем формулы сокращенного умножения;
5. Если на каком-то этапе процесс не идет – вписываем мнимую пару выражений вида –х+х, или иные самоаннулирующиеся конструкции;
6. Приводим подобные слагаемые, сокращаем лишние элементы
Все пункты алгоритма редко когда применимы в одном задании, но общий ход решения любого упражнения по теме можно соблюдать в заданном порядке.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9803 |
| Номер материала | 460 |