
Урок "Разложение на множители суммы и разности кубов"

Краткое описание документа:
В серии видеоуроков, посвященных формулам сокращенного умножения, мы показали, что на практике очень часто применяется целая система взаимосвязанных равенств, помогающих значительно сократить процесс преобразования многочленов. В частности, были представлены формулы кубов разности и суммы двух натуральных выражений, имеющие абстрактный вид:
(а + х)3 = а3 + 3а2х + 3ах2 + х3
(а – х)3 = а3 – 3а2х + 3ах2 – х3
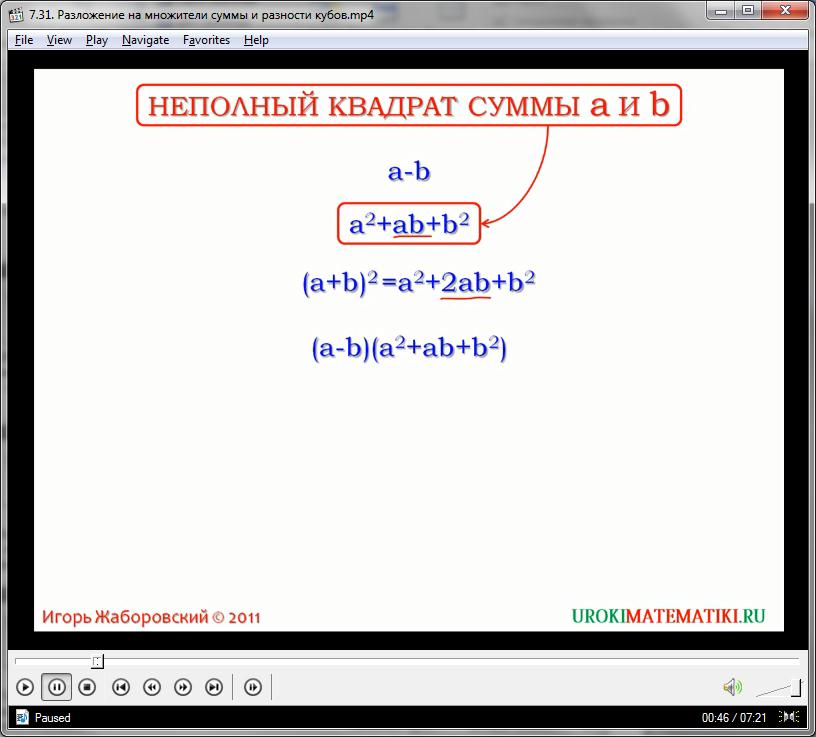
Продолжая изучать особенности работы с переменными третьей степени, вводим понятие разности кубов. Для этого представим себе следующее выражение:
а2 + ах + х2
В целом, данный пример очень похож на формулу квадрата суммы, только не хватает коэффициента, равного двум, у второго элемента. По сути, у нас есть сумма квадратов первого, второго выражений и их произведения. Такая конструкция в линейной алгебре именуется неполным квадратом суммы двух натуральных выражений.
Умножим неполный квадрат двух произвольных переменных на их разность:
(а – х)(а2 + ах + х2)
Используя прямое перемножение, получаем выражение вида:
(а – х)(а2 + ах + х2) = а3 + а2х + ах2 – а2х – ах2 – х3
Приводим подобные слагаемые, и сокращаем сложением данный многочлен:
а3 + а2х + ах2 – а2х – ах2 – х3 = а3 – х3
Иначе говоря:
(а – х)(а2 + ах + х2) = а3 – х3
Таким образом, мы получили новую формулу для определения разности кубов. Иначе говоря, произведение разности двух выражений на неполный квадрат суммы этих выражений равен разности кубов обеих выражений. Эта формула может успешно использоваться в двух направлениях. Можно приводить многочлены, по возможности, к виду разности кубов, и преобразовывать при помощи формулы в произведение двух множителей. Либо же быстро сократить сложное выражение, состоящие из подобной конструкции, до одного бинома с разностью.
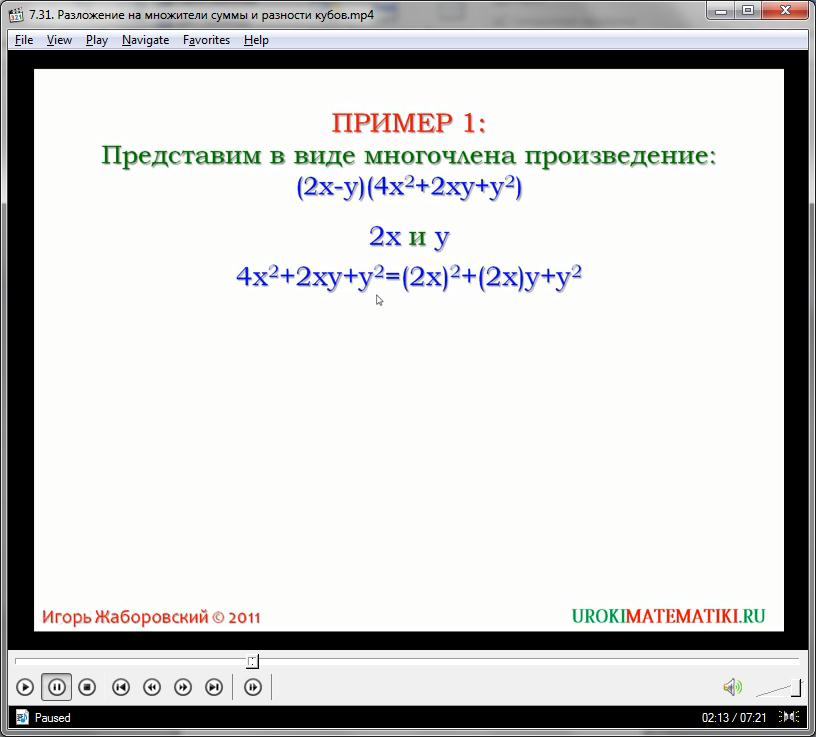
Рассмотрим представляемую формулу на примере. Необходимо преобразовать данное произведение в многочлен:
(2х – у)(4х2 + 2ху + у2)
Легко заметить, что во вторых скобках содержится двойное произведение переменных, что не соответствует определению неполного квадрата. Казалось бы, формула разности кубов тут не применима. Однако это выражение можно подогнать под условия формулы следующим образом:
2ху = (2х)у
4х2 = (2х)2
Введя данные выражения, можно с легкостью записать:
(2х – у)(4х2 + 2ху + у2) = (2х – у)((2х)2 + (2х)у + у2)
Теперь выражение полностью соответствует левой части вышеуказанной формулы для разности кубов, поэтому можно преобразовать так:
(2х – у)((2х)2 + (2х)у + у2) = (2х)3 – у3 = 8х3 – у3
Иногда квадратичное выражение представляет собой частичную форму многочлена, определяющего квадрат разности:
х2 – ху + у2
Выражение разности квадратов, не содержащее коэффициент, равный двум, при произведении одночленов, называется неполным квадратом разности.
Произведение суммы двух натуральных выражений на неполный квадрат разности всегда равно сумме кубов этих выражений. Докажем:
(х + у)(х2 – ху + у2) = х3 + х2у + ху2 – х2у – ху2 – у3
Сокращая подобные слагаемые:
х3 + х2у + ху2 – х2у – ху2 – у3 = х3 + у3
Иными словами, итоговая формула суммы кубов имеет такой вид:
(х + у)(х2 – ху + у2) = х3 + у3
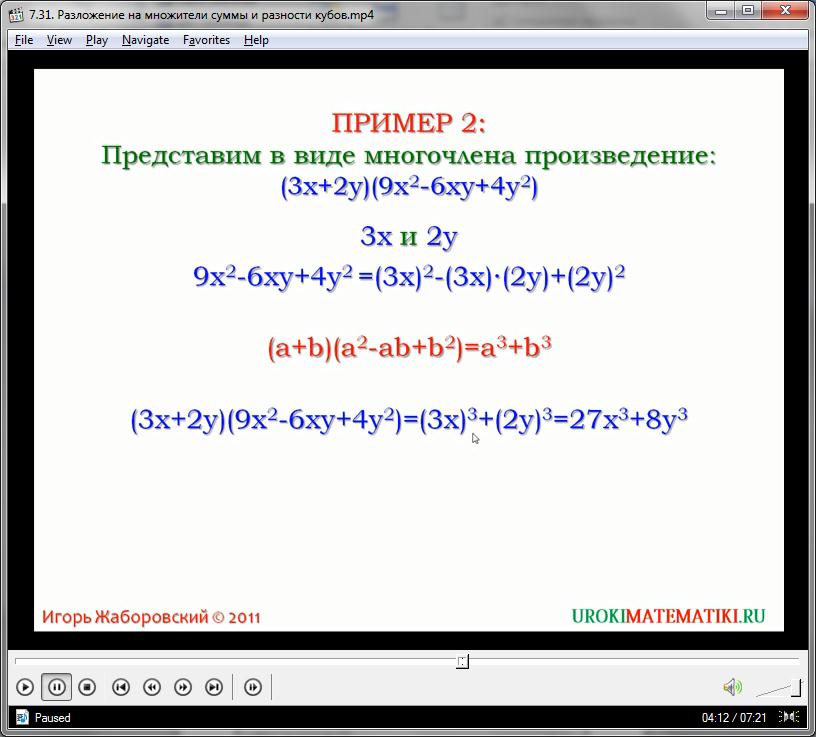
Проверим формулу на практике. Преобразуем в произведение такой многочлен:
1000х3 + 27у3
При этом главное не забывать, что коэффициенты перед переменными имеют свою прямую связь со степенью. Когда числовое значение при неизвестной не равно единице, следует извлекать из него кубический корень (если это возможно), приписывать полученное значение к самой переменной и ставить весь одночлен в скобки, вынося третью степень за их пределы:
1000х3 + 27у3 = (10х)3 + (3у)3
Такой подход позволяет не только корректно воспользоваться формулой, но и избежать возможных ошибок. Преобразуем выражение по равенству для суммы кубов:
(10х)3 + (3у)3 = (10х + 3у)((10х)2 – 10х3у + (3у)2) =
= (10х + 3у)(100х2 – 30ху + 9у2)
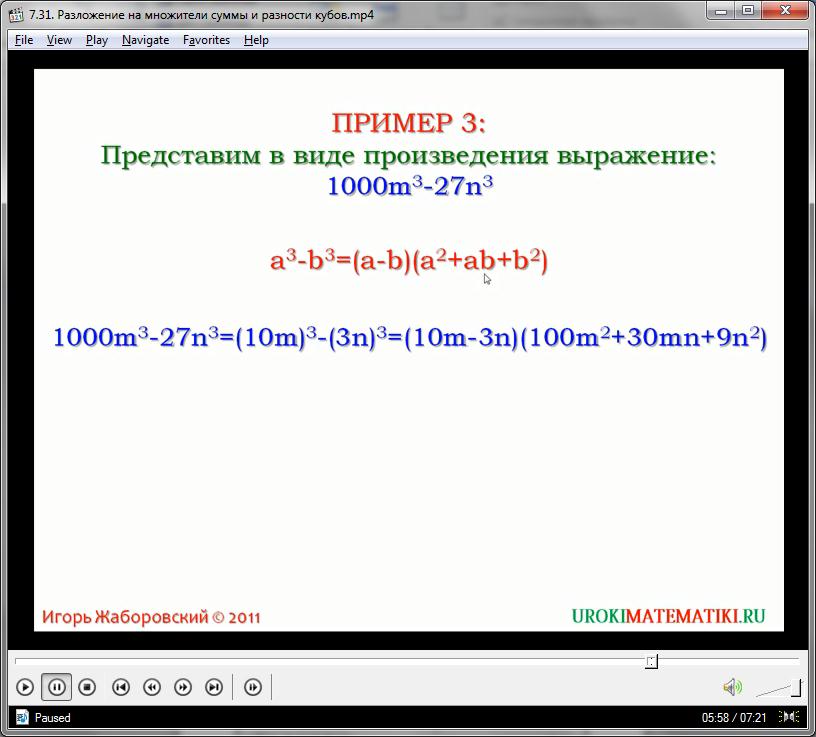
И переменная, и коэфициент при ней равномерно возводятся в квадратичную степень – поэтому лучше писать одночлен в скобках до самого раскрытия.
Видео советует ещё одно прекрасное упражнение. Преобразуем:
8х3 + 0,001у3
Выделяем основные одночлены, внося коэффициенты внутрь скобок:
8х3 + 0,001у3 = (2х)3 + (0,1у)3
Применяем формулу суммы кубов:
(2х)3 + (0,1у)3 = (2х + 0,1у)((2х)2 – 2х0,1у + (0,1у)2 =
= (2х + 0,1у)(4х2 – 0,2ху + 0,01у2)
Преобразование биномов, построенных на разности кубов, бывает весьма полезным в решении различных кубических уравнений. Создание произведения двух множителей приводит к возможности уравнять содержимое каких-либо скобок к нулю, преобразовав уравнение в обычное квадратичное равенство.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7726 |
| Номер материала | 459 |