
Урок "Возведение в куб суммы и разности"

Краткое описание документа:
В серии видеоуроков о формулах сокращенного умножения представлены наиболее часто используемые равенства, которые помогают с легкостью преобразовывать даже некоторые довольно сложные по структуре многочлены. В предоставляемом видео мы подробно изучим формулу куба суммы и разности двух чисел.
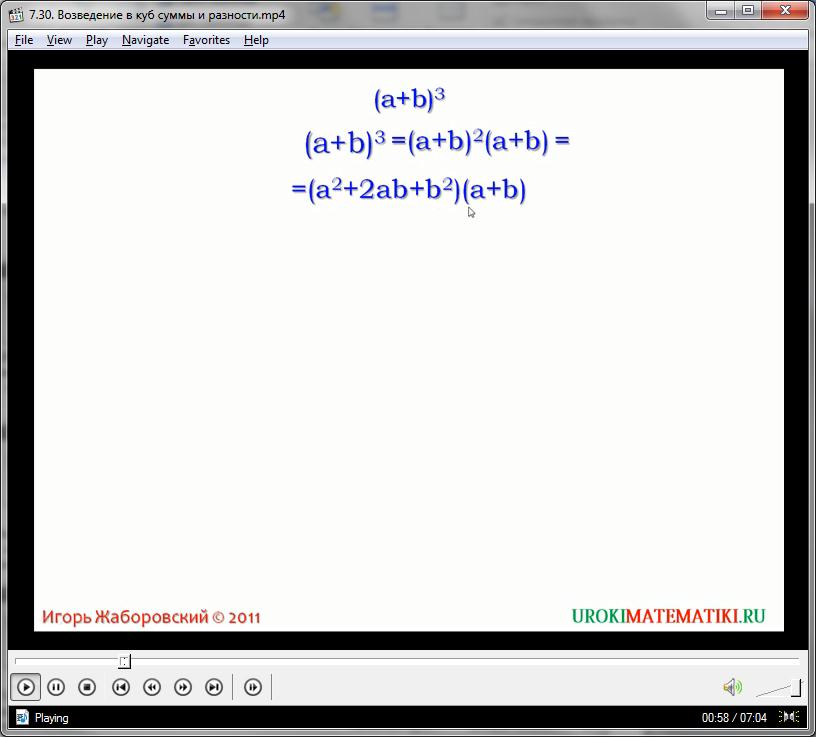
Предположим, нам задано найти куб суммы двух переменных:
(х + у)3
Чтобы определить это выражение, можно записать его прямым образом и перекрестно перемножить каждый элемент. Но в случае куба это несколько затруднительно осуществить – двойное перемножение порождает ошибки вычисления. Чтобы их избежать, перепишем исходное выражение следующим образом:
(х + у)3 = (х + у)(х + у)(х + у) = (х + у)2(х + у)
Теперь, воспользовавшись формулой сокращенного умножения для квадрата суммы, мы можем записать:
(х + у)2(х + у) = (х2 + 2ху + у2)(х + у)
Тут можно применить правило умножения двух многочленов и раскрыть скобки:
(х2 + 2ху + у2)(х + у) = х3 + х2у + 2х2у + 2ху2 + ху2 + у3 =
= х3 + 3х2у + 3ху2 + у3
Финальное выражение является формулой, определяющей куб суммы любых двух выражений. Словесно можно заключить: куб суммы двух натуральных выражений равен сумме куба первого выражения, куба второго выражения, утроенного произведения квадрата первого выражения на второе и утроенного произведения первого выражения на квадрат второго.
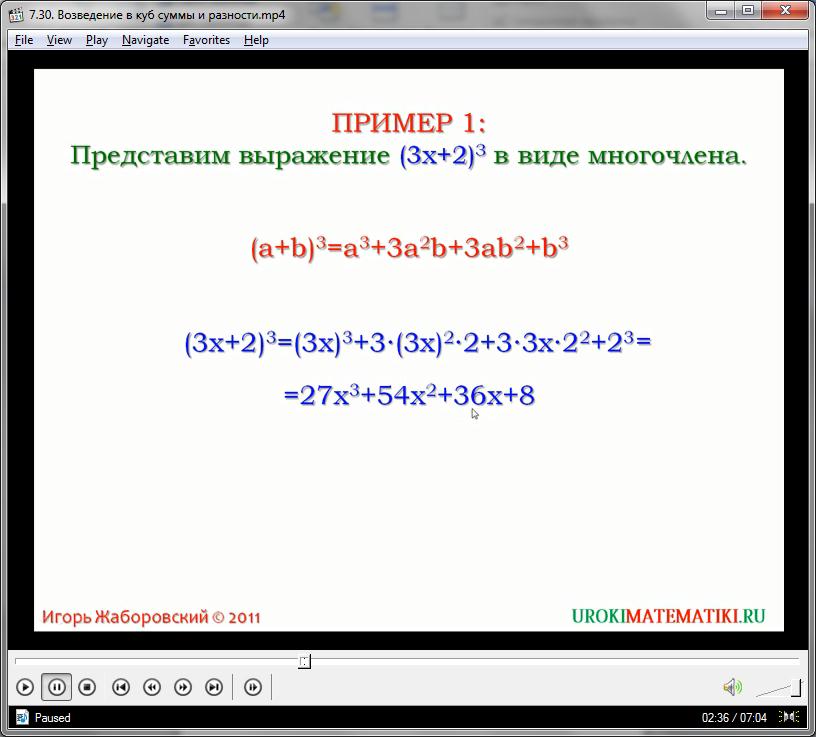
Для усвоения формулы, рассмотрим несколько примеров.
Решить выражение:
(х + 3)3
Используя формулу, выведенную нами в этом видеоуроке, записываем, раскрывая скобки:
(х + 3)3 = х3 + 3(х2(3)) + 3(х(3)2) + (3)3 =
= х3 + 9х2 + 27х + 27
Возвести в куб бином вида:
(-3х + 5)
Перед первым одночленом стоит знак минус – это не мешает применять формулу (так как она подходит под любую алгебраическую сумму), однако стоит учитывать знаки и их преемственность. Можно сразу записать таким образом:
(-3х + 5) = ((-3х) + 5)
Применяя формулу для куба суммы, получаем:
((-3х) + 5)3 = (-3х)3 + 3((-3х)2(5) + 3((-3х)(5)2) + (5)3 =
= -27х3 + 135х2 – 225х + 125
Теперь рассмотрим куб разности двух выражений. Необходимо вставить ремарку, что в данном контексте понятия «сумма» и «разность» весьма относительны. Фактически, мы имеем один многочлен, состоящий из некоторого числа элементов (в этом случае – из двух), обладающих числовыми коэффициентами, отличными от нуля. При этом коэффициенты могут быть как положительными, так и отрицательными – принципиально многочлен и формулы, применяемые к нему, остаются прежними. Все одночлены полинома связаны алгебраическим суммированием вне зависимости от знаков при коэффициентах. Поэтому формулу куба суммы успешно можно использовать и для нахождения куба разности, обособив минусы в скобках. По сути, нижепредставленное равенство, является всего лишь частным следствием формулы для куба суммы.
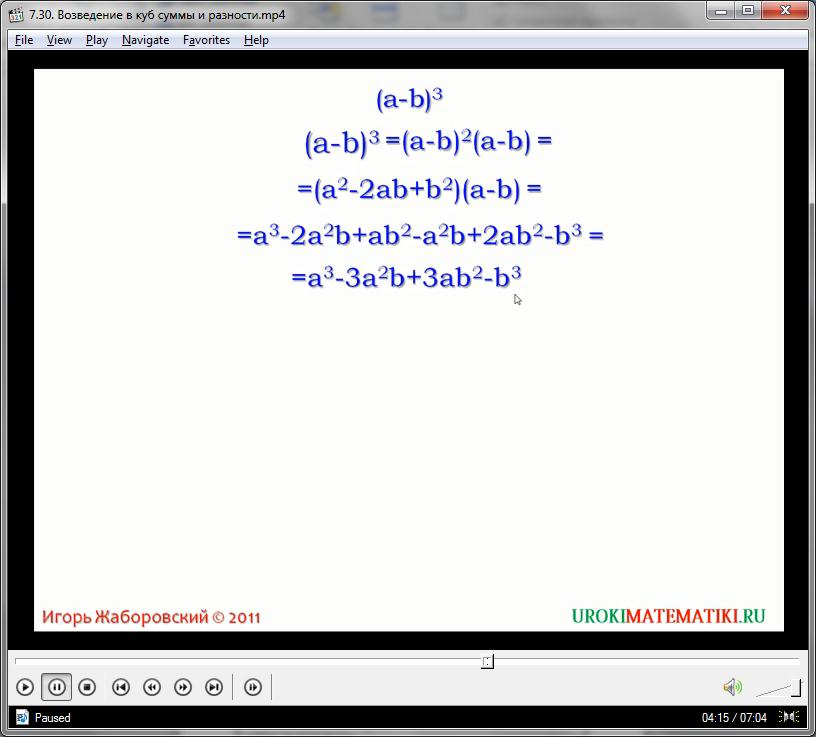
Используя абстрактный пример и формулы сокращенного умножения более низкого порядка, рассчитаем:
(х – у)3 = (х – у)(х – у)(х – у) =
= (х – у)2(х – у) = (х2 – 2ху + у2)(х – у) =
= х3 – 3х2у + 3ху2 – у2
Полученное выражение можно использовать в качестве формулы для нахождения куба разности. Иначе говоря: куб разности двух натуральных выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, минус куб третьего выражения. Определяя данное равенство, следует помнить о сложной преемственности знака «минус» в полистепенных выражениях.
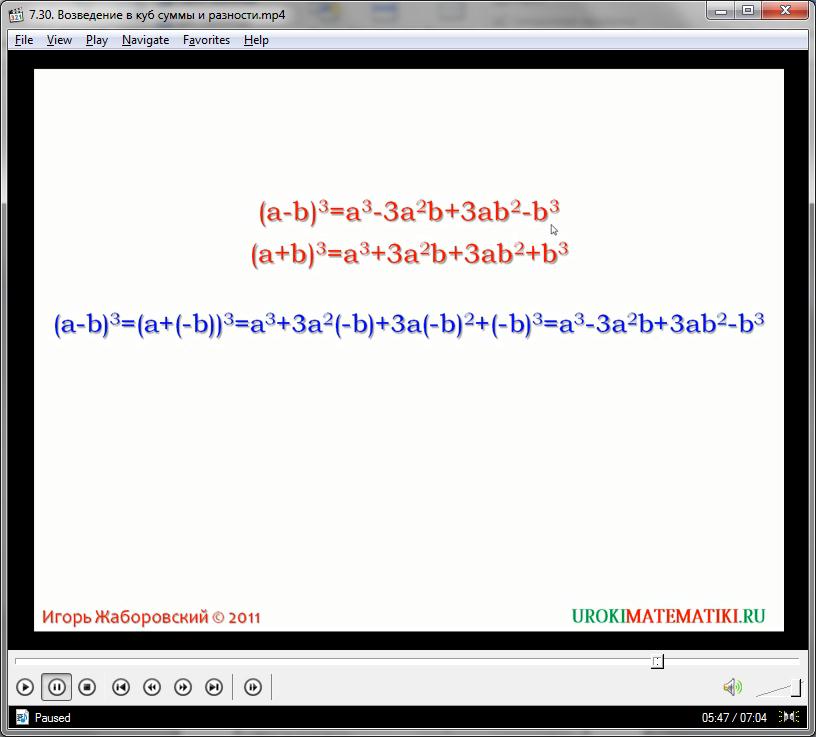
Если сравнить между собой формулы для нахождения куба разности и суммы одной и той же пары выражений, можно найти только два отличия. В равенстве для нахождения равенства появляется минус у утроенного произведения квадрата первого выражения на второе (потому что второе несет минус, ничем не аннулируемый), а также минус у куба второго выражения (потому что третья степень сохраняет знак неизменным).
Для примера, решим упражнение:
(2х – 2)3
Применяя формулу куба разности, получаем:
(2х – 2)3 = (2х)3 – 3(4х2(2)) + 3(2х(4)) – (2)3 =
= 8х3 – 24х2 + 24х – 8
Применение формул для нахождения куба разности и суммы помогает в упрощении многих сложных многочленов, а также в решении квадратичных и кубических уравнений.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9973 |
| Номер материала | 457 |