
Урок "Длина окружности"

Краткое описание документа:
Видеоурок «Длина окружности» дает подробное углубленное понятие о том, что такое длина окружности и вывод математического аппарата для ее вычисления. Задача данного видеоматериала – сформировать у учеников представление о длине окружности, объяснить, как образуется формула для нахождения длины окружности. Видеоурок может повысить эффективность традиционного урока математики за счет освобождения учителя от необходимости расходовать время на подачу стандартного блока учебного материала. Освобожденное время учитель может использовать на усиление индивидуальной работы.
Данный видеоматериал может использоваться как наглядное пособие для сопровождения объяснения учителя или как самостоятельная часть урока вместо объяснения учителя. Наглядность учебного материала достигается с помощью анимационных эффектов. Иллюстрации с помощь анимации преобразуются, меняют форму, дорисовываются детали. Благодаря возможности выделения цветом, подчеркивается важность деталей построения, формулы и формулировки.
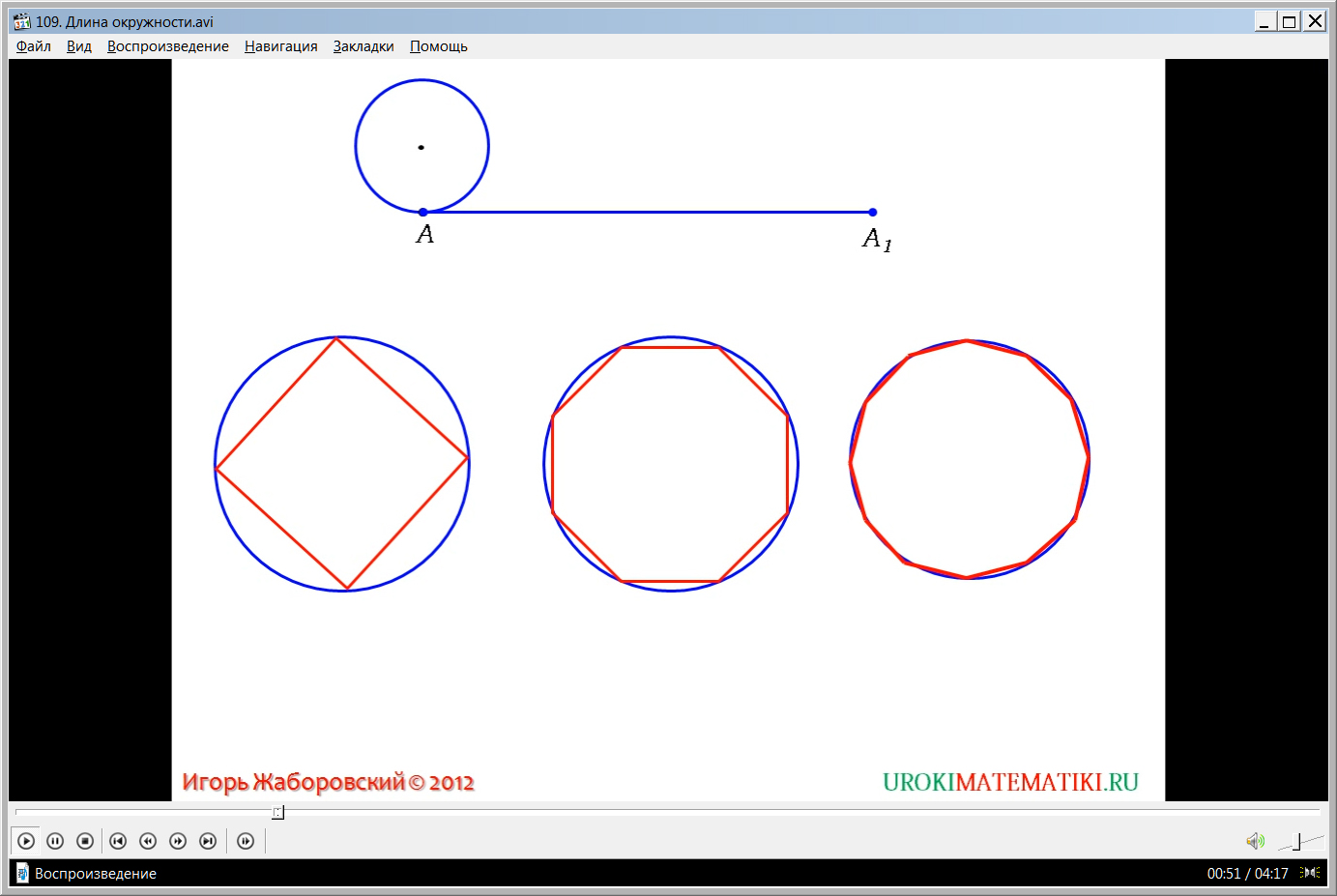
Видеоурок начинается с представления темы. Чтобы сформировать у учеников представление о длине окружности, на рисунке рисуется окружность, которую рекомендуется представить изготовленной из тонкой нити, которая не растягивается. После разрезания данной нити и вытягивания ее в длину, образуется отрезок АА1. Если измерить длину полученного отрезка, они и будет являться длиной окружности. Отмечается, что если в некоторую окружность
вписывается многоугольник, то значение его периметра приближенно равно длине описанной окружности. Чем больше сторон имеет многоугольник, который вписан, тем ближе значение периметра к величине длины окружности. На экране демонстрируется квадрат, вписанный в окружность, рядом – вписанный восьмиугольник, 12-угольник, вписанный в такую же окружность. На рисунке видно, что чем больше количество сторон многоугольника, тем ближе они прилегают к самой окружности, повторяя ее. Отмечается, что длина окружности - предел, к которому стремится при увеличении количества сторон периметр вписанного многоугольника.
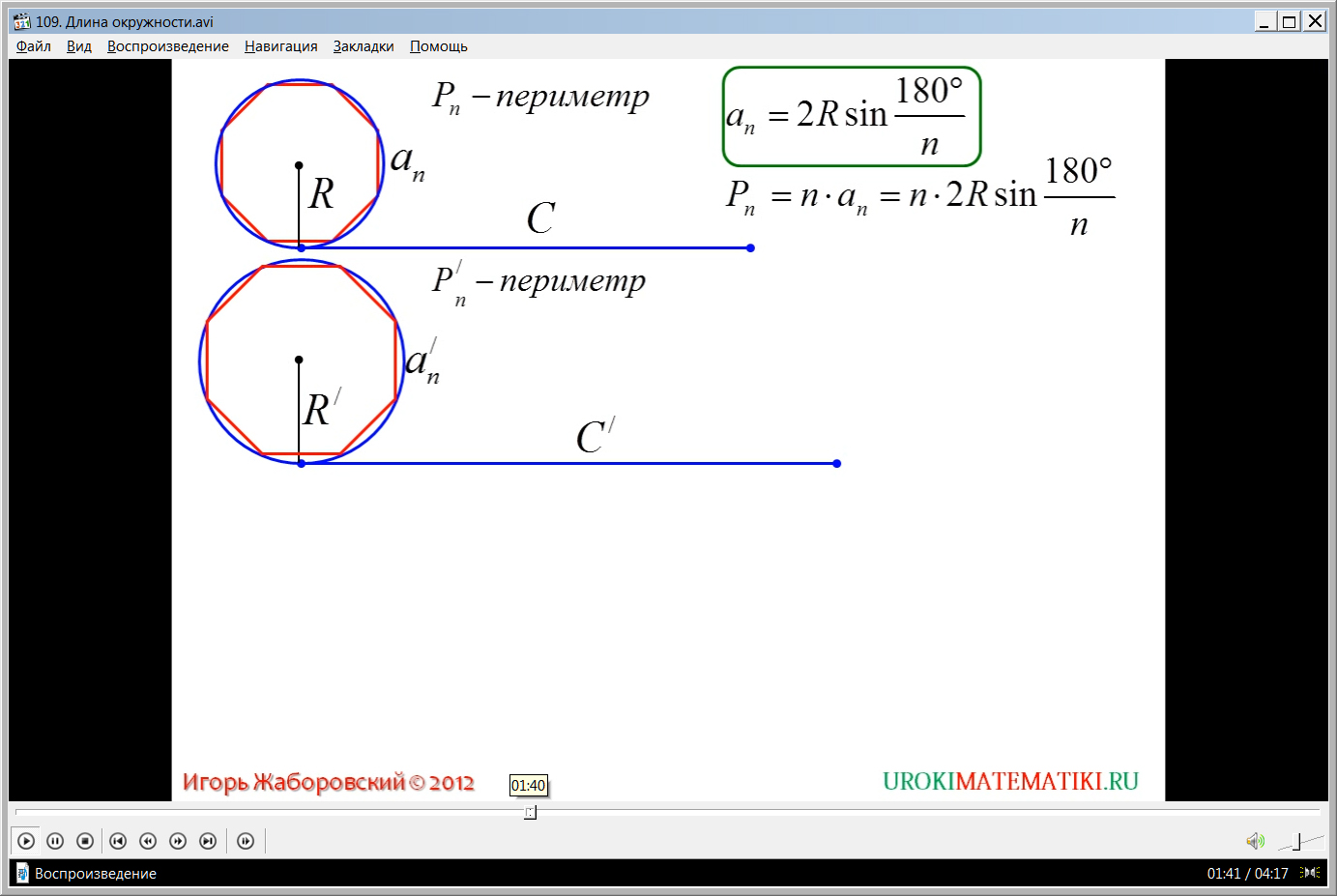
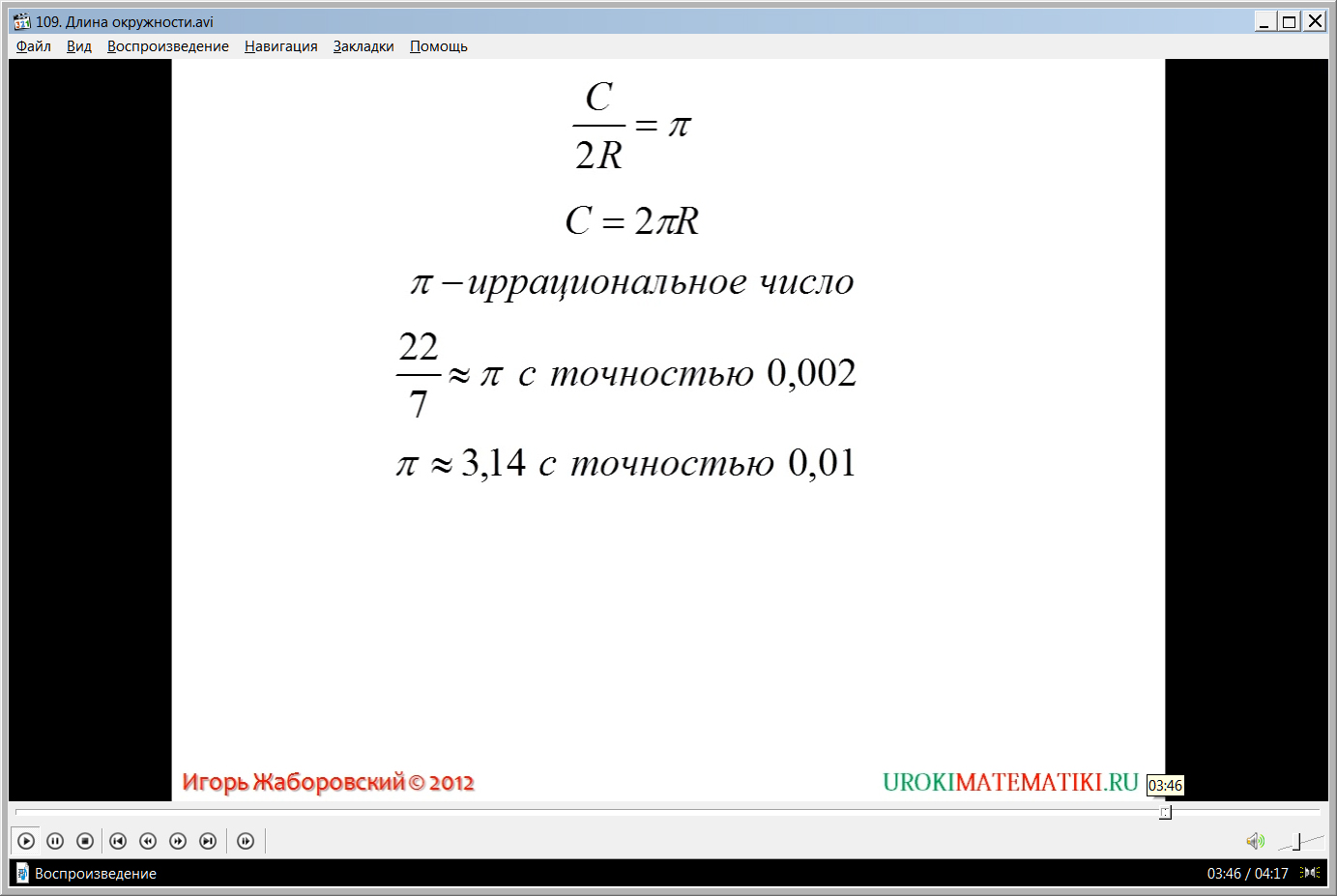
Далее предлагается рассмотреть выведение формулы длины окружности через ее радиус. Для этого на экране строятся две окружности радиусами Rи R’. Их длины составляют С и С’. В каждую окружность вписывается правильный n-угольник. Для каждого n-угольника вводятся обозначения сторон – anи an’, периметров – Pnи Pn’. Для определения периметра многоугольника используется известная формула для вычисления стороны многоугольника an. =2Rsin180°/n. При подстановке ее в формулу для нахождения периметра получаем Pn= n·an= n·2Rsin180°/n, а для нахождения периметра многоугольника, вписанного во вторую окружность, получается Pn’= n·an’= n·2R’sin180°/n. Если анализировать отношение периметров построенных многоугольников, то при приближении количества углов многоугольника к бесконечному числу очевидно, что и периметр их будет приближаться к длине описанной окружности, а Pn/Pn’ приближается к Сn/Сn’. Так как отношение длин окружности пропорционально отношению радиусов Сn/Сn’=2R/2R’, то справедливо отношение Pn/Pn’=2R/2R’. Отсюда следует, что Сn/2R = Сn’/2R’. Подчеркивается вывод, сделанный из анализа – для всех окружностей отношение длины к диаметру является одним и тем же числом. Таким образом определяется число π. Из рассматриваемого отношения получаем вывод, что Сn/2R =π. Отсюда формула для определения длины окружности Сn=2πR.

Отмечается, что выведенное при помощи сделанного анализа число π является иррациональным числом. Оно может быть определено с точностью до 0,002 из дроби 22/7. Ученики осведомляются, что данное число было выведено еще в древности – его в III веке до н.э. получил греческий математик Архимед. Для решения задач используется значение числа π с точностью до 0,01, то есть π≈3,14.
Далее рассматривается выведение формулы для дуг окружности l, которая образована углом с градусной мерой α. Для начала определяется длина дуги угла в 1°. Зная длину окружности Сn=2πR и градусную меру окружности 360°, можно определить длину дуги одного градуса 2πR/360°=πR/180°. Чтобы вычислить длину дуги окружности некоторого угла α используется формула l= πRα /180°.
Видеоурок «Длина окружности» рекомендуется применять для повышения эффективности традиционного урока математики в школе. Также данный материал может послужить инструментом для формирования необходимых понятий в ходе дистанционного обучения. Подробное понятное объяснение в видео также рекомендуется ученикам, которые самостоятельно осваивают предмет или требуют дополнительных занятий для формирования более глубокого понимания предмета.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 3821 |
| Номер материала | 750 |