
Урок «Дробные рациональные уравнения»

Краткое описание документа:
Видеоурок «Дробные рациональные уравнения» содержит информацию о дробных рациональных уравнениях, способах их решения, примеры решения таких заданий. С помощью данного пособия учитель может более эффективно решать задачи урока, формировать умение учеников решать дробные рациональные уравнения.
Использование материала в виде видеоурока дает возможность учителю уделить больше внимания индивидуальной работе с учениками, сконцентрировать их на работе с данным учебным материалом. Специальные приемы, используемые в видео – анимационные эффекты, выделение цветом, рамкой важных деталей и понятий улучшает запоминание материала, способствует его освоению.
Видеоурок начинается с представления темы урока. Затем на примерах х/(х2-1)=5/(х+1), а также √3/х2=х+5, и 2х-1=х/(х+12) демонстрируется понятие о дробном рациональном уравнении как уравнении, части которого представляют собой рациональные выражения, при этом одна или обе - дробные. Определение выделено в рамку для запоминания.
Далее на экране представляется ход решения дробных уравнений поэтапно:
- поиск общего знаменателя дробей;
- перемножение обеих частей на общий знаменатель;
- нахождение решений полученного целого уравнения;
- исключение из корней, обращающих общий знаменатель в 0.
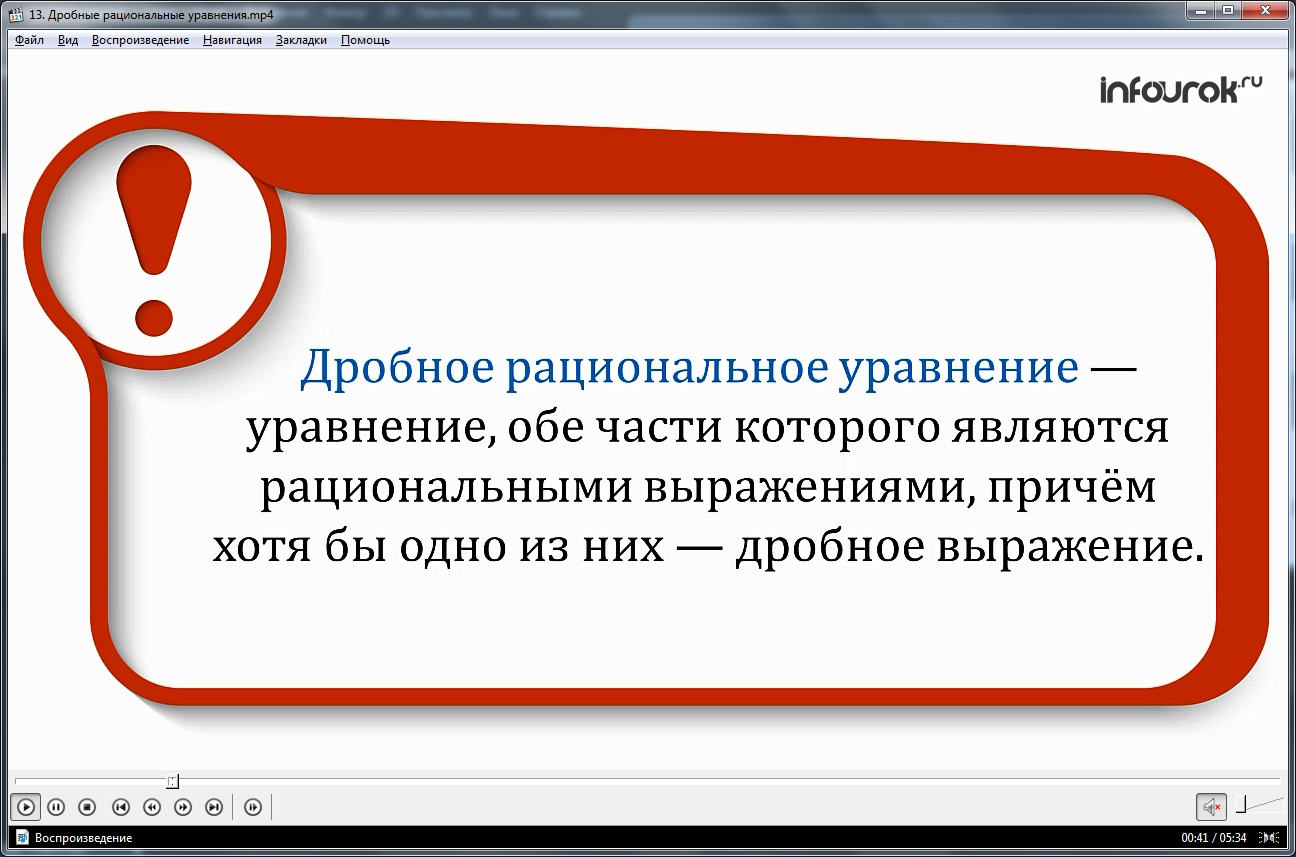
Рассматривается пример решения дробного уравнения 2/(х-2)-10/(х-3)=(50/(х2+х-6))-1. Согласно общему плану решения, сначала определяется общий знаменатель дроби. Он равен х2+х-6. После перемножения обеих частей данного уравнения на общий знаменатель, получается целое уравнение -8х+26=-х2-х+56. Все члены уравнения переносятся в левую часть, после чего образуется уравнение второго порядка х2-7х-30=0, для решения которого вычисляется дискриминант D=169 и корни уравнения х1=-3 и х2=10.Для исключения неверных корней, подставляем полученные значения в общий знаменатель. Так как при подстановке корня х=-3 общий знаменатель обращается в нуль, это значение не является решением уравнения. Единственным решением уравнения является 10.
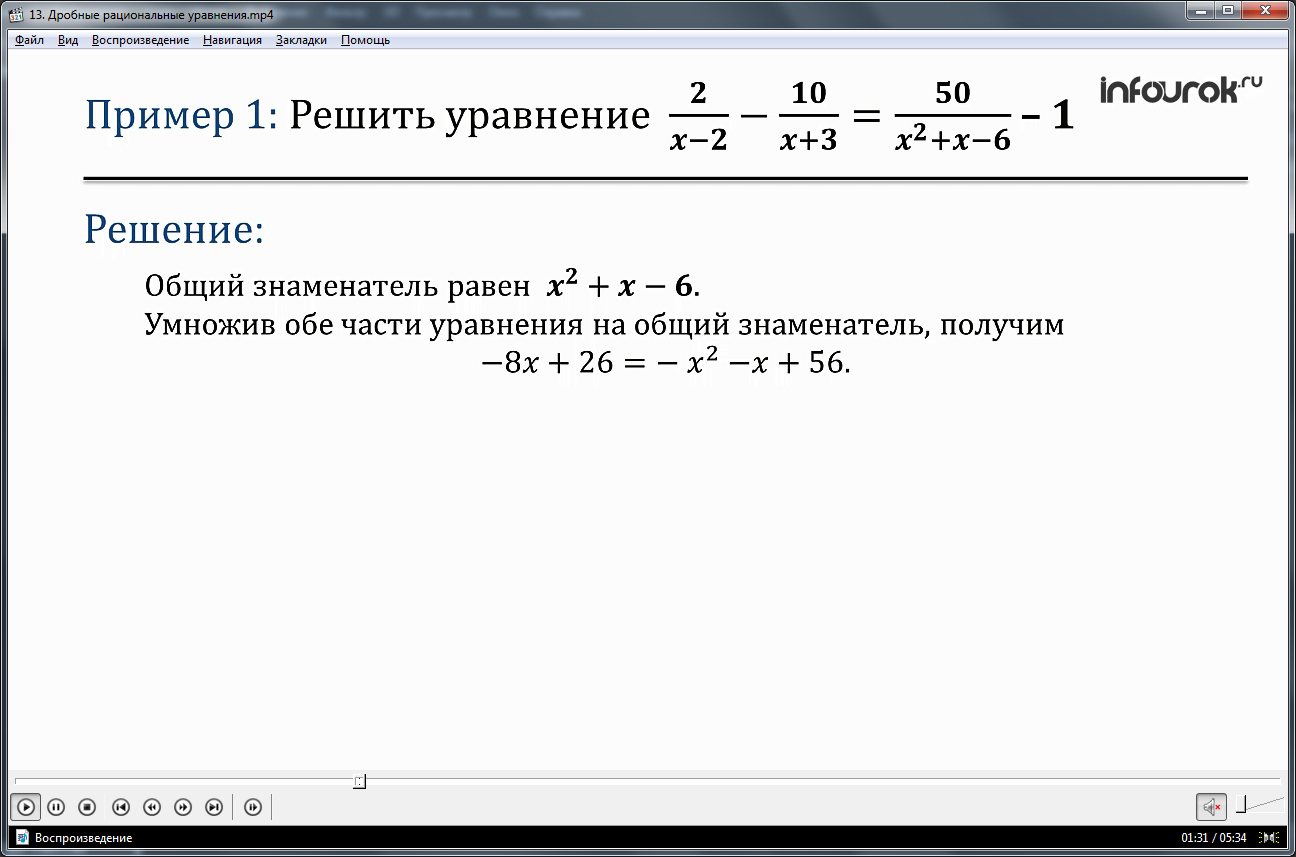
Следующий пример дает возможность наблюдать решение дробного рационального уравнения, в знаменателе которого есть только двучлены: 1/(х+3)-1/(х+9)=1/(х+5)-1/(х+21). Для решения уравнения приводятся к общему знаменателю обе части уравнения. После вычислений в числителе образуется уравнение с квадратным многочленом в числителе в обеих частях: 6/(х2+12х+27)=16/(х2+26х+105). После преобразования уравнения получается равенство произведений 6(х2+26х+105)=16(х2+12х+27). Раскрыв скобки и перенеся все члены уравнения в левую часть, получим квадратное уравнение 10х2+36х-198=0. Решением данного уравнения будут х1=-6,6 и х2=3. При подстановке полученных корней в выражение общего знаменателя, в результате вычислений не образуется нуль, поэтому оба они являются решениями исходного уравнения.
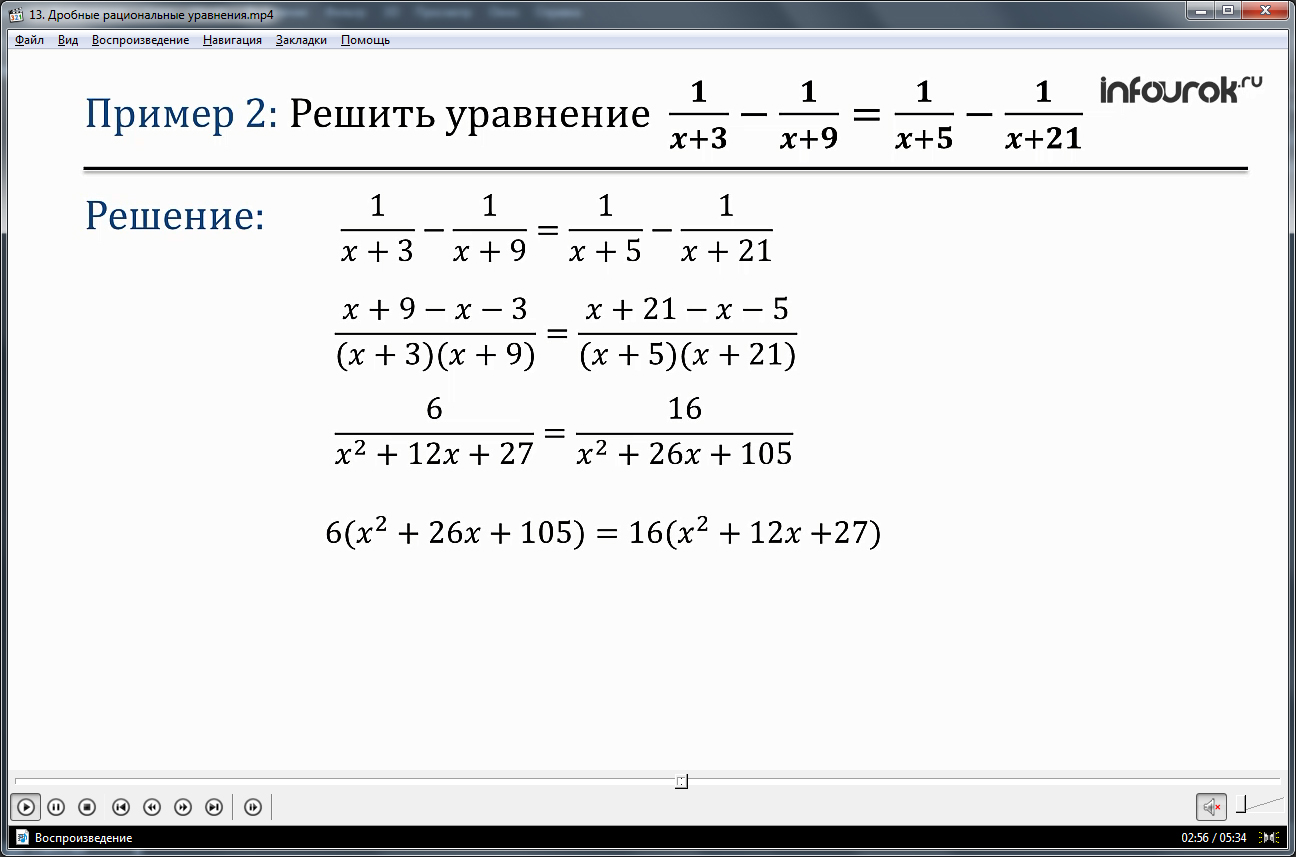
Пример 3 демонстрирует решение уравнения 3х/(х-2)+6/(2-х)=х. Очевидно, общим знаменателем данного дробного рационального уравнения будет х-2. Умножение обеих частей уравнения на общий знаменатель даст уравнение 3х-6=х(х-2), которое после преобразования к стандартному виду приминает вид уравнения второй степени х2-5х+6=0. Корнями данного уравнения являются х1=2 и х2=3. При подстановке первого корня в выражение общего знаменателя, он обращается в 0, поэтому х=2 не будет корнем исходного уравнения. Второе значение корня не обращает знаменатель в 0, поэтому является корнем уравнения.
При решении последнего примера 16/(х2-2х)-11/(х2-2х+3)=9/(х2-2х+1) важно определить сначала его особенность, которая подсказывает способ решения. Во всех выражениях есть (х2-2х), поэтому для упрощения решения задания следует ввести новую переменную у=х2-2х. Подставив новую переменную в выражения, умножив обе части на общий знаменатель и приведя уравнение к стандартному виду, получаем квадратное уравнение 2у2-13у-24=0. Уравнение имеет два корня у1=-1,5 и у2=8. При подстановке первого корня в выражение для определения переменной у корни отсутствуют. Подстановкой корня у=8 в выражение для переменной получаем два значения х1=4 и х2=-2. Таким образом, решениями данного уравнения будут корни х1=4 и х2=-2.
Видеоурок «Дробные рациональные уравнения» может быть использован на уроке алгебры при объяснении нового материала. Также подробное объяснение способов решения дробных уравнений поможет ученику освоить умение решать подобные задания самостоятельно. Также материал может быть полезен при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8753 |
| Номер материала | 660 |