
Урок "Формула для вычисления площади правильного многоугольника, его сторон и радиуса вписанной окружности"

Краткое описание документа:
Видеоурок «Формулы для определения площади правильного многоугольника, а также его сторон, вычисления радиуса вписанной окружности» демонстрирует выведение формул, которые необходимы для решения задач, в которых требуется определить элементы правильного многоугольника. Рассматривается, каким образом получаются формулы для определения площади правильного многоугольника, стороны, радиуса вписанной окружности. Это наглядное пособие помогает учителю подробно и понятно продемонстрировать учебный материал. Наглядное пособие может быть использовано для сопровождения объяснения учителя. Также оно может полностью заменить учителя при подаче новой темы, так как озвучено и дополнено важными комментариями. Видеоурок помогает более рационально распределить время урока, освободить учителя для индивидуальной работы, повысить эффективность обучения.
Материал в видеоуроке структурирован, последовательно подается в форме, удобной для обучения. При помощи анимационных эффектов представлены построения, производится структурирование подачи, дается понятное разъяснение в деталях. Важные формулировки и детали выделяются цветом для лучшего усвоения материала, более глубокого его понимания. Используя видеоурок, учителю легче сконцентрировать внимание учеников на изучении предмета, добиться целей обучения.
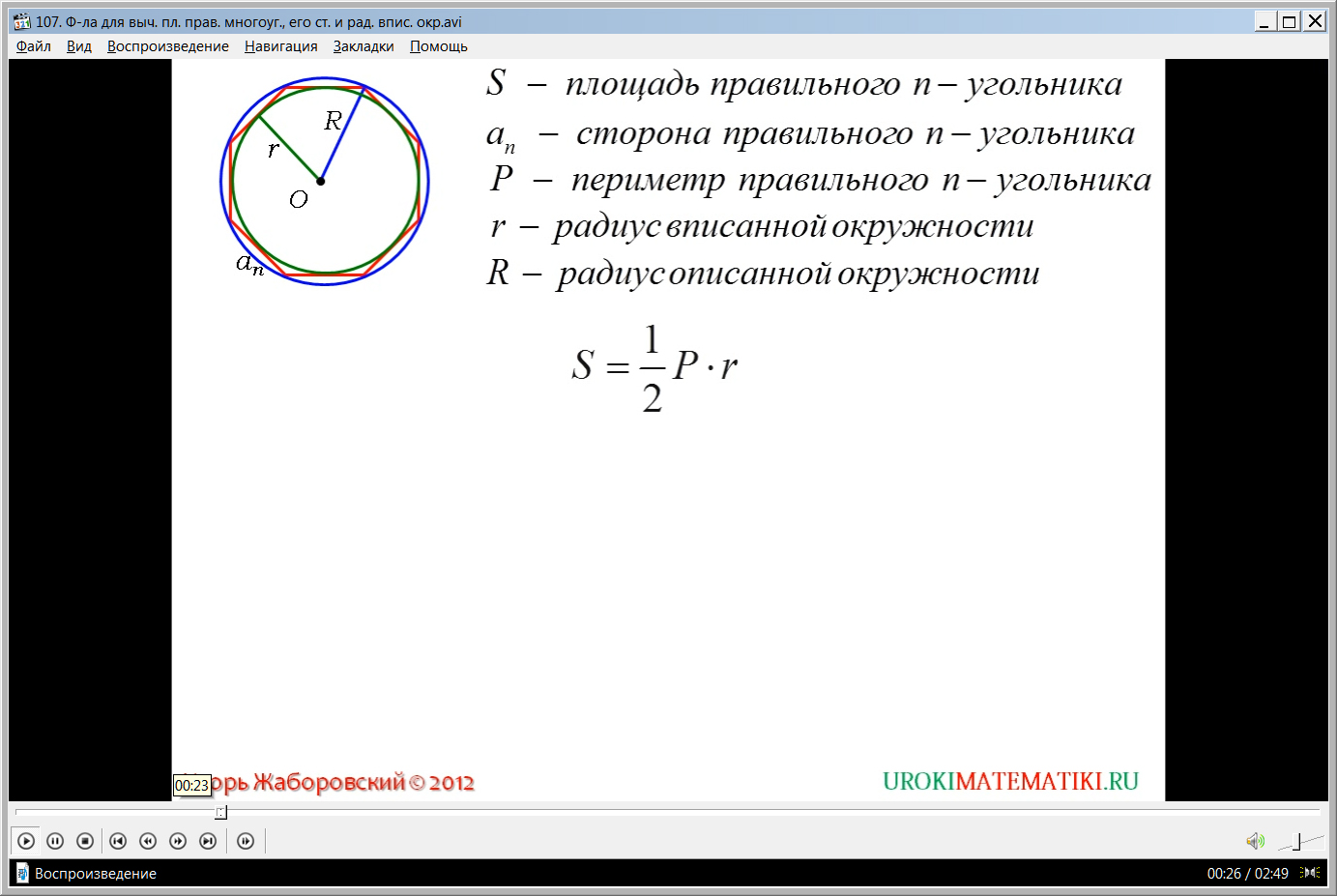
Видеоурок начинается с представления темы. Строится правильный многоугольник. Вокруг него описывается окружность, а также демонстрируется вписанная окружность. В построенном многоугольнике отмечаются центр многоугольника, сторона an, радиус вписанной окружности обозначается r, а для обозначения радиуса описанной окружности вводится R. Отмечается также, что площадь многоугольника обозначается S.
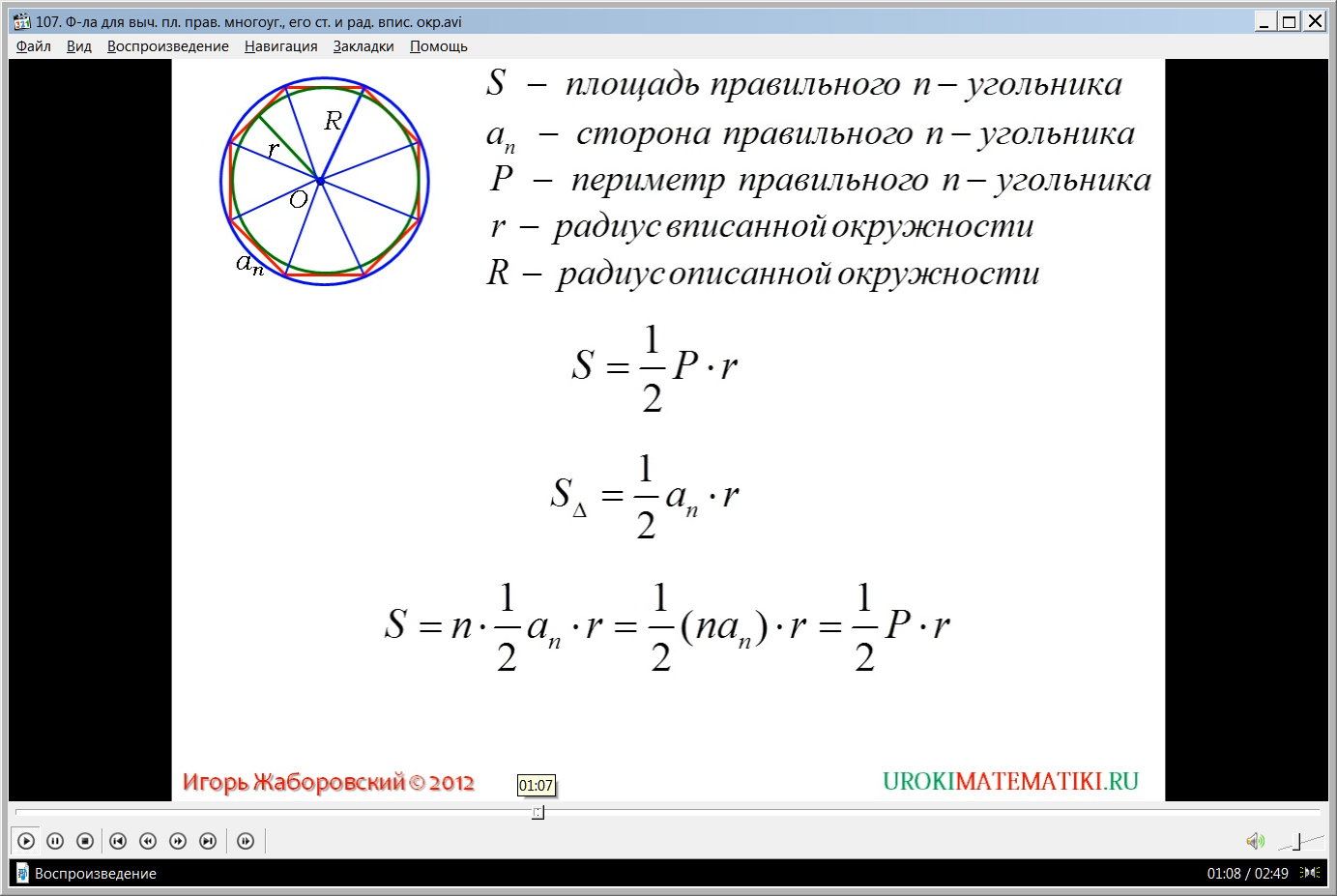
Предлагается рассмотреть вывод формулы для определения площади многоугольника. В конечном виде данная формула S=(1/2)P·r. На рисунке построенный n-угольник разбивается отрезками, выходящими из вершин многоугольника к центру, на n треугольников. Площадь каждого из образованных треугольников определяется формулой S=(1/2) an·r. Чтобы найти площадь всего многоугольника, умножаем площадь одного треугольника на их количество S=n·(1/2) an·r. При этом очевидно, что произведение n·an представляет собой периметр многоугольника. При его подстановке в формулу получаем ее конечный вид S=(1/2)P·r.
Чтобы вывести формулы, по которым можно вычислить сторону многоугольника, а также радиус вписанной окружности, на рисунке рассматривается треугольник, образованный перпендикуляром, проведенным к стороне многоугольника, половиной стороны и отрезком, соединяющим центр многоугольника, а также его вершину. Полученный треугольник А1Н1О является прямоугольным. Рассматривая треугольник А1Н1О, можно заметить, что угол А1 является половиной угла многоугольника, то есть А1=αn/2=((n-2)/2n)·180°=90°-180°/n. Формулу для определения угла используем для нахождения стороны an. Так как сторона многоугольника равна удвоенной стороне полученного при построении прямоугольного треугольника А1Н1О, подставляя в формулу полученное выражение, получаем формулу для нахождения стороны: an. =2 А1Н1О=2Rcos(90°-180°/n)=2Rsin180°/n. Очевидно, полученное выражение угла и рассматриваемый прямоугольный треугольник А1Н1О помогут также получить формулу для определения радиуса вписанной окружности в n-угольник r=OH1=Rsin(90°-180°/n)=Rcos(180°/n).

В конце видеоурока представлены формулы для нахождения стороны правильного треугольника, 4-угольника, 6-угольника. После подстановки количества сторон для каждого из этих правильных многоугольников, получаем формулы для определения длины стороны: a3=R√3, a4=R√2, a6=R.

Видеоурок «Формулы для определения площади правильного многоугольника, а также его сторон, вычисления радиуса вписанной окружности» предназначен для применения на традиционных уроках математики для повышения эффективности урока. Также данный материал можно рекомендовать ученикам, требующим дополнительного внимания для качественного усвоения материала и изучающим курс самостоятельно. Видеоуроки можно использовать и в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 12196 |
| Номер материала | 753 |