
Урок «Формула Ньютона-Лейбница. Нахождение площадей плоских фигур с помощью интеграла»

Краткое описание документа:
На прошлом уроке мы познакомились с понятием определённого интеграла.
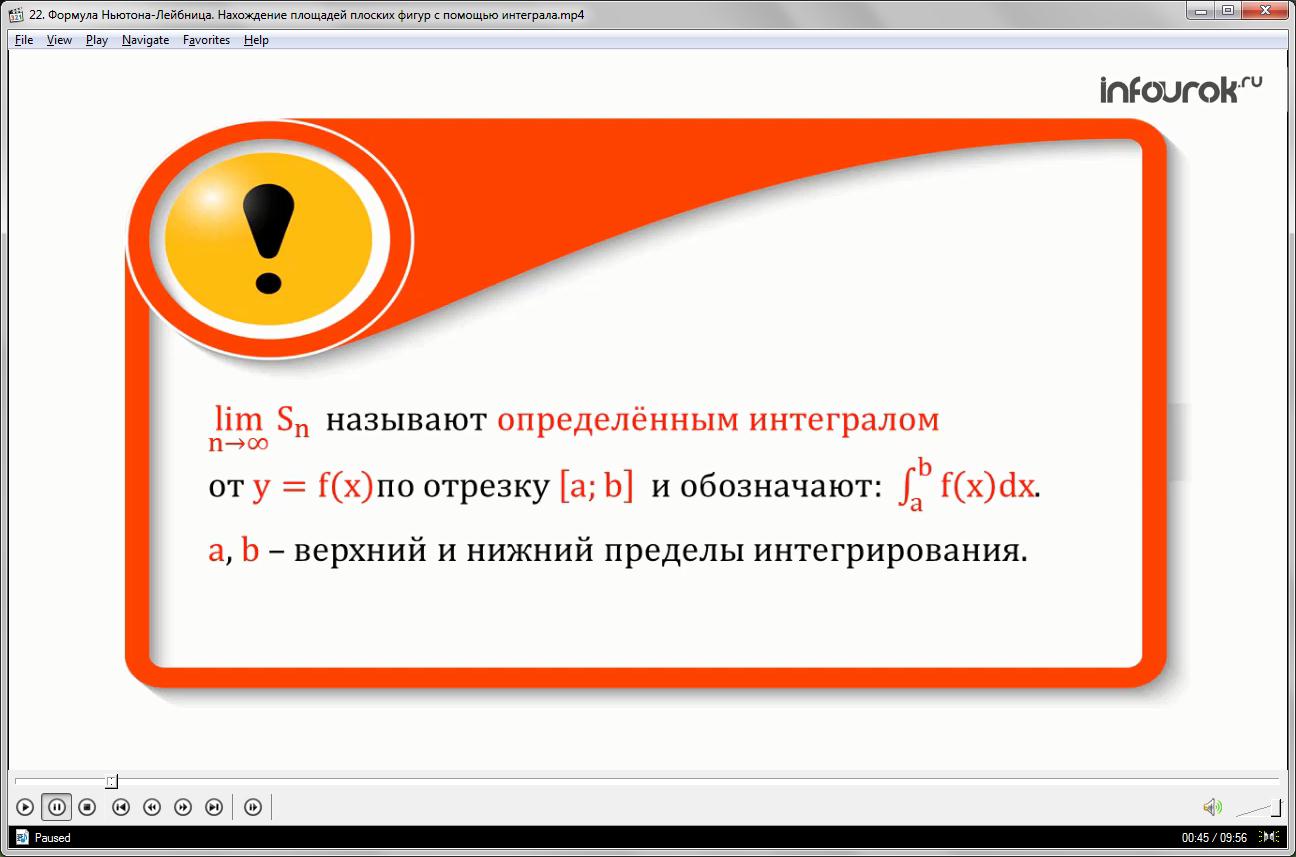
Предел суммы при эн стремящемся к бесконечности называется определённым интегралом от функции (игрек равно эф малое от икс) по отрезку а, бэи обозначается так:
Читается как «интеграл от а до бэ от икс дэ икс».
Числа а и бэ называются верхним и нижним пределами интегрирования.
В курсе математического анализа доказана следующая теорема:
если функция(игрек равен эф от икс) непрерывна на отрезке а, бэ , то справедлива формула:(определённый интеграл от а до бэ эф икс дэ икс равен эф большое от бэ минус эф большое от а), где (эф большое от икс) — первообразная для функции (эф малое от икс).
Данную формулу принято называть формулой Ньютона-Лейбница в честь Исаака Ньютона — английского физика, и Готфрида Лейбница — немецкого философа, которые вывели её независимо друг от друга практически одновременно.
Вместо записи эф от бэ минус эф от а принято записывать так , её называют двойной подстановкой.
Таким образом, формулу Ньютона-Лейбница можно переписать в виде:
Для того чтобы вычислить определённый интеграл, необходимо найти первообразную функции, затем выполнить двойную подстановку.
Рассмотрим применение формулы Ньютона-Лейбница для вычисления определённого интеграла.
Задача 1
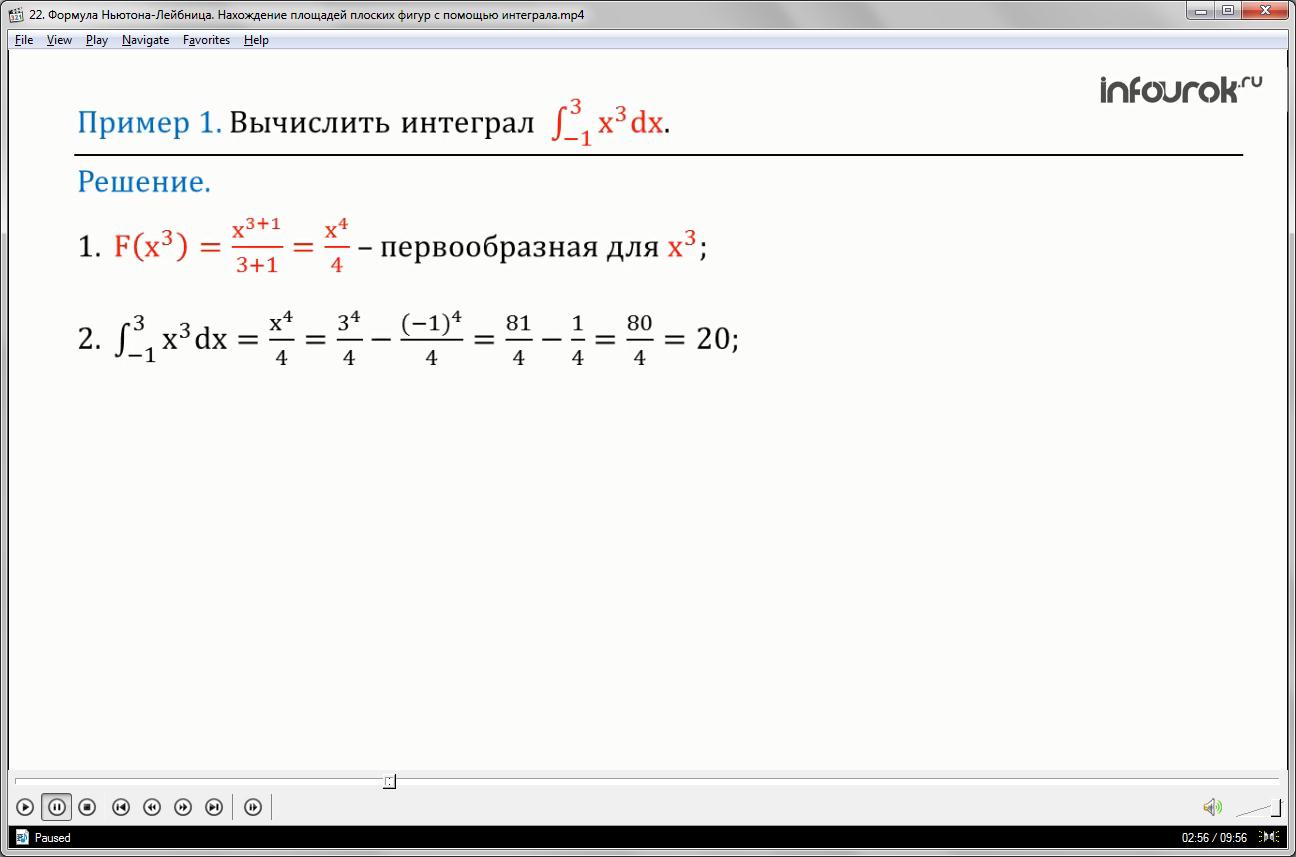
Вычислить интеграл от минус одного до трёх икс в кубе дэ икс:
Решение
1. Вычислим первообразную для икс в кубе.
По формуле первообразной степенной функции имеем: икс в четвёртой, делённое на четыре.
2.Подставим найденную первообразную в формулу Ньютона-Лейбница и выполним двойную подстановку.
Получим: 3 в четвёртой степени, делённое на 4 минус минус один в четвёртой степени, делённое на 4. 3 в четвёртой степени — это 81, (-1) в четвёртой степени — это один.
Имеем, 81 четвёртая минус одна четвёртая — это 80 четвёртых или 20.
Таким образом, интеграл от минус одного до трёх икс в кубе дэ икс равен 20.
Рассмотрим некоторые свойства определённого интеграла.
Свойство 1
Интеграл от суммы равен сумме интегралов.
Свойство 2
Постоянный множитель можно вынести за знак интеграла.
Свойство 3
Если а меньше бэ и бэ меньше це, то сумму интеграла от а до цэ эф от икс дэ икс и интеграла от це до бэ эф от икс дэ икс можно записать в виде интеграла от а до бэ эф от икс дэ икс.
Данное свойство называется аддитивным свойством интеграла, его смысл заключается в том, что площадь криволинейной трапеции равна сумме криволинейных трапеций, из которых она составлена.
Задание 2
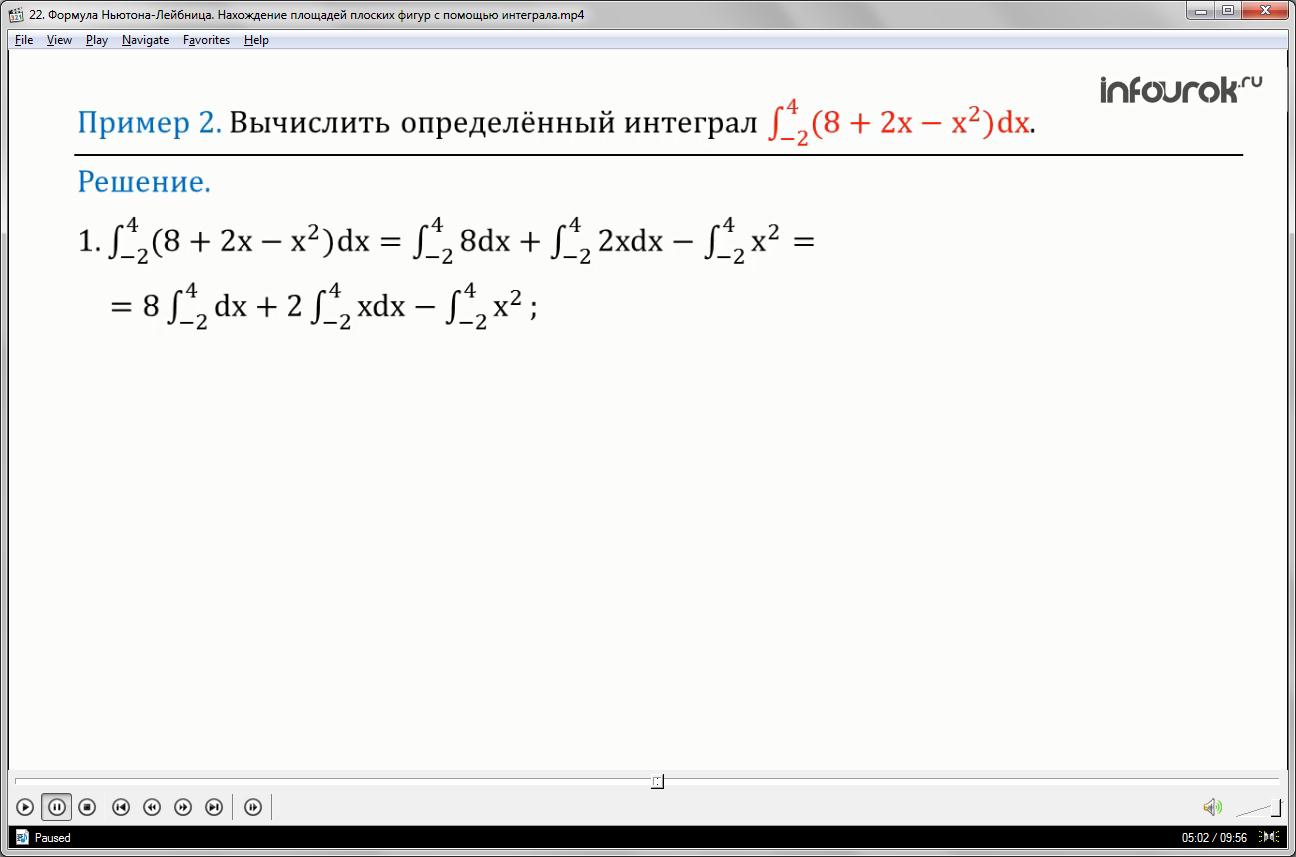
Вычислить определённый интеграл
Решение
1.Воспользуемся свойством интеграла и разобьём данный интеграл на сумму и разность интегралов:
Постоянный множитель можно вынести за знак интеграла, имеем:
2.Найдём первообразную полученной функции применяя табличные значения первообразной
и , затем сократим два и одну вторую при икс в квадрате:
3.Для простоты решения вычислим отдельно каждый интеграл по формуле Ньютона-Лейбница:
Подставим полученные значения интегралов в формулу: =48+12-24=36
Таким образом, значение интеграла от минус двух до четырёх (восемь плюс два икс минус икс в квадрате) дэ икс равно 36.
С помощью определённого интеграла можно вычислять не только площадь криволинейной трапеции, но и плоских фигур более сложного вида.
Итак, площадь S(эс) фигуры, ограниченной прямыми , (икс равно а, икс равно бэ) и графиками функций , (игрек равен эф от икс, игрек равен же от икс), непрерывных на отрезке а, бэ и таких, что (же от икс меньше или равно эф от икс) для всех (икс) из отрезка а, бэ, вычисляется по формуле:
(эс равно интеграл от а до бэ эф от икс минус же от икс дэ икс).
Задание 3
Вычислить площадь фигуры, ограниченной линиями , .
Решение
1. Построим график функции. — прямая, пересекающая ось ординат в точке 6, ось абсцисс в точке -2.На рисунке выделена красным цветом.
2. Построим график функции — парабола, ветви которой идут вниз (так как при икс в квадрате – отрицательный коэффициент). На рисунке график выделен зелёным цветом.
Фигура, площадь которой нужно вычислить, заштрихована.
3. Прямая и парабола пересекаются в точках с координатами (-2;0), (4;6). Абсциссы -2 и 4 будут нижним и верхним пределами интеграла соответственно.
4. Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле.Так как парабола расположена выше прямой, то будем считать, что функция меньше функции .
Вычислим первообразную полученной функции, применяя табличные значения первообразной и , упростим полученное выражение: умножая одну вторую на икс в кубе третьих, получим икс в кубе, делённое на шесть.
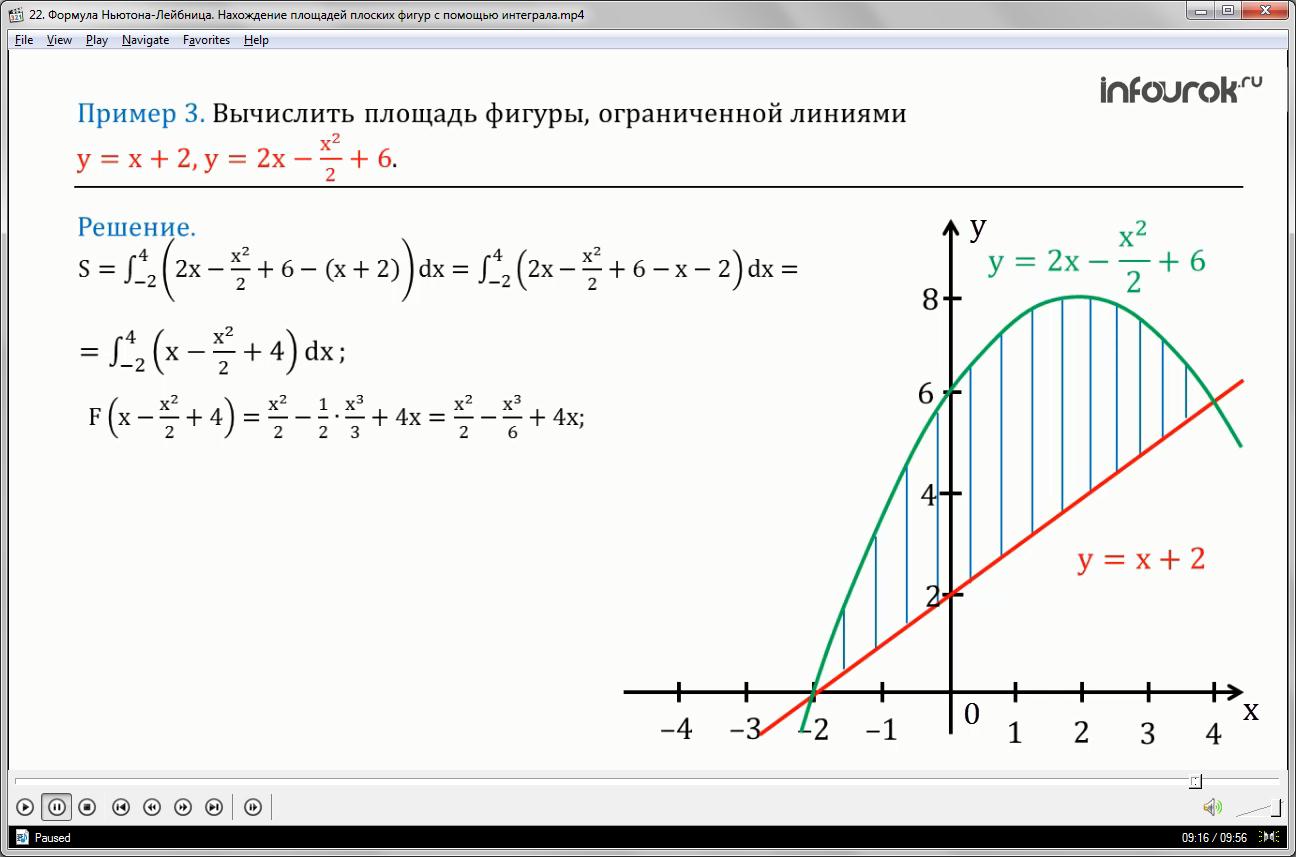
Имеем, икс в квадрате, делённое на два, минус икс в кубе, делённое на шесть, плюс четыре икс.
5.Последовательно подставляя в формулу Ньютона-Лейбница верхний и нижний пределы находим:
Упрощая полученное выражение и приводя подобные слагаемые, получим, что площадь фигуры ограниченной линиями , равна 18.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7531 |
| Номер материала | 1071 |