
Урок «Формула суммы первых n членов арифметической прогрессии»

Краткое описание документа:
Видеоурок «Формула суммы первых n членов арифметической прогрессии» является наглядным пособием для ведения урока алгебр по данной теме. Урок содержит учебный материал, необходимый для освоения методов вычисления суммы первых nчленов данной прогрессии. В ходе урока рассматриваются способы вычисления суммы длинного числового ряда, определяются формулы для быстрого вычисления такой суммы, формируются умения применять эти формулы для решения практических задач с арифметической прогрессией.
В видеоуроке применяются анимационные эффекты, иллюстрации, облегчающие понимание способов решения задач. Данные инструменты наглядности также способствуют удержанию внимания учеников при изучении материала, помогают лучше запомнить материал.
Видеоурок начинается с представления темы. На экране демонстрируется ряд чисел от 1 до 100. Ставится задача вычислить сумму чисел, входящих в данную последовательность. Для лучшей наглядности применения метода решения демонстрируется сложение чисел двух последовательностей с 1 до 100 и в обратном порядке. Отмечается, что при сложении крайних членов последовательности и дальше, приближаясь к середине, они попарно составляют в сумме 101. Всего таких пар будет 100. Отсюда сумма двух последовательностей составит 2S=101·100. При вычислении суммы 100 членов одной последовательности получается S=101·100/2=5050.
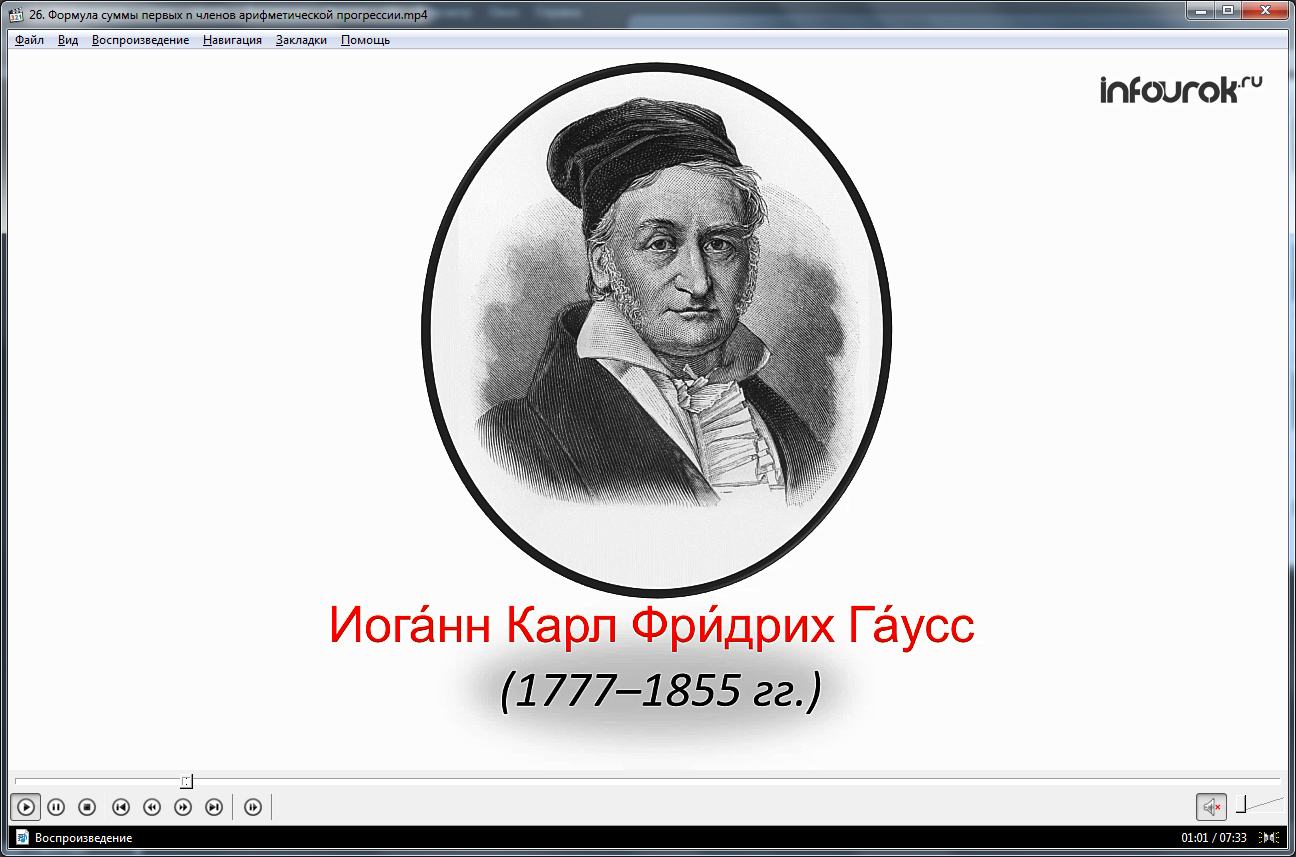
Рассмотренная особенность числового ряда, помогающая проводить более быстрые вычисления, имеет историю, связанную с известным математиком Иоганном Карлом Фридрихом Гауссом. Для учеников проводится небольшой экскурс в историю математики, рассказывая как этот математик, будучи учеником, подметил, что крайние члены последовательности составляют в сумме 101 и в отличие от других учеников, провел быстрые вычисления. Также отмечается, что аналогично рассуждая, можно найти сумму арифметической прогрессии сколь угодно длинной. Для этого используется далее рассмотренная формула.
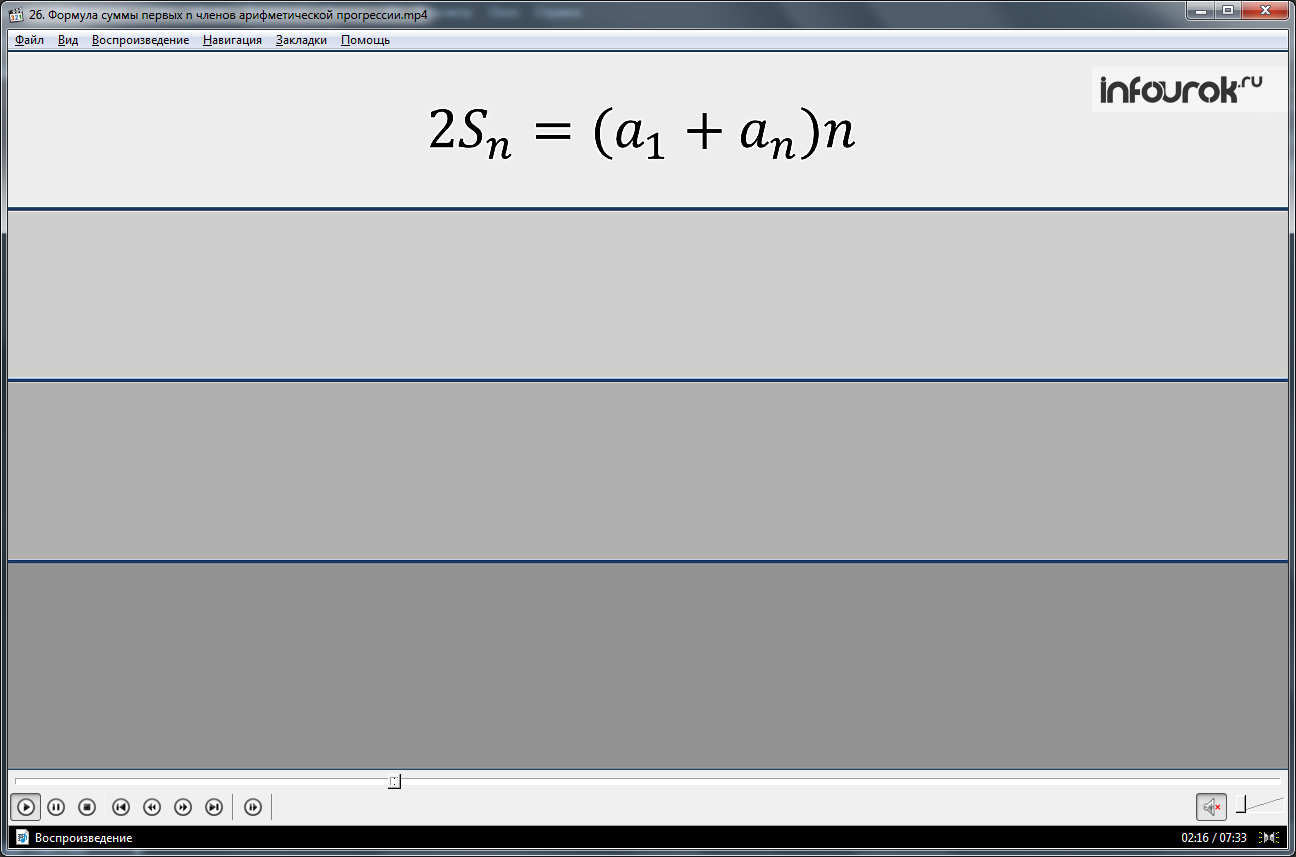
Вводится обозначение суммы членов Sn. Аналогично ходу рассуждения при вычислении суммы прогрессии от 1 до 100, рассматривается общий случай суммы членов прогрессии от а1 до аn. Для этого на экране представлено формулами две суммы от а1 до аn и в обратном порядке. Если сложить второй член первой и второй прогрессии, получается, что эта сумма будет равна сумме первых членов: а2+аn-1=(а1+d)+(аn-d)= а1+аn. Аналогично проверяется равенство суммы всех пар, сложенных таким образом. И отмечается, что таких пар будет n. В результате сложения двух прогрессий получится 2Sn=(а1+аn) n. Отсюда формула суммы определяется Sn=(а1+аn) n/2. Также определяется другой вид данной формулы, который чаще используется при решении задач, где необходимо вычислить сумму некоторого числа членов прогрессии. В этой формуле сумма выражена через первый член прогрессии и разность: Sn=(2а1+d(n-1)/2)n.
Рассматривается пример, в котором описывается вычисление суммы 40 членов арифметической прогрессии (аn), которая представлена числами 6; 6,5… очевидно, что это прогрессия с разностью d=0,5 и первым членом а1=6. Для нахождения 40-го члена прогрессии используется формула а40= а1+d(n-1). После подстановки значений находим а40=25,5. При подстановке найденного значения в формулу для нахождения суммы 40 членов прогрессии, получаем S40=(6+25,5)·40/2=630. Для вычисления суммы по второй формуле не требуется отдельного вычисления 40-го члена: S402·6+0,5(40-1)/2=630.
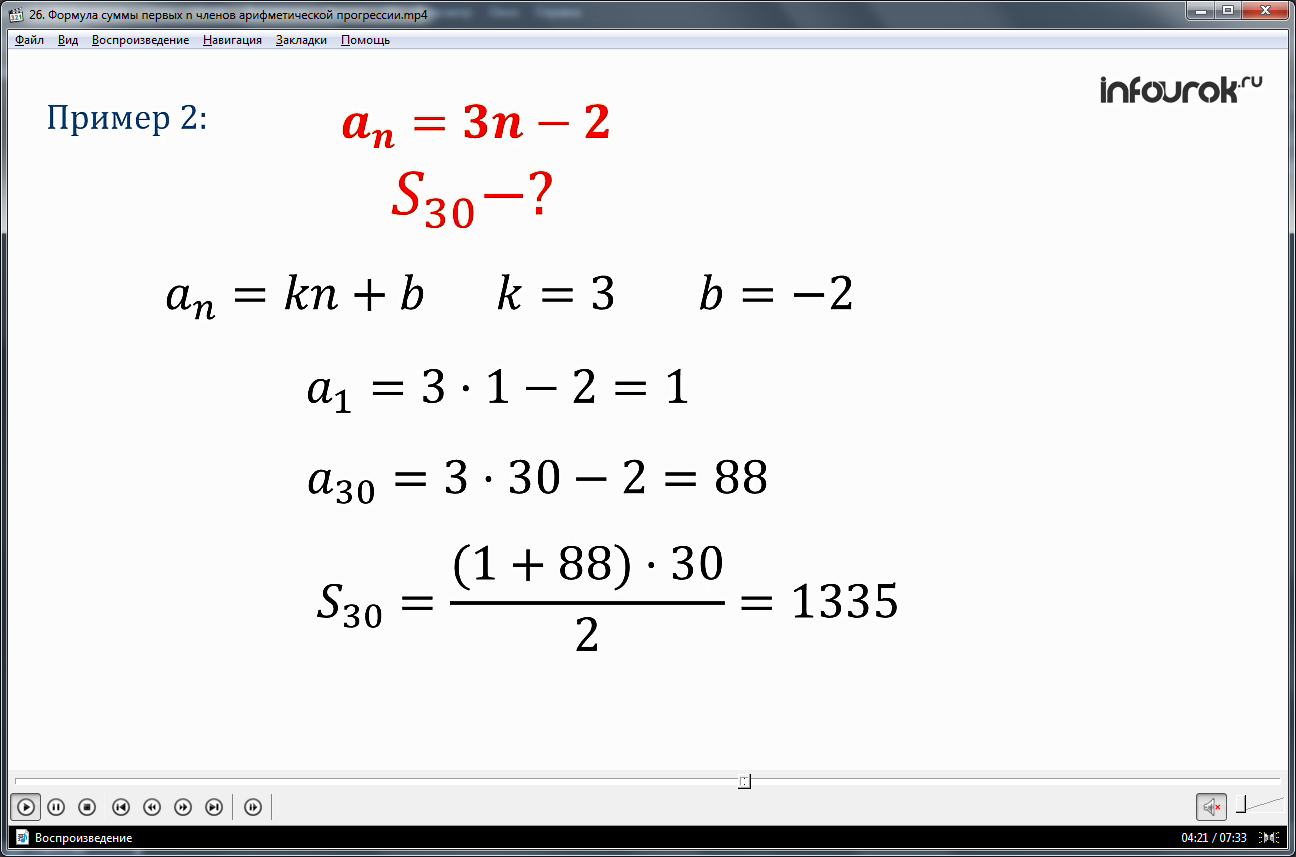
Во втором примере используется представление члена арифметической прогрессии в виде аn=kn+b. Арифметическая прогрессия представлена общим видом члена прогрессии аn=3n-2. Необходимо найти сумму 30-ти членов данной прогрессии. Так как член прогрессии определяется формулой вида аn=kn+b с k=3 и b=-2, ее первый член будет равен а1=3·1-2=1, 30-й равен а30=3·30-2=88. А сумма 30-ти первых членов по формуле суммы, выраженной через первый и последний член, составляет S30=(1+88)·30/2=1335.
В третьем примере необходимо найти сумму натуральных чисел, которые кратны 8 и не превосходящих 150. Решения данной задачи удовлетворяют основным условиям: аn=8n и 8n<=150. Из неравенства получаем, что n<=18+3/4. Это значит. Что необходимо найти сумму 18-ти членов прогрессии, в которой первый член а1=8, а18=8·18=144. Подставляя значения в формулу для поиска суммы, получаем S18=(8+144)·18/2=1368.
Продолжая тему последовательностей, дается информация о числах, которые возникают в процессе решения практических задач. Примером служат числа, возникавшие в процессе рассмотрения количества фигур, образованных геометрическими фигурами. Таким образом формируются числовые последовательности треугольных чисел 1, 3, 6, 10…, квадратных чисел 1, 4, 9, 16… пятиугольных чисел 1, 5, 12, 22, демонстрируемые на экране.
Рассматривается последовательность треугольных чисел. Формулы, определяющие член данной последовательности an=(1+n)n/2. Последовательность состоит из членов: а1=1, а2=1+2, а3=1+2+3, аn=1+2+3+..+n.
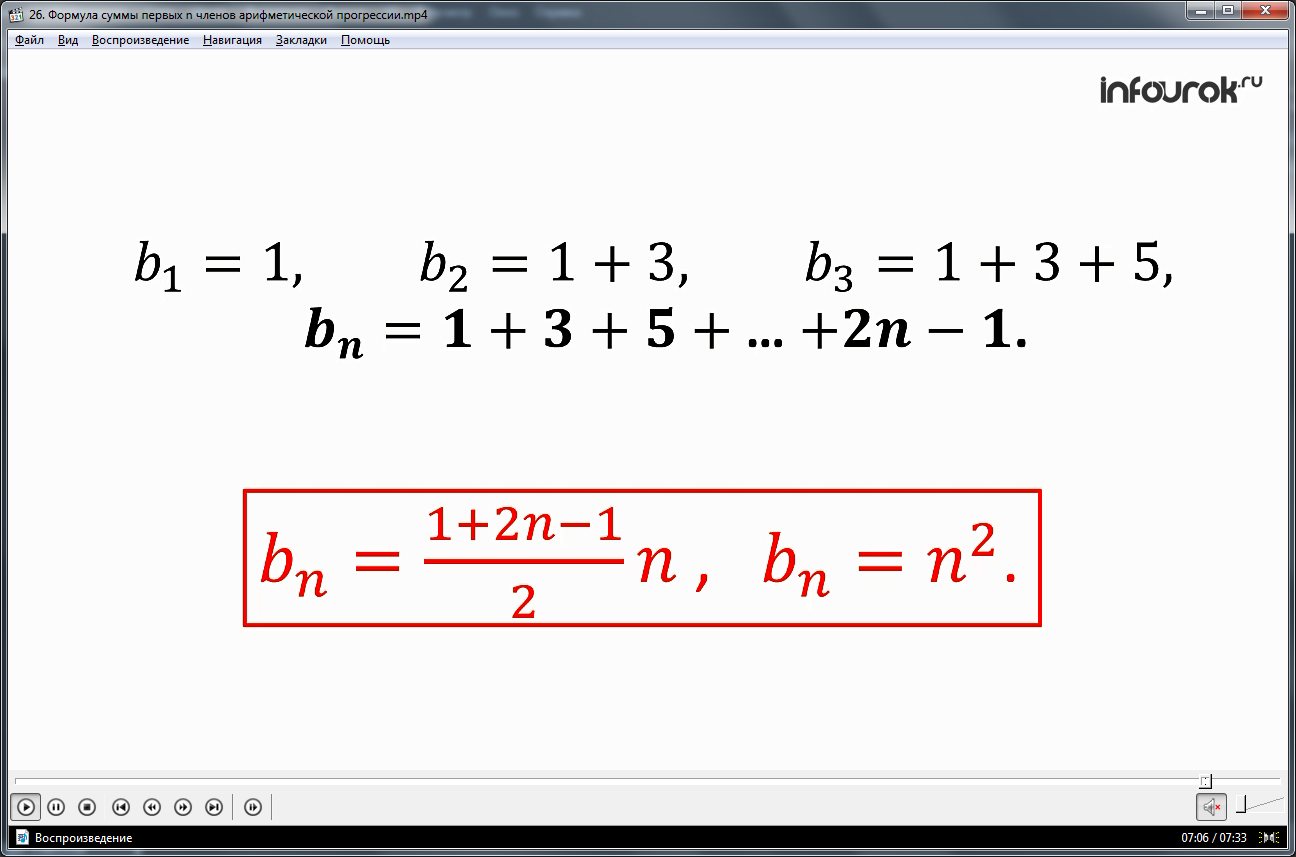
Последовательность квадратных чисел состоит из членов, которые образуются суммами нечетных натуральных чисел: b1=1, b2=1+3, b3=1+3+5, bn=1+3+5+..+2n-1. Таким образом, данная последовательность представляется общей формулой члена прогрессии bn=(1+2n-1)n/2, или bn=n2.
Последней рассматривается последовательность пятиугольных чисел. Она образуется суммами ряда чисел c1=1, c2=1+4, c3=1+4+7, cn=1+4+7+..+(1+3(n-1)). Данную последовательность можно представить общей формулой cn=(1+1+3(n-1)n/2, или cn=3(n-1)n/2.
Видеоурок «Формула суммы первых n членов арифметической прогрессии» может использоваться для наглядности представления учебного материала на уроке алгебры, а также в качестве отдельной части урока, не требующей сопровождения учителя. Также материал может быть полезен учителю при дистанционном обучении, для самостоятельного рассмотрения учеником.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7503 |
| Номер материала | 670 |