
Урок "Формулы понижения степени"

Краткое описание документа:
Тригонометрия – это один из важнейших разделов, который изучается в курсе алгебры в 10 классе. Ему уделяется достаточно щедрое количество уроков. Ведь для того, чтобы как следует понять тригонометрию и в теории и на практике, необходимо постоянно решать огромное количество примеров, которые укрепят теорию и позволят расширить навыки выполнения той или иной работы: домашней, контрольной, самостоятельной или просто классной.
Видеурок имеет грамотное составление, все последовательно и логично. Структура является четкой, текст составлен грамотно и понятно для школьного уровня. Данный ресурс поможет сделать процесс изучения темы «Формулы понижения степени» намного интереснее и эффективное. Благодаря визуализации, ученики смогут лучше запомнить формулы, а сопровождению спокойным голосом диктора видеозаписи, запоминание ускориться.
Материал, который рассказывается и рассматривается в ресурсе, составлен специалистами таким образом, чтобы полностью раскрыть тему, не упустить ни один важный момент. Это говорит о том, что его можно смело использовать при составлении планов-конспектов к урокам, что делают молодые учителя в обязательном порядке.
Ранее были рассмотрены уже формулы косинуса, синуса, тангенса суммы аргументов, двойного аргумента. Котангенс в отдельности не рассматривался, ведь его всегда можно представить в виде обратной дроби к тангенсу. В этой видеозаписи будут рассматриваться еще одни важные формулы, с помощью которых можно понизить степень.
В первую очередь выводятся формулы понижения квадрата. Мы видим, как просто можно избавиться от второй степени в косинусе и синусе. Для того чтобы школьники могли понять, откуда взялись эти формулы, следующим шагом диктор подробно рассказывает, все шаги. В первую очередь, стоит вспомнить основную формулу в тригонометрии, гласящую о том, что сумма квадрата синуса и косинуса дает нам единицу. Из этого тождества можно вывести в отдельности и квадрат синуса, и косинуса. Вспомнив формулу косинуса и синуса двойного аргумента, можно понять, откуда появились новые правила.
Заметно, что при выполнении любого шага, мы обращаемся к материалу, который ранее был изучен. Это указывает на важность и взаимосвязанность тем в тригонометрии. Ни в коем случае нельзя упускать те или иные темы и приступить к новым. Материал станет непонятным, ведь будет неизвестно, откуда появились те или иные значения и преобразования. Так как тригонометрия содержит большое количество формул, без которых двигаться дальше невозможно, стоит постепенно их запоминать и изучать новые. Также закреплять материал нужно на практике и получать новые навыки, которые пригодятся в дальнейшем при написании контрольных и семестровых работ.
Видеоурок «Формулы понижения степени» после рассмотрения формул переходит к практическому разбору примеров, что, как было уже сказано, очень важно. Примеры будут понятны, при внимательном просмотре самостоятельно либо вместе с учителем.
В первом примере необходимо найти значение некоторого выражения при определенных условиях. При его решении используется формула понижения градуса косинуса. Чтобы она была на виду, в видеозаписи выводится с правой стороны. Таким образом, у учеников будет возможность повторить и пользоваться ею.
После этого диктор предлагает решить похожий пример, в котором используется формула понижения степени синуса. Его школьники могут самостоятельно решить. Если они поняли предыдущий пример, то справятся и с этим.
В итоге приводится еще один более сложный пример. При ее решении используется формула тангенса. Диктор подробно объясняет решение, после чего выводится ответ.
Видеоурок за короткое время расскажет полностью о том, что такое формулы понижения степени и как ими необходимо пользоваться на практике.
ТЕКСТОВАЯ РАСШИФРОВКА:
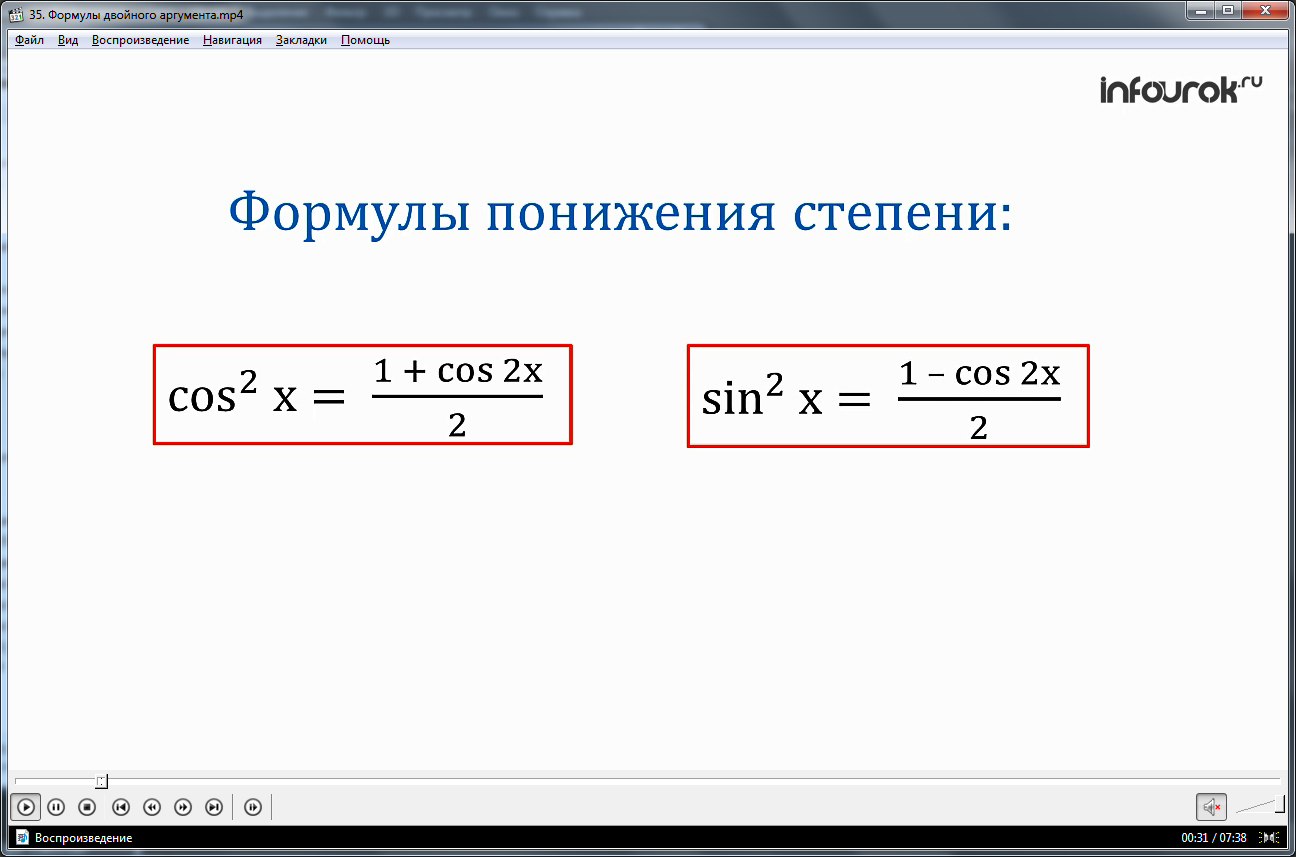
Формулы понижения степени
Формулы
cos2 х = (квадрат косинуса икс равен полу-сумме единицы и косинуса двойного аргумента).
sin2 х = (квадрат синуса икс равен полу-разности единицы и косинуса двойного аргумента).
называют формулами понижения степени.
Выведем эти формулы:
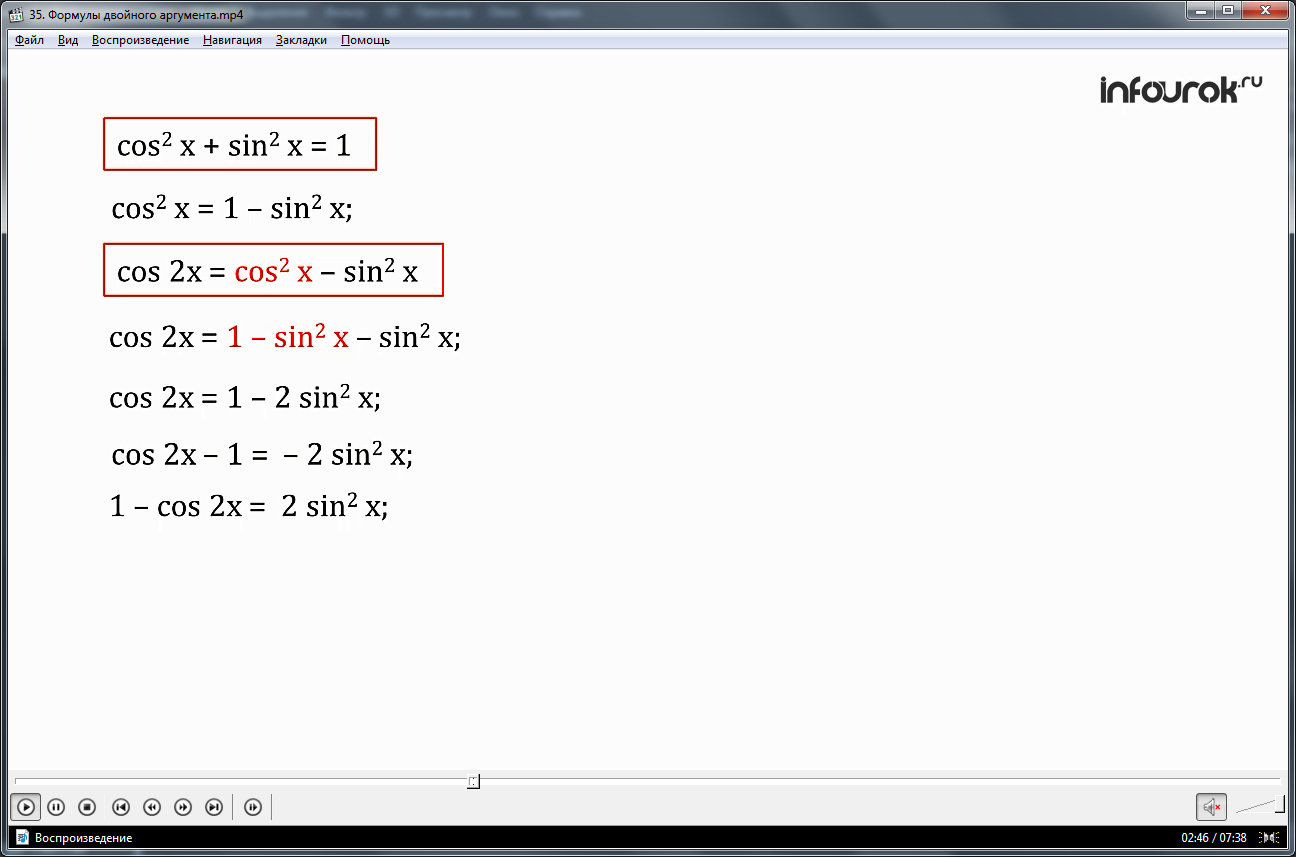
Из формулы cos2 х + sin2 х= 1, из найдем sin2 х:
sin2 х= 1–cos2 х
В формуле cos 2x= cos2 х – sin2 х, значение sin2 х заменим на 1– cos2х и получим cos2 х – (1– cos2 х)
при раскрытии скобок получаем cos2 х – 1+ cos2 х
так как cos2 х + cos2 х в сумме 2cos2 х
получаем, что cos 2x = 2 cos2 х – 1.
cos 2x = cos2 х – sin2 х = cos2 х – (1–cos2 х) = 2 cos2 х – 1.
Отсюда выражаем cos2 х
cos 2x +1 = 2 cos2 х
cos2х = (квадрат косинуса икс равен полу-сумме единицы и косинуса двойного аргумента).
Мы вывели первую формулу понижения степени для cos2 х.
Аналогично выведем и вторую формулу понижения степени для sin2 х:
Из формулы cos2 х + sin2 х= 1, из найдем cos2 х:
cos2 х = 1 - sin2 х
В формуле cos 2x= cos2 х – sin2 х, значение cos2 х:
заменим на 1 - sin2 х
и получим 1 - sin2 х– sin2 х
Так как –sin2х –sin2х в сумме даст –2 sin2 х,
получаем, что cos 2x = 1 –2 sin2 х.
Отсюда выражаем sin2 х:
переносим единицу с противоположным знаком
cos 2x–1 = –2 sin2 х
меняем знаки на противоположные
1- cos 2x = 2 sin2 х
делим на 2 обе части равенства:
sin2 х = (квадрат синуса икс равен полу-разности единицы и косинуса двойного аргумента).
Запомните, формулы, которые мы получили, называют формулами понижения степени.
Такое название было дано из-за того, что в левой части обоих тождеств содержится вторая степень косинуса и синуса, а в правой части – первая степень, т.е наблюдается понижение степени.
Рассмотрим решение примеров с применением формул понижения степени.
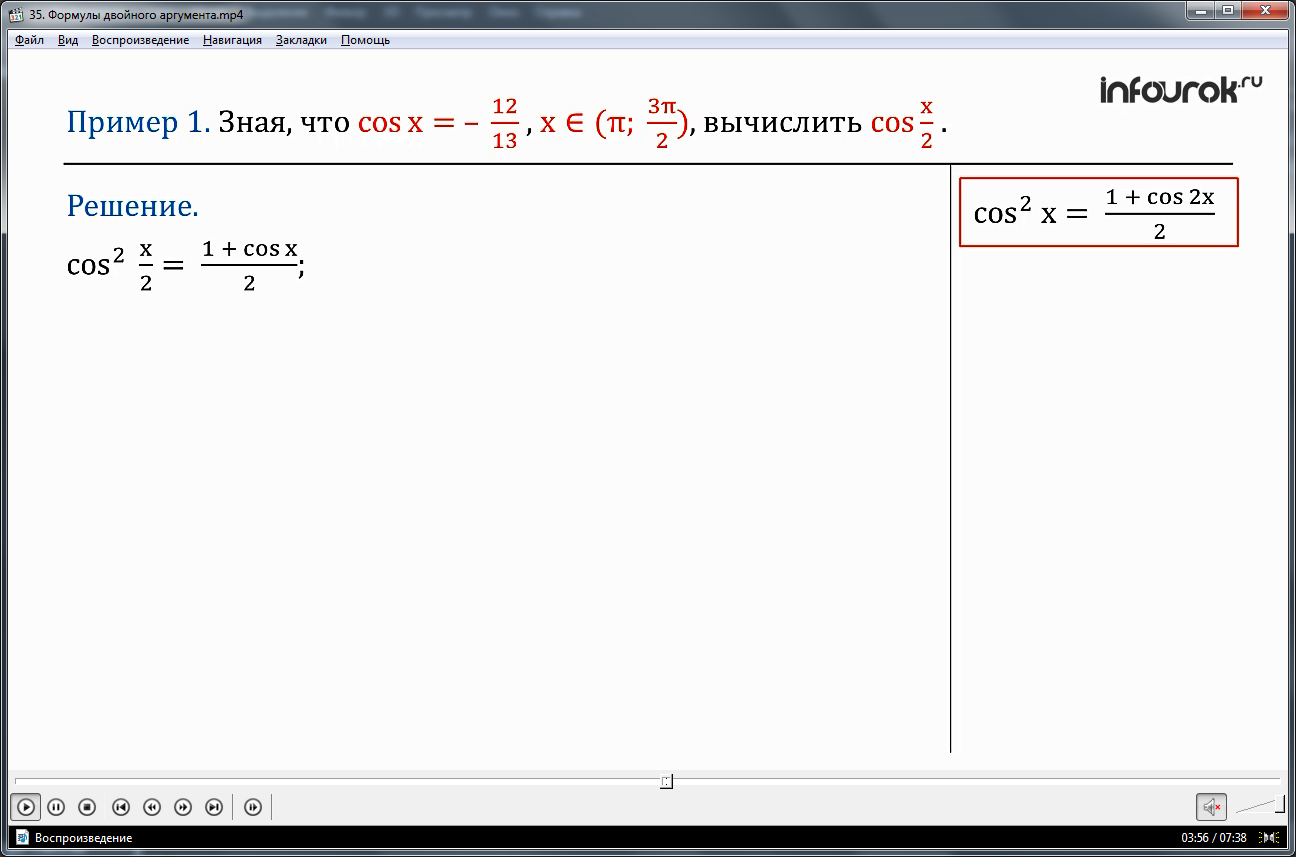
ПРИМЕР 1. Зная, что cosx= – и хϵ(π;) (икс принадлежит промежутку от пи до трех пи на два), вычислить cos.
Решение.
Будем использовать формулу понижения степени
квадрат косинуса икс cos2х =, так как , то получим:
cos2 =.
по условию cosx= – подставив данные в формулу имеем:
cos2 = , сделав вычисления в правой части выражения, получим
cos2= , извлечем корень квадратный из , получим
По условию π х , следовательно, . Это значит, что аргумент икс, деленное на два принадлежит второй четверти, где косинус отрицательный. Поэтому cos = − .
Ответ: cos = − .
ПРИМЕР 2. Зная, что cosx= – и хϵ (π;)
(икс принадлежит промежутку от пи до трех пи на два), вычислить sin.
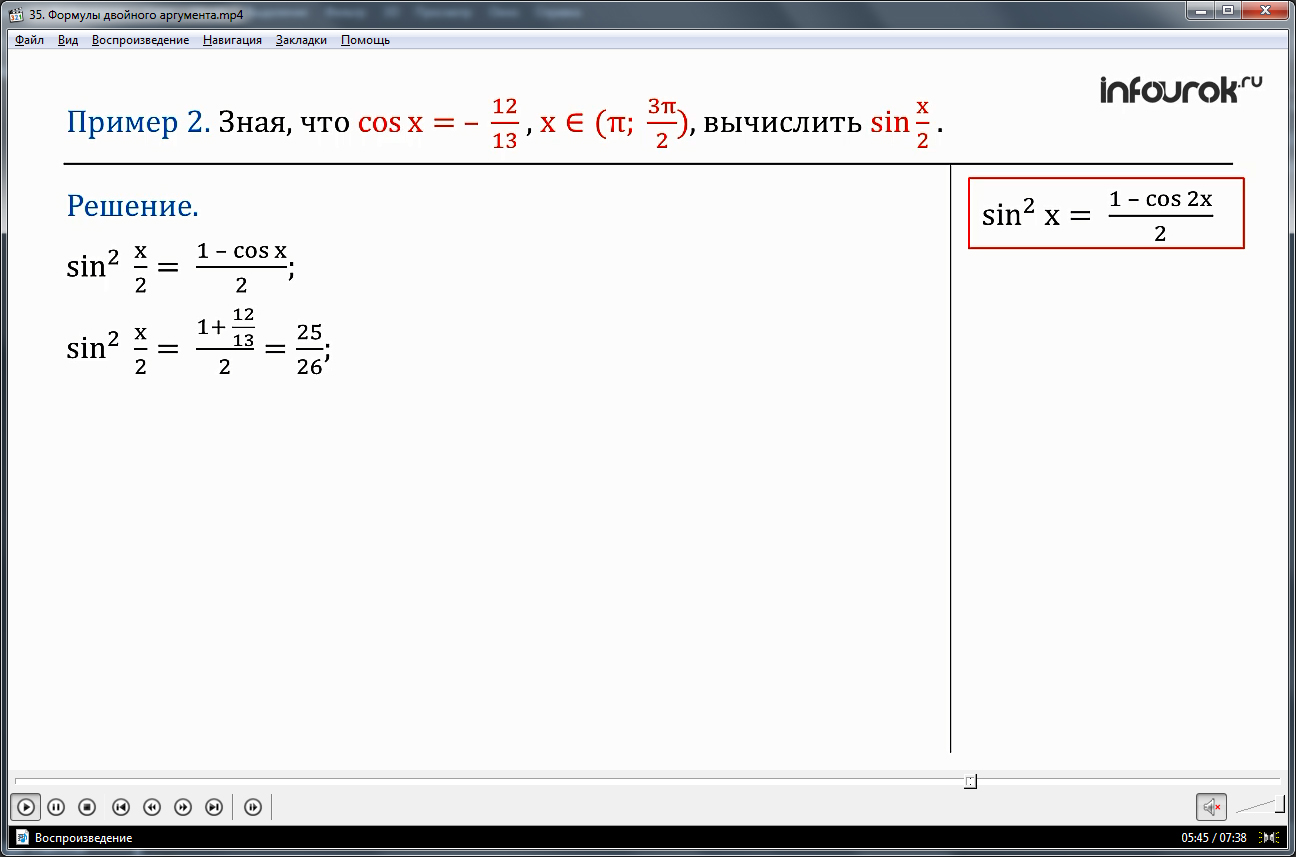
Решение. Будем использовать формулу понижения степени sin2 х =
sin2 =, так как по условию cosx= –
Имеем: sin2 = = , извлечем корень квадратный и получим
sin = .
По условию π х , следовательно, . Это значит, что аргумент икс, деленное на два принадлежит второй четверти, где синус положительный. Поэтому sin = .
Ответ: sin = .
ПРИМЕР 3. Зная, что cosx= – и хϵ(π;) (икс принадлежит промежутку от пи до трех пи на два), вычислить tg.
Решение. Зная, что тангенс икс – это отношение синуса икс к косинусу икс, имеем
tg
в примерах 1 и 2 мы нашли, что sin = и cos = − , поэтому
= :(− ) =–5 .
Ответ: tg =–5.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10363 |
| Номер материала | 848 |