
Урок "Функции y = tgx, y = ctgx, их свойства и графики"

Краткое описание документа:
В этом видеуроке рассмотрены свойства функций у = tgx, y = ctgx, показано, как построить их графики.
Видеоурок начинается с рассмотрения функции у = tgx.
Выделены свойства функции.
1) Областью определения функции у = tgxназываются все действительные числа, за исключением х = π/2 +2 πk. Т.е. на графике нет точек, которые принадлежат прямой х = π/2 и х = – π/2, а также х = 3π/2 и так далее (с той же периодичностью). Значит, график функции у = tgxбудет состоять из бесконечного множества ветвей, которые будут находиться в промежутках между прямыми х = –3π/2 и х = –π/2 , х = –π/2 и х = π/2 и так далее.
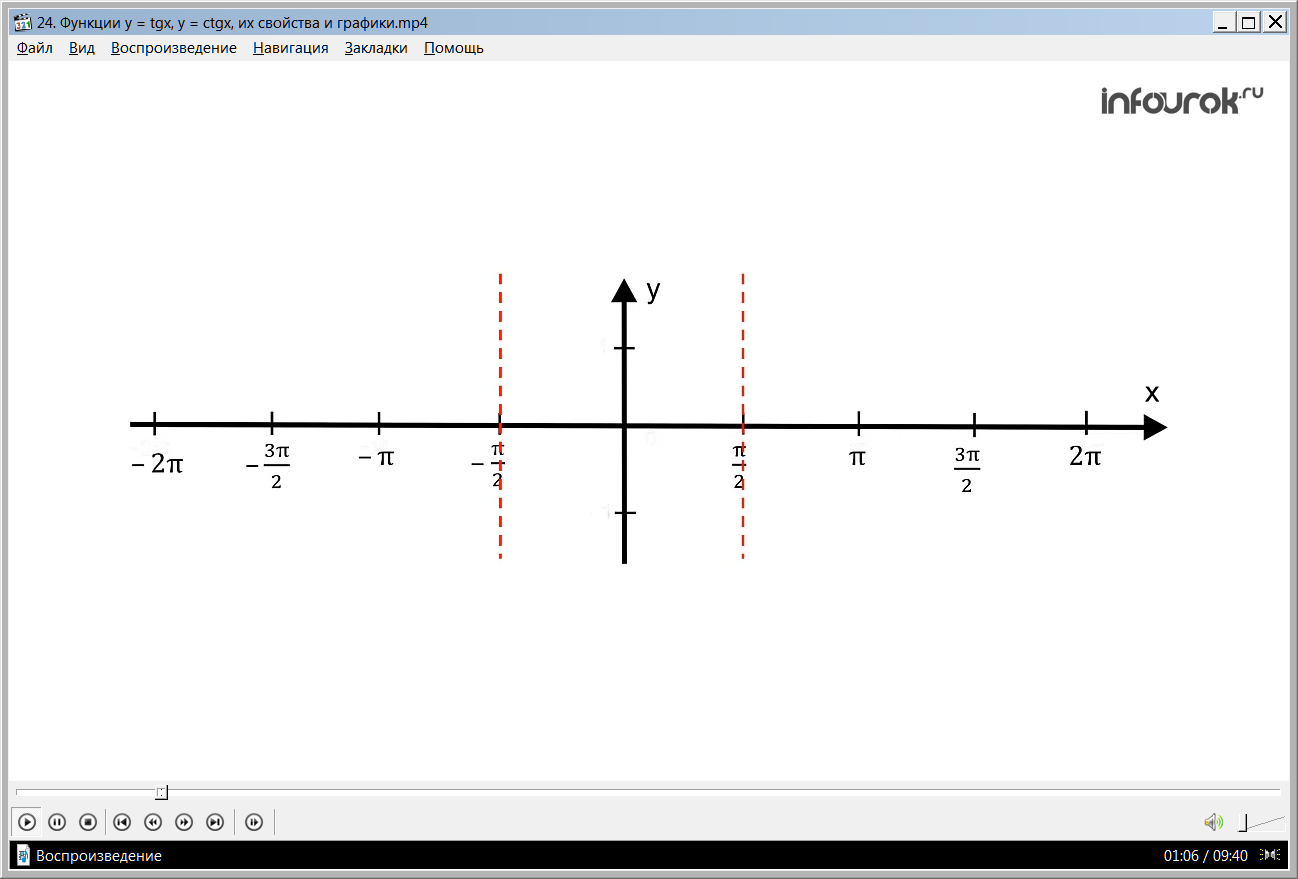
2) Функция у = tgxявляется периодической, где основной период равенπ. Это подтверждает равенство tg (x – π)=tg x = tg (x + π).Эти равенства изучались ранее, автор предлагает ученикам вспомнить их, указывая, что для любого допустимого значения tсправедливы равенства:
tg (t + π) = tg t, и ctg (t + π) =ctg t. Следствием этих равенств является то, что, если построена одна ветвь графика функции у = tgxв промежутке между прямыми х = –π/2 и х = π/2 , то остальные ветви можно получить путем сдвига этой ветви по оси х на π, 2π и так далее.
3) Функция у = tgxявляется нечетной, т.к. tg (–x) = – tg x.
Далее перейдем к построению графика функции у = tgx. Как следует из свойств функции, описанных выше, функция у = tgx периодическая и нечетная. Поэтому достаточно построить часть графика – одну ветвь в одном промежутке, а затем воспользоваться симметрией для переноса. Автор приводит таблицу, в которой рассчитываются значения tgx при определенных значениях xдля более точного построения графика. Данные точки отмечаются на оси координат и соединяются плавной линией. Т.к. график симметричен относительно начала координат, то строится такая же ветвь, симметричная началу координат. В результате получаем одну ветвь графика у = tgx. Далее с помощью сдвига по оси х наπ, 2 πи так далее получается график у = tgx.
График функции у = tgx называется тангенсоида, а три ветви графика, показанные на рисунке – главные ветви тангенсоиды.
4) Функция у = tgx на каждом из промежутков (– + ; + ) возрастает.
5) График функции у = tgx не имеет ограничений сверху и снизу.
6) Функция у = tgx не имеет наибольшего и наименьшего значения.
7) Функция у = tgx непрерывна на любом промежутке (-–π/2+π;π/2+π). Прямая π/2+π называется асимптотой графика функции у = tgx, т.к. в этих точках график функции прерывается.
8) Множеством значений функции у = tgxназываются все действительные числа.
Далее в видеоуроке дается пример: решить уравнение с tgx. Для решения построим 2 графика функции у и найдем точки пересечения этих графиков: это бесконечное множество точек, абсциссы которых отличаются на πk. Корнем данного уравнения будет х = π/6 +πk.
Рассмотрим график функции у = ctgx. График функции можно построить двумя способами.
Первый способ предполагает построение графика аналогично построению графика функции у = tgx. Построим одну ветвь графика функции у = сtgxв промежутке между прямыми х = 0и х = π. Затем с помощью симметрии и периодичности построим другие ветви графика.
Второй способ более простой. График функции у = сtgxможно получить путем преобразования тангенсоиды с помощью формулы приведения сtgx = – tg (x + π/2). Для этого сдвинем одну ветвь графика функции у = tgxвдоль оси абсцисс на π/2вправо. Остальные ветви получаем путем сдвига этой ветви по оси х наπ, 2π и так далее. График функции у = ctgx называется также тангенсоида, а ветвь графика в промежутке (0;π) – главная ветвь тангенсоиды.
ТЕКСТОВАЯ РАСШИФРОВКА:
Мы рассмотрим свойства функции у = tg x ( игрек равно тангенс икс), у = ctg x( игрек равно котангенс икс), построим их графики. Рассмотрим функцию y = tgx
Прежде, чем строить график функции у = tg x, запишем свойства этой функции.
СВОЙСТВО 1. Областью определения функции у = tg x являются все действительные числа, кроме чисел вида х = + πk (икс равен сумме пи на два и пи ка).
Это значит, что на графике этой функции нет точек, которые принадлежат прямой х = ( получаем, если k= 0 ка равно нулю) и прямой х = ( икс равно минус пи на два ) (получаем, если k= - 1 ка равно минус одному), и прямой х = ( икс равно три пи на два ) (получаем, если k= 1 ка равно одному) и т. д. Значит график функции у = tg x будет состоять из бесконечного множества ветвей, которые будут находиться в промежутках между прямыми. А именно в полосе между х = и х =- ; в полосе х =- и х = ; в полосе х = и х = и так до бесконечности.
СВОЙСТВО 2. Функция у = tg x является периодической с основным периодом π. (Так как справедливо двойное равенство
tg( x– π) = tgx = tg (x+π) тангенс от икс минус пи равен тангенсу икс и равен тангенсу от икс плюс пи). Это равенство мы рассматривали при изучении тангенса и котангенса. Напомним его:
Для любого допустимого значения t справедливы равенства:
tg (t + π)= tgt
ctg (t + π) = ctgt
Из этого равенства следует, что, построив ветвь графика функции у = tg x в промежутке от х =- и х = , мы получим остальные ветви путем сдвига построенной ветви по оси Х на π, 2π, и так далее.
СВОЙСТВО 3. Функция у = tg x является нечетной функцией, так как справедливо равенство tg ( - x) = - tg x.
Построим график функции у = tg x
Так как эта функция периодическая, состоит из бесконечного множества ветвей (в полосе между х = и х = , а также в полосе между х = и х = и т.д.) и нечетная, то построим по точкам часть графика на промежутке от нуля до пи на два (), затем воспользуемся симметрией начала координат и периодичностью.
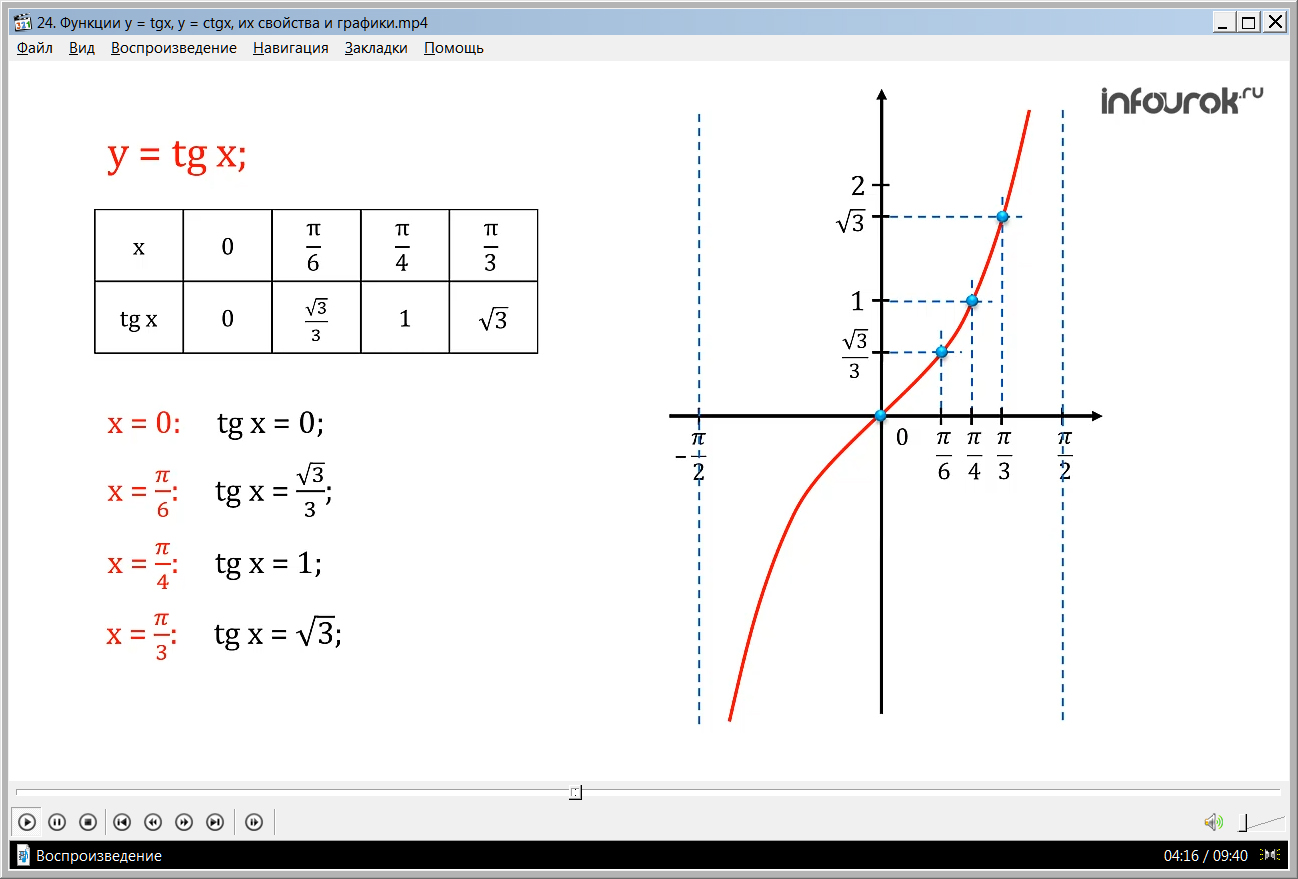
Построим таблицу значений тангенса для построения графика.
Находим первую точку: зная, что при х = 0 tg x = 0( икс равном нулю тангенс икс тоже равен нулю); следующая точка: при х = tg x = ( икс равном пи на шесть тангенс икс равен корень из трех на три); отметим следующие точки: при х = tg x = 1 (икс равном пи на четыре тангенс икс равен единице), а при х = tg x = ( икс равном пи на три тангенс икс равен корню квадратному из трех). Отметив полученные точки на координатной плоскости и соединим их плавной линией (рис. 2).
Так как график функции симметричен относительно начала координат, то построим такую же ветвь симметрично начала координат. (рис.3).
И, наконец, применив периодичность, получим график функции у = tg x.
Мы построили ветвь графика функции у = tg x в полосе от х =- и х = . Строим остальные ветви путем сдвига построенной ветви по оси Х на π, 2π, и так далее.
Построенный график называется тангенсоида.
Изображенную на рисунке 3 часть тангенсоиды называют главной ветвью тангенсоиды.
На основании графика запишем еще свойства этой функции.
СВОЙСТВО 4. Функция у = tg x возрастает на каждом из промежутков (от минус пи на два плюс пи ка до пи на два плюс пи ка).
СВОЙСТВО 5. Функция у = tg x не ограничена ни сверху, ни снизу.
СВОЙСТВО 6. Функция у = tg x не имеет ни наибольшего, ни наименьшего значений.
СВОЙСТВО 7. Функция у = tg x непрерывна на любом интервале вида ( от минус пи на два плюс пи ка до пи на два плюс пи ка).
Прямая вида х = + πk (икс равно сумме пи на два и пи ка) является вертикальной асимптотой графика функции, так как в точках вида х = + πk функция терпит разрыв.
СВОЙСТВО 8. Множеством значений функции у = tg x являются все действительные числа, то есть ( е от эф равно промежутку от минус бесконечности до плюс бесконечности).
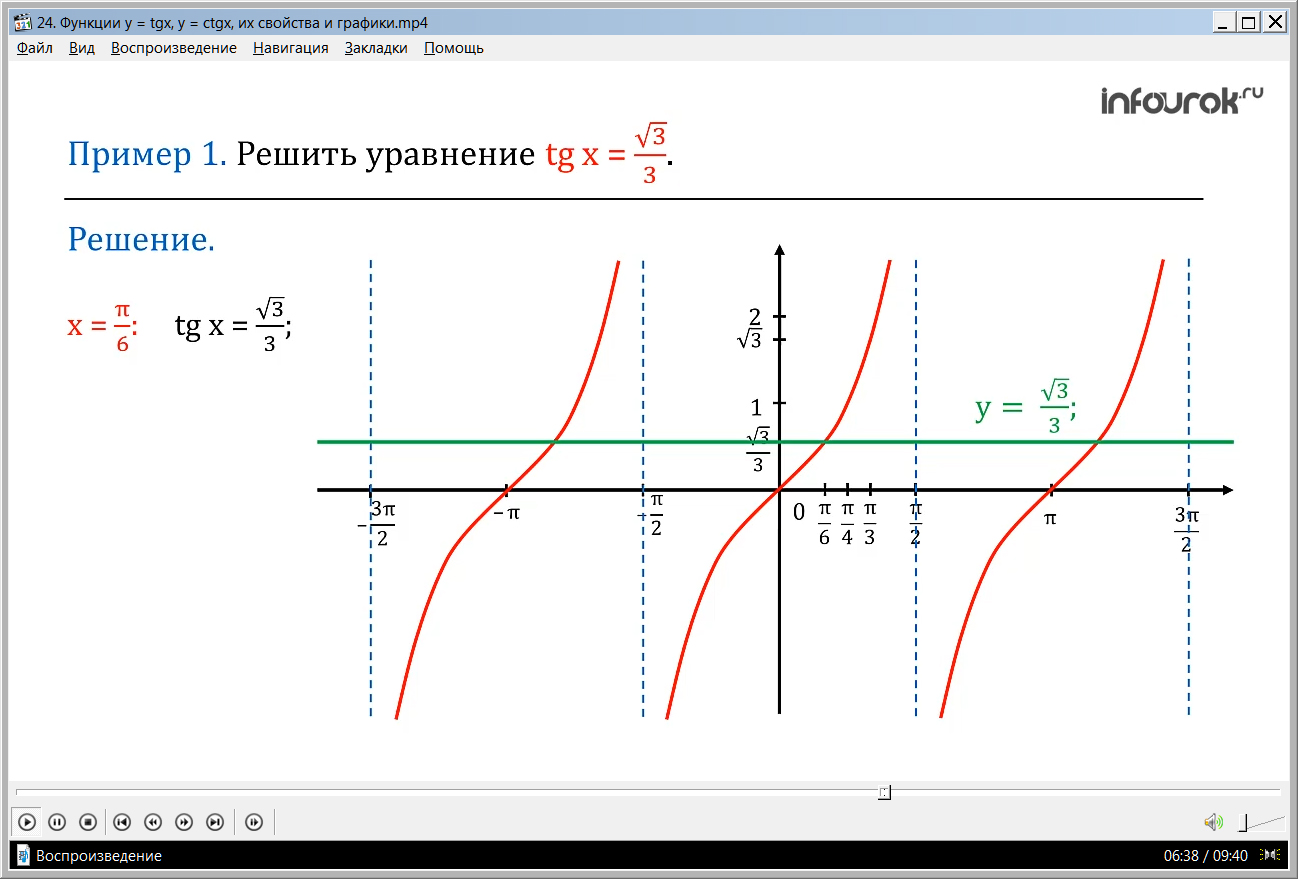
ПРИМЕР 1. Решить уравнение tg x = (тангенс икс равен корень из трех на три).
Решение. Построим в одной системе координат графики функций у = tg x
(игрек равен тангенсу икс) и у = ( игрек равен корню из трех, деленному на три).
Получили бесконечно много точек пересечения, абсциссы которых отличаются друг от друга на πk ( пи ка).Так как tg x = при х = , то абсцисса точки пересечения на главной ветви равна ( пи на шесть).
Все решения данного уравнения запишем формулой х = + πk ( икс равно пи на шесть плюс пи ка).
Ответ: х = + πk.
Построим график функции у = сtg x.
Рассмотрим два способа построения.
Первый способ аналогичен построению графика функции у = tg x.
Так как эта функция периодическая, состоит из бесконечного множества ветвей (в полосе между х = 0 и х =π , а также в полосе между х =π и х = 2π и т.д.) и нечетная, то построим по точкам часть графика на промежутке от нуля до пи на два (), затем воспользуемся симметрией и периодичностью.
Воспользуемся таблицей значений котангенса для построения графика.
Отметив полученные точки на координатной плоскости и соединим их плавной линией.
Так как график функции симметричен относительно , то построим такую же ветвь симметрично .
Применим периодичность, получим график функции у = сtg x.
Мы построили ветвь графика функции у = сtg x в полосе от х = 0 и х =π. Строим остальные ветви путем сдвига построенной ветви по оси x на π, – π, 2π, – 2π и так далее.
Второй способ построения графика функции у =сtg x.
Получить график функции у =сtg x проще всего с помощью преобразования тангенсоиды, используя формулу приведения ( котангенс икс равно минус тангенс от суммы икс и пи на два).
При этом сначала, сдвинем ветвь графика функции у =tg x вдоль оси абсцисс на вправо, получим
у = tg (x+ ), а затем выполняем симметрию полученного графика относительно оси абсцисс. В результате получится ветвь графика функции у =сtg x (рис.4). Зная одну ветвь, можем построить весь график используя периодичность функции. Строим остальные ветви путем сдвига построенной ветви по оси x на π, 2π, и так далее.
График функции у =сtg x называется тоже тангенсоида, как и график функции у =tg x. Ветвь, которая заключена в промежутке от нуля до пи, называют главной ветвью графика функции у =сtg x.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 37175 |
| Номер материала | 852 |