
Урок "Функции y = tgx, y = ctgx, их свойства и графики ч.2"

Краткое описание документа:
В данном видеоуроке дается подробный разбор, как решаются тригонометрические уравнения.
Вначале говорится о том, что на данном этапе обучения учащиеся уже знакомы некоторыми решениями тригонометрических уравнений. Ранее рассматривались уравнения sin t = a, cost = aдля значений а = 0; ±1; ±1/2 и некоторых других значений; ±. Эти уравнения не имеют решения, если модуль а больше единицы. Также были рассмотрены уравнения tg t =aи ctg t =a.
Как решаются уравнения данных видов? Автор приводит пример – решить уравнение cos t = - ½. Для решения используется числовая окружность на координатной плоскости. На окружности находим точки с координатой х =- ½, они соответствуют следующим числам t (используем таблицу значений): 2π/3 + 2πkи – 2π/3 + 2πk.
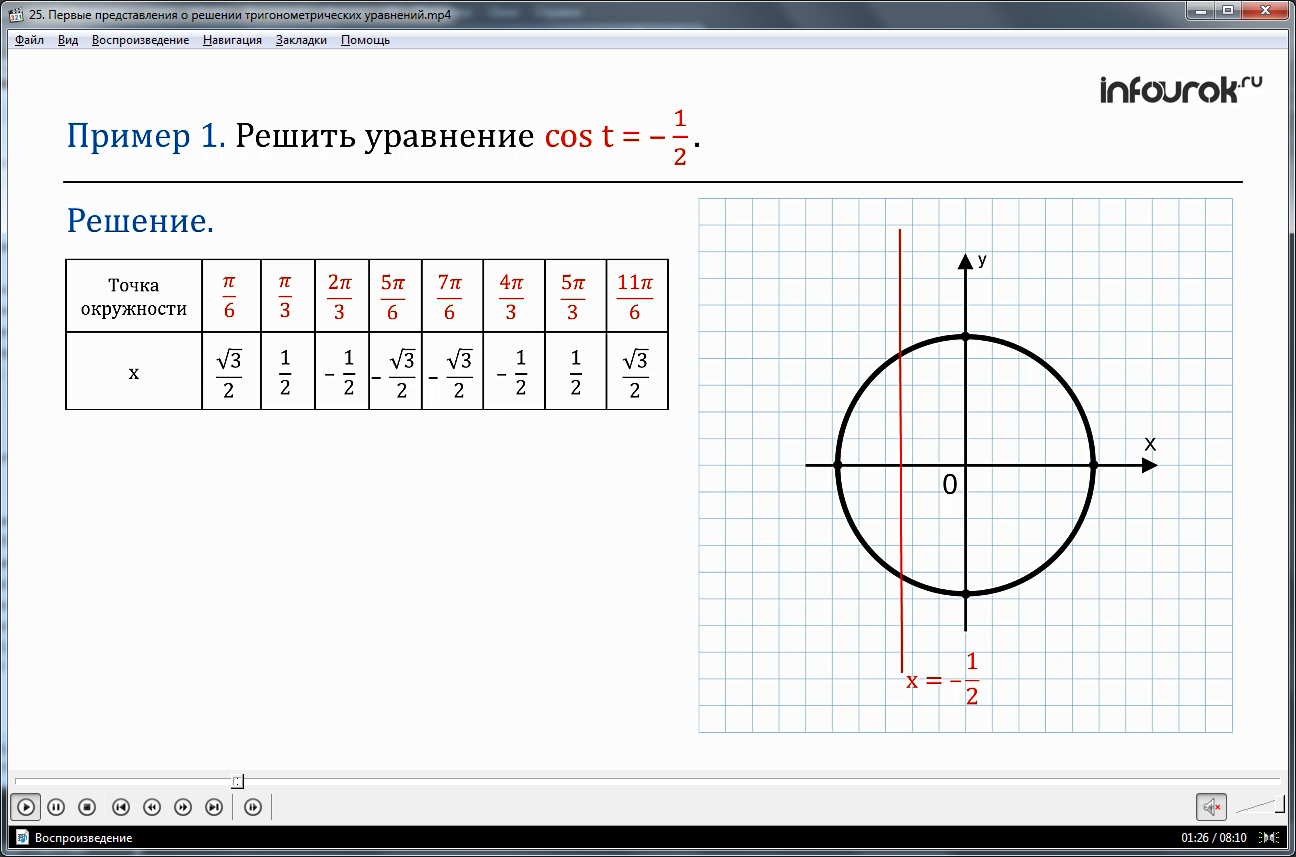
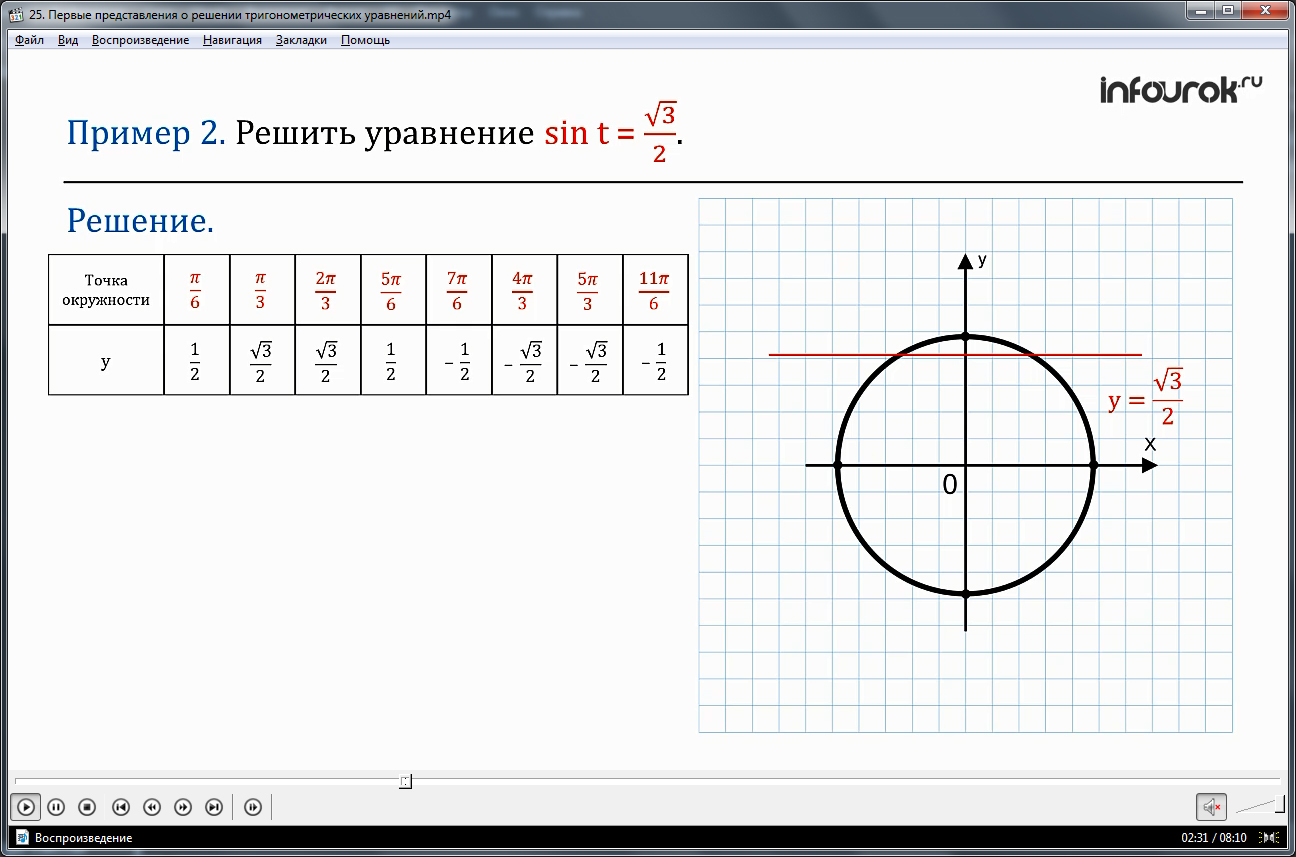
Далее рассматривается второй пример c sin t. Снова используем числовую окружность на координатной плоскости. Используя таблицу значений, найдем на окружности точки с координатой у, которые соответствуют значениям t: π/3 + 2πkи 2π/3 + 2πk.
Третий пример более сложный, чем два предыдущие.
Необходимо решить уравнение 2sin2t + sint – 1 = 0.
Решить данное уравнение можно путем замены переменных, в этом случае введем переменную z = sint. Путем алгебраических преобразований, используя дискриминант D = b2 – 4ac, находим, что z1 = – 1и z2 =1/2. Следовательно, sin t = – 1и sin t =1/2. Решаются эти уравнения путем нахождения соответствующих координат точек на окружности, используется таблица значений. Корнями уравнения являются t, равные – π/2 + 2πk; π/6 + 2πk; 5π/6+ 2πk.
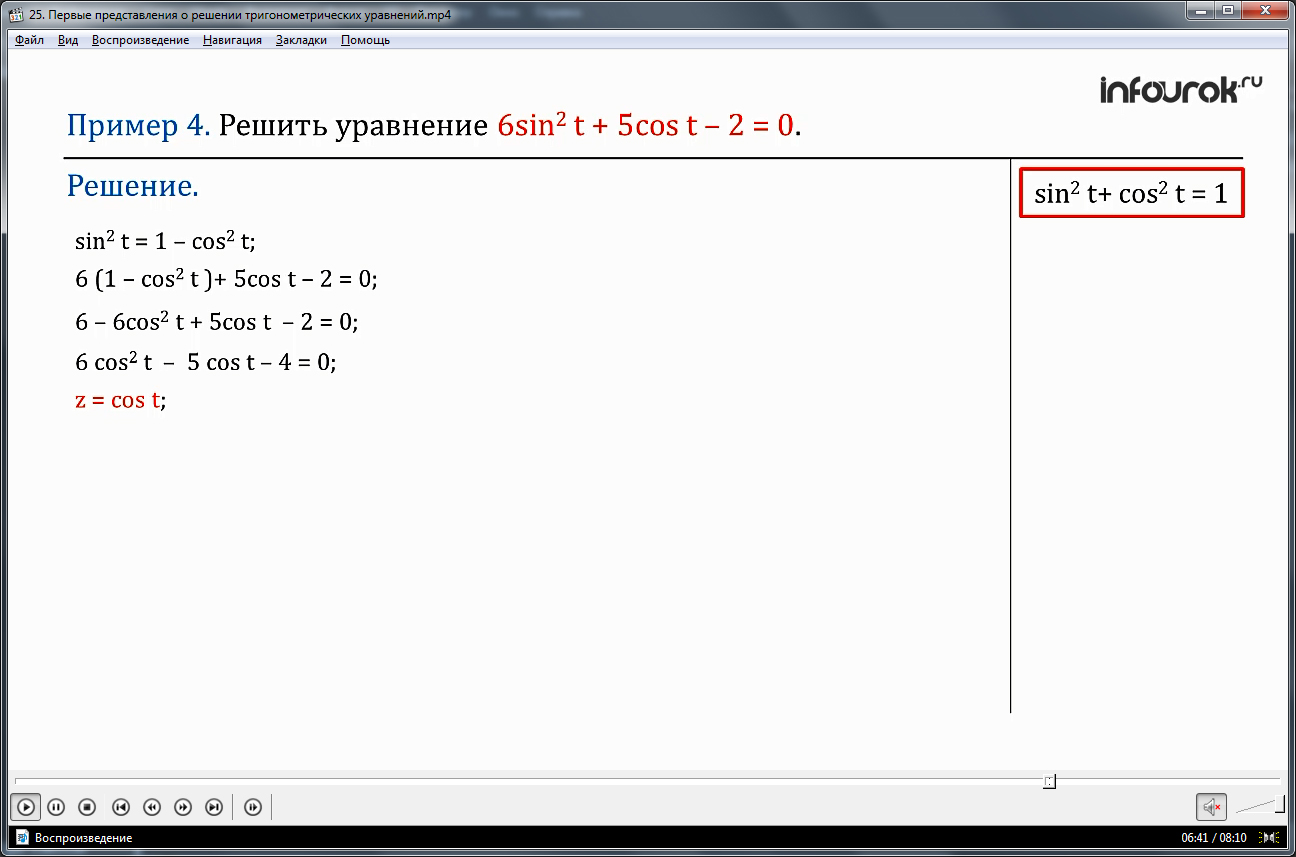
Разберем четвертый пример, решить уравнение 6sin2t + 5cos t – 2 = 0.
Используя формулу sin2 t + cos2 t = 0, исходное уравнение приведем к виду 6cos2t + 5cos t – 4 = 0.
Затем, как в предыдущем примере, после ввода новой переменной z = cos t и используя формулу дискриминанта, находим, что z1 = 4/3 и z2 = - 1/2. Т.е. cos t = 4/3 и cos t = - 1/2. Первое уравнение не имеет решений, т.к. 4/3 больше единицы (что также видно на единичной окружности); корень второго уравнения t = ± 2π/3 + 2πk. Решением уравнения 6sin2t + 5cos t – 2 = 0 будет t = ± 2π/3 + 2πk.
Практически вся информация, данная в уроке, это примеры решения тригонометрических уравнений различной степени сложности – от простых до более сложных. Решения задач подробно и последовательно разобраны. Поэтому изучение темы не вызовет трудностей у учащихся как на уроке, так и при самостоятельном ознакомлении. Современная и наглядная подача информации, такая, как видеоурок, позволит учителю эффективно использовать учебное время.
ТЕКСТОВАЯ РАСШИФРОВКА:
Мы уже научились решать тригонометрические уравнения вида sin t = a
( синус тэ равен а), cos t = a ( косинус тэ равен а), но только для следующих значений а : 0, 1, , , ( ноль, плюс минус один, плюс минус одна вторая, плюс минус корень из двух на два, плюс минус корень из трех на два). Эти уравнения не имеют решений при | а | 1( модуль а больше единицы). Уравнения же вида tg t = a ( тангенс тэ равен а) и ctg t = a ( котангенс тэ равен а) тоже мы пока решаем для конкретных значений а: 0, 1, , ( ноль, плюс минус один, плюс минус корень из трех на три, плюс минус корень из трех).
Вспомним, как решаются уравнения данного вида.
ПРИМЕР 1. Решить уравнение cos t = - ( косинус тэ равен минус одна вторая).
Решение. Будем использовать числовую окружность на координатной плоскости.
ПРИМЕР 2. Решить уравнение sin t = ( синус тэ равно корень из трех, деленное на два).
Решение. Будем использовать числовую окружность на координатной плоскости.
Рассмотрим решение некоторых более сложных уравнений.
ПРИМЕР 3. Решить уравнение 2 sin2t + sint – 1 = 0.(два синус квадрат тэ плюс синус тэ минус один равно нулю)
Решение. Данные уравнения решаются методом замены переменной.
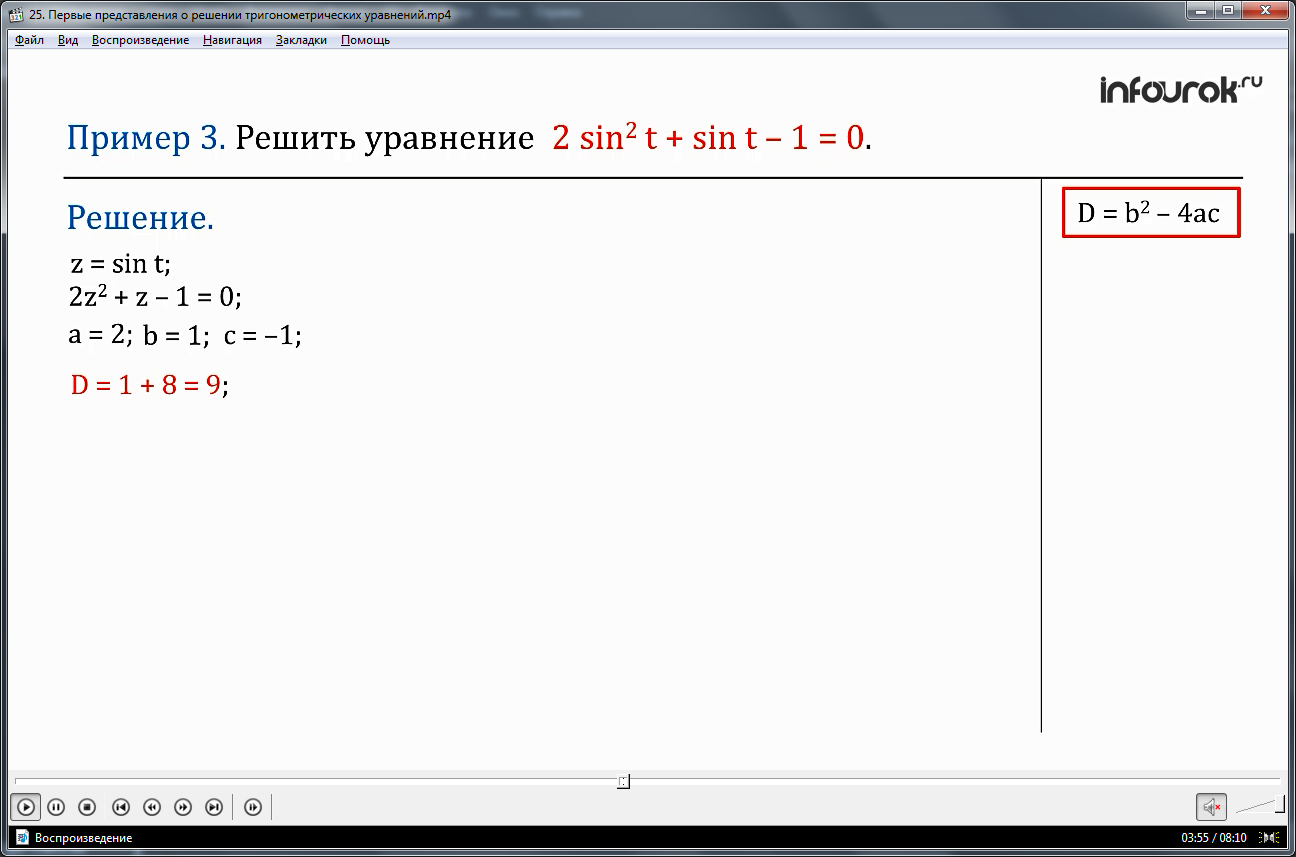
Введем новую переменную z = sint ( зэт равно синус тэ). Тогда данное уравнение примет вид: 2 z2 + z – 1 = 0 ( два зэт квадрат плюс зэт минус один равно нулю). Мы получили квадратное уравнение, которое будем решать, используя дискриминант: D = b2 – 4 ac( дэ равно бэ квадрат минус четыре а цэ). В нашем случае, a = 2, b = 1, c = - 1.Значит, D = 1 + 8 = 9. Для нахождения корней квадратного уравнения воспользуемся формулой:
z = (зэт равно минус бэ плюс минус корень из дэ, деленное на два а).
Получим z1 = - 1( зэт один равно минус один), а z2 = ( зэт два равно одной второй). Значит, sint = –1 или sint =.
1) sint = –1, ордината точки равна минус одному при t=– , на окружности это точка D, и значит данное уравнение соответствует любому t равному t=– +2πk, kZ
2) найдем на числовой окружности точки с ординатой . (показать таблицу)
На числовой окружности точка R (эр) соответствует числу , а значит, и любому числу вида + 2πk ( пи на шесть плюс два пи ка). Точка S(эс) соответствует числу , а значит, любому числу вида + 2πk ( пять пи на шесть плюс два пи ка). kZ
ПРИМЕР 4.Решить уравнение 6 sin2t + 5 cos t – 2 = 0( шесть синус квадрат тэ плюс пять косинус тэ минус два равно нулю).
Решение. Вспомним основное тригонометрическое тождество: sin2t+ cos2 t = 1. Из данного тождества выразим sin2t, sin2t = 1 – cos2 t ( синус квадрат равен разности единицы и квадрата косинуса тэ). Заменим sin2t в уравнении полученным выражением, 1 – cos2 t , получим квадратное уравнение относительно cos t:
6( 1 – cos2 t )+ 5 cos t – 2 = 0
Раскроем скобки 6 – 6cos2 t + 5 cos t – 2 = 0
Приведем подобные слагаемые получим:
6 – 6cos2 t + 5 cos t + 4 = 0
6 cos2 t - 5 cos t – 4 = 0
( шесть косинус квадрат тэ минус пять косинус тэ минус четыре равно нулю).
Введем новую переменную z = cos t ( зэт равно косинус тэ). Тогда данное уравнение примет вид: 6 z2 - 5z – 4 = 0. Дискриминант этого квадратного уравнения равен D = b2 – 4 ac, где а= 6, b= -5, с= -4 Подставляем данные в формулу дискриминанта и получаем ( - 5)2 – 4 ∙ 6 ∙ ( - 4) = 25 + 96 =121( дэ равно двадцать пять плюс девяноста шесть равно сто двадцать один).
Значит, cos t = , либо cos t =.
Первое из этих уравнений не имеет решений, так как 1( четыре трети больше единицы), так как если мы вспомним график функции у=cosx то его множество значений Е(f)=[–1;1], или же обратимся к единичной окружности
на которой четко видно сто косинус определен от –1 до 1. (–1 cos t 1)
Решая второе уравнение (обратимся к решению примера 1), находим t = ± + 2πk( тэ равно плюс минус два пи на три плюс два пи ка).
Ответ:t = ± + 2πk.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4098 |
| Номер материала | 853 |