
Урок «Функция у=log_а%U2061х,ее свойства и график»

Краткое описание документа:
Повторим определение логарифма: (логарифм — это показатель степени, в которую нужно возвести основание, что бы получить подлогарифмическое выражение).
Рассмотрим одновременно две функции: показательную - и логарифмическую – у= .
Если точка (m;n) (рис.1) принадлежит графику показательной функции – то выполняется равенство . Запишем это равенство, используя определение логарифма m=(эм равно логарифму числа эн по основанию а). Из этого равенства следует, что точка (n;m) принадлежит графику логарифмической функции у=. Ранее при изучении функции у= (игрек равно корень энной степени из икс) была доказана теорема о симметричности точек (m;n) и (n;m) относительно прямой (игрек равняется икс) у=х, значит, справедливо утверждение:
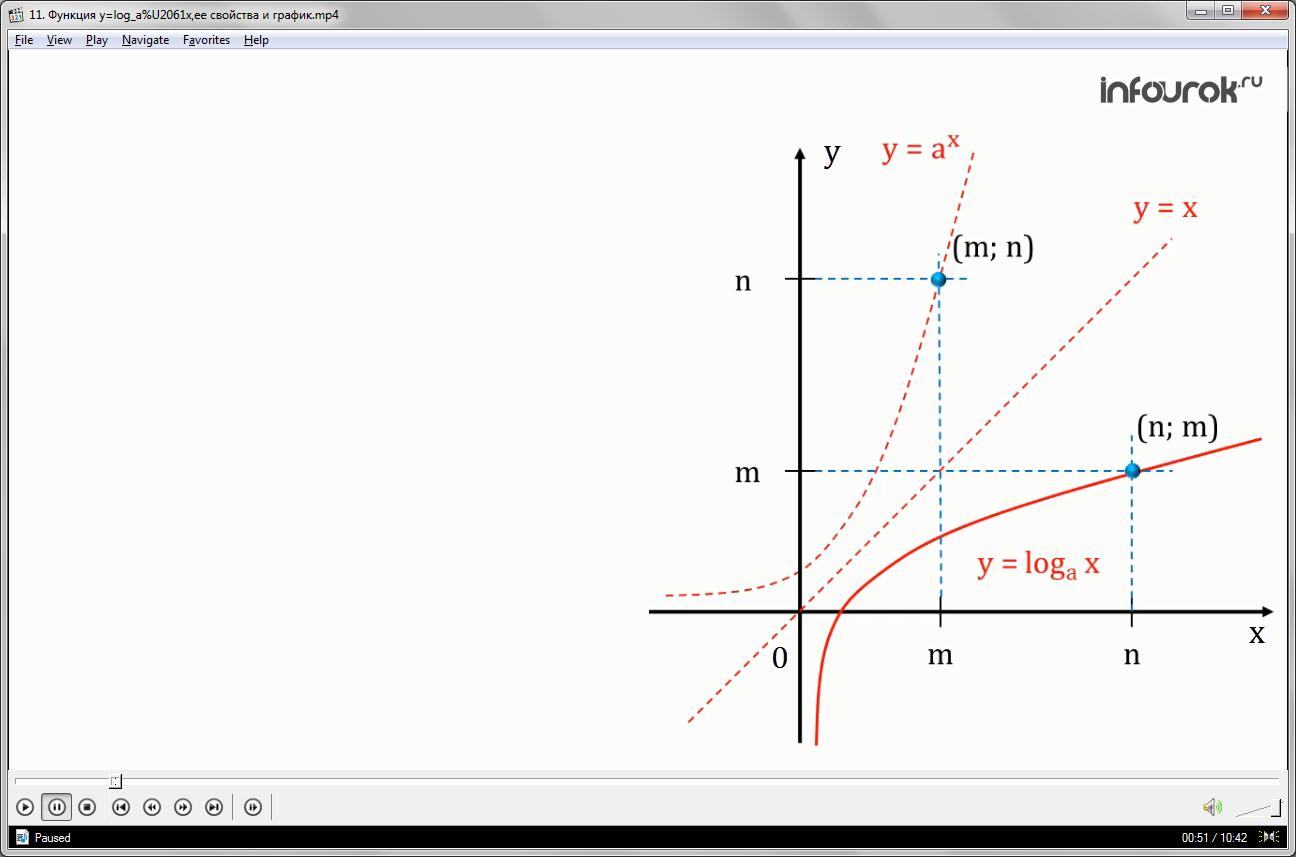
График логарифмической функции у=
симметричен графику показательной функции относительно прямой у=х (игрек равен икс)
Изобразим схематически графики логарифмической и показательной функций при
и при (при а меньшем единицы, но большем нуля):
График логарифмической функции называют логарифмической кривой.
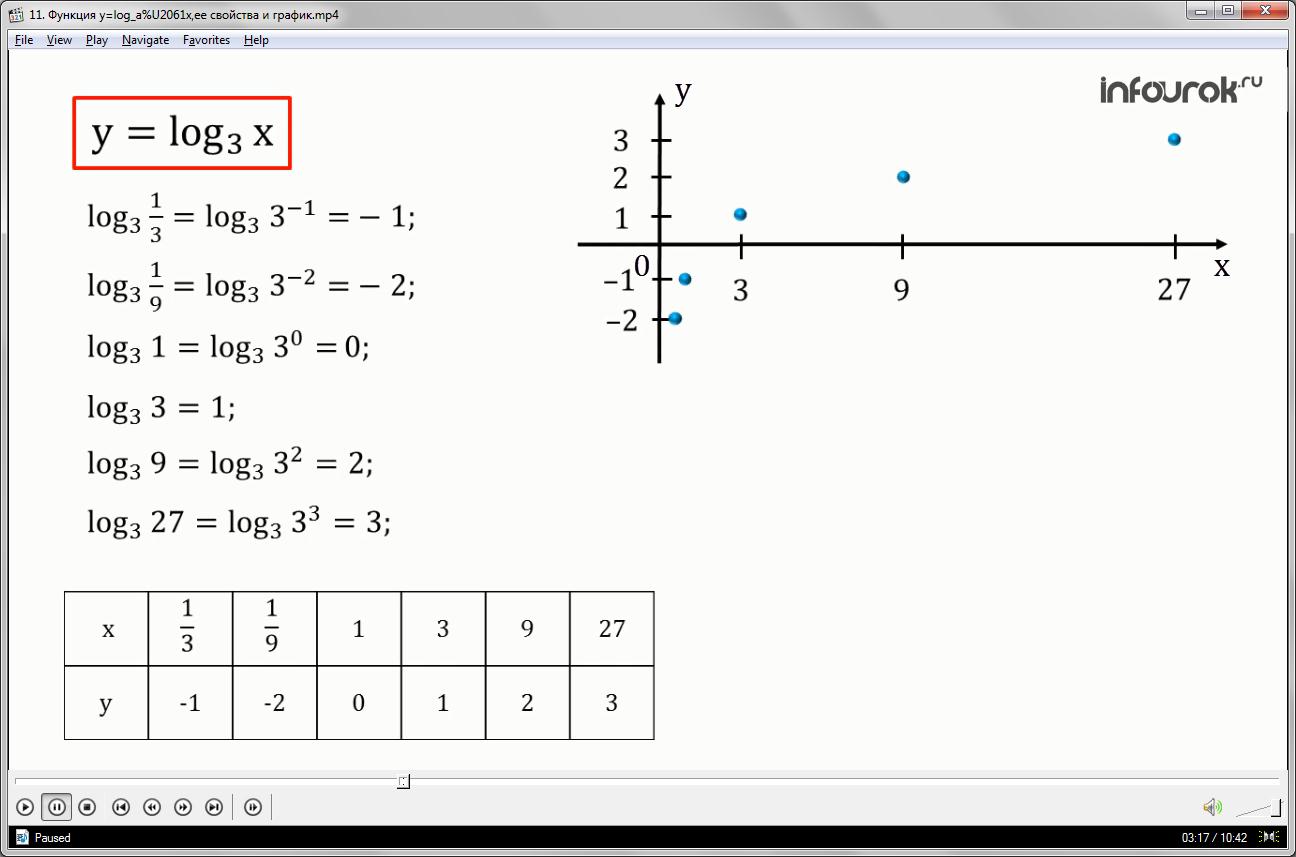
Построим график логарифмической функции с основанием три
(логарифм это показатель степени, в которую нужно возвести основание, что бы получить подлогарифмическое выражение), т.е..
|
х |
1 |
3 |
9 |
27 |
||
|
у |
-1 |
-2 |
0 |
1 |
2 |
3 |
Отметив на координатной плоскости точки из таблицы, проведем через них логарифмическую кривую. (Рис.2)
Используя построенный график, укажем свойства логарифмических функций с основанием большим единицы
- D(f)=область определения — интервал от нуля до плюс бесконечности)
- E(f)=область значения – множество всех действительных чисел
- Функция не является ни четной, ни нечетной.
- Возрастает на на всей области определения)
- Не ограничена сверху, не ограничена снизу.
- Не имеет ни наибольшего, ни наименьшего значений.
- Непрерывна.
- Выпукла вверх.
Построим график функции у=
|
х |
9 |
3 |
1 |
||
|
у |
-2 |
-1 |
0 |
1 |
2 |
(рис.3)
Используя построенный график, укажем свойства логарифмических функций с основанием меньшим единицы, но большим нуля
- D(f)=область определения — интервал от нуля до плюс бесконечности).
- E(f)=область значения – множество всех действительных чисел.
- Не является ни четной, ни нечетной.
- Убывает на на всей области определения)
- Не ограничена сверху, не ограничена снизу.
- Не имеет ни наибольшего, ни наименьшего значений.
- Непрерывна.
- Выпукла вниз.
Заметим, что ось ординат является вертикальной асимптотой графика логарифмической функции с любым допустимым основанием.
Пример 1: Найдите наибольшее и наименьшее значения функции на заданном промежутке: (икс принадлежит отрезку от одной третьей до девяти).
Так как основание логарифмической функции больше единицы, то данная функция непрерывна и возрастает на всей области определения, следовательно, и на указанном интервале. Значит, наибольшее и наименьшее значения она принимает на концах заданного отрезка. Найдем : для этого вместо икса подставим и используем формулу, которую мы выделили при изучении понятия логарифма:
(логарифм числа а в степени эм по основанию а равен эм) получим
Подставив вместо икса 9, найдем
Пример 2: Решите неравенство
Рассмотрим функции у=.
1)Чтобы найти абсциссу точки пересечения их графиков, решим уравнение
2) Построим график функции у= (рис.4)
Таблица для графика у=
|
х |
1 |
2 |
4 |
||
|
у |
-2 |
-1 |
0 |
1 |
2 |
График функции (игрек равен логарифм числа икс по основанию два) расположен ниже прямой у=1 при икс меньшем двух.
3) Запишем ответ
Пример 3: решите неравенство
В одной системе координат построим графики функций
(игрек равен логарифм числа икс по основанию два и игрек равен минус икс плюс один) (рис.5)
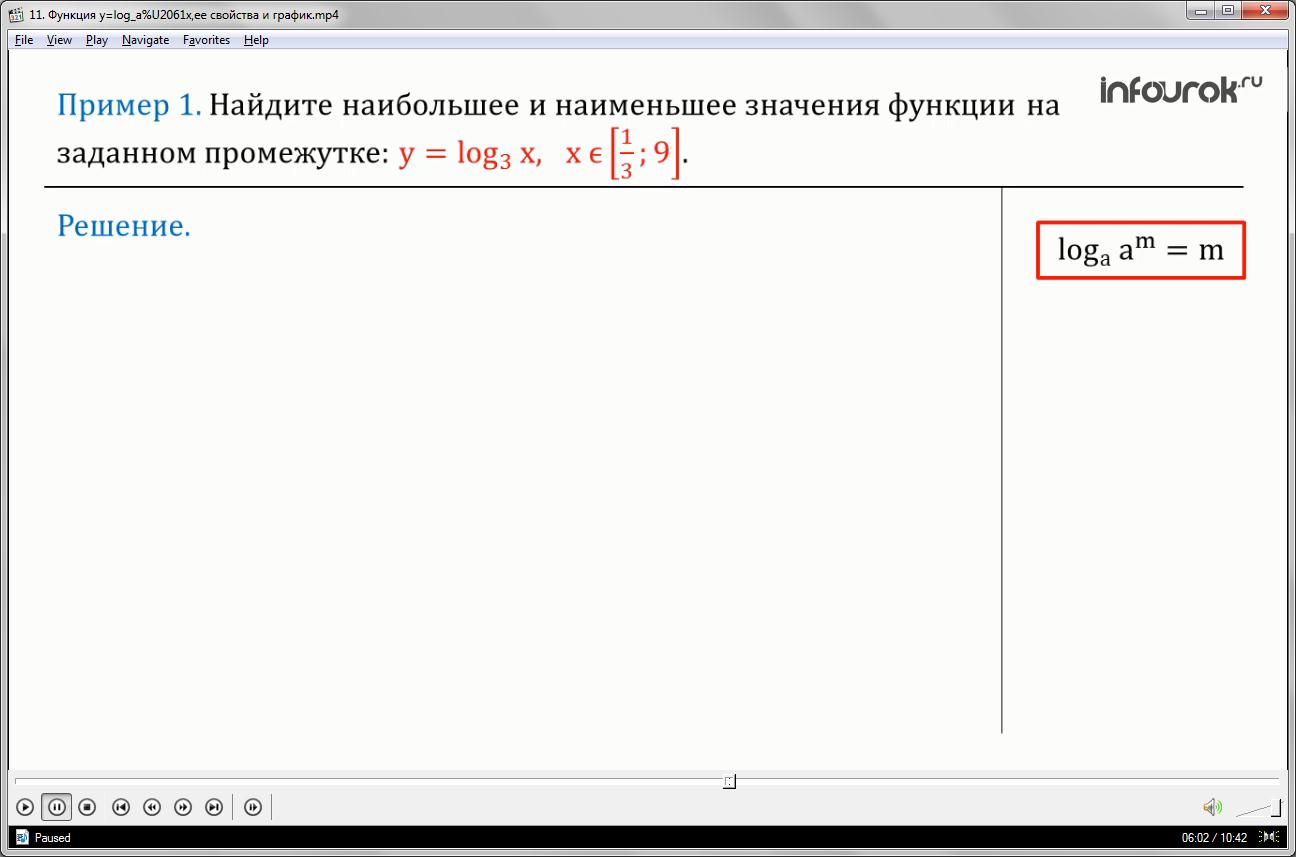
Таблица для графика у=
|
х |
1 |
2 |
4 |
||
|
у |
-2 |
-1 |
0 |
1 |
2 |
Графиком функции является прямая, которая проходит через точки (0;1) и (1;0).
Мы видим, что график функции у= расположен выше графика функции , при икс большем либо равном единице.
Ответ
Пример 4: Постройте график функции
Построим вспомогательную систему координат, для этого ось абсцисс перенесем вправо на четыре единичных отрезка, т.е. построим прямую х′=4, а
ось ординат поднимем на два единичных отрезка вверх, т.е. построим прямую у′=2. В новой системе построим график функции у=
(рис.6)
Таблица для графика у=
|
х |
1 |
3 |
9 |
||
|
у |
-2 |
-1 |
0 |
1 |
2 |
Пример 5: построить график функции и указать его свойства
У=
Построим график функции у= при (игрек равен три в степени икс, при икс больше единицы)
|
х |
2 |
3 |
4 |
|
у |
9 |
27 |
81 |
В этой же системе координат построим график функции и
у= (игрек равен логарифм числа икс по основанию одна третья, при икс меньшем либо равном единице)
|
х |
1 |
|||
|
у |
3 |
2 |
1 |
0 |
Рис. 7
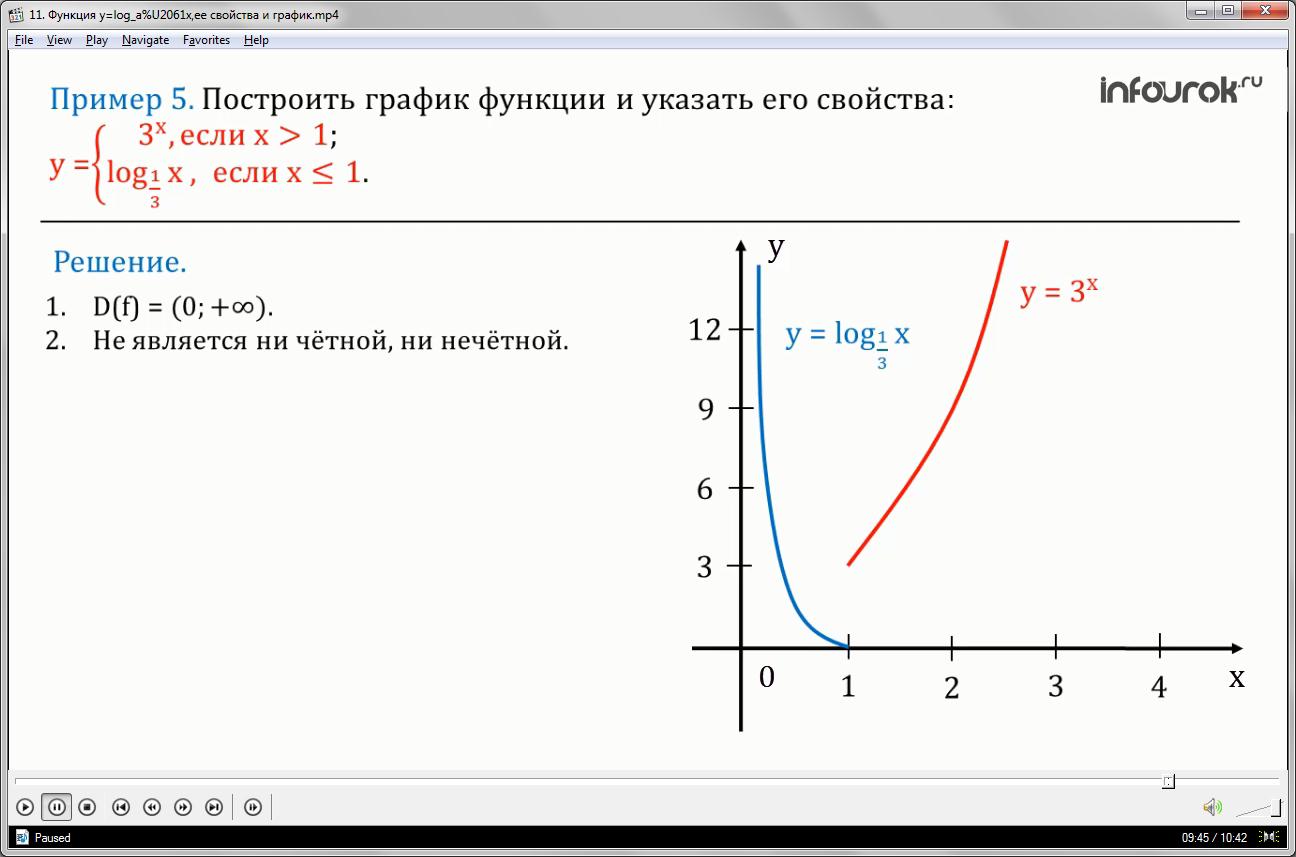
Укажем свойства данной функции:
- D(f)= (область определения интервал от нуля до плюс бесконечности).
- Не является ни четной, ни нечетной.
- Убывает на интервале (от нуля до единицы включительно), возрастает на интервале (1;+ (от единицы до плюс бесконечности).
- Не ограничена сверху, ограничена снизу.
- Наибольшего значения не принимает, наименьшее значение
(равно нулю при икс равном единице)
- Функция претерпевает разрыв в точке х=1, а в остальных точках она непрерывна.
- E(f)= (область значения — луч от нуля до плюс бесконечности).
Выпукла вниз на промежутках
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6038 |
| Номер материала | 1060 |