
Урок «Функция вида у=v(n&x), их свойства и график»

Краткое описание документа:
Рассмотрим функцию у= (игрек равняется корень энной степени из икс) при условии (значение аргумента неотрицательно).
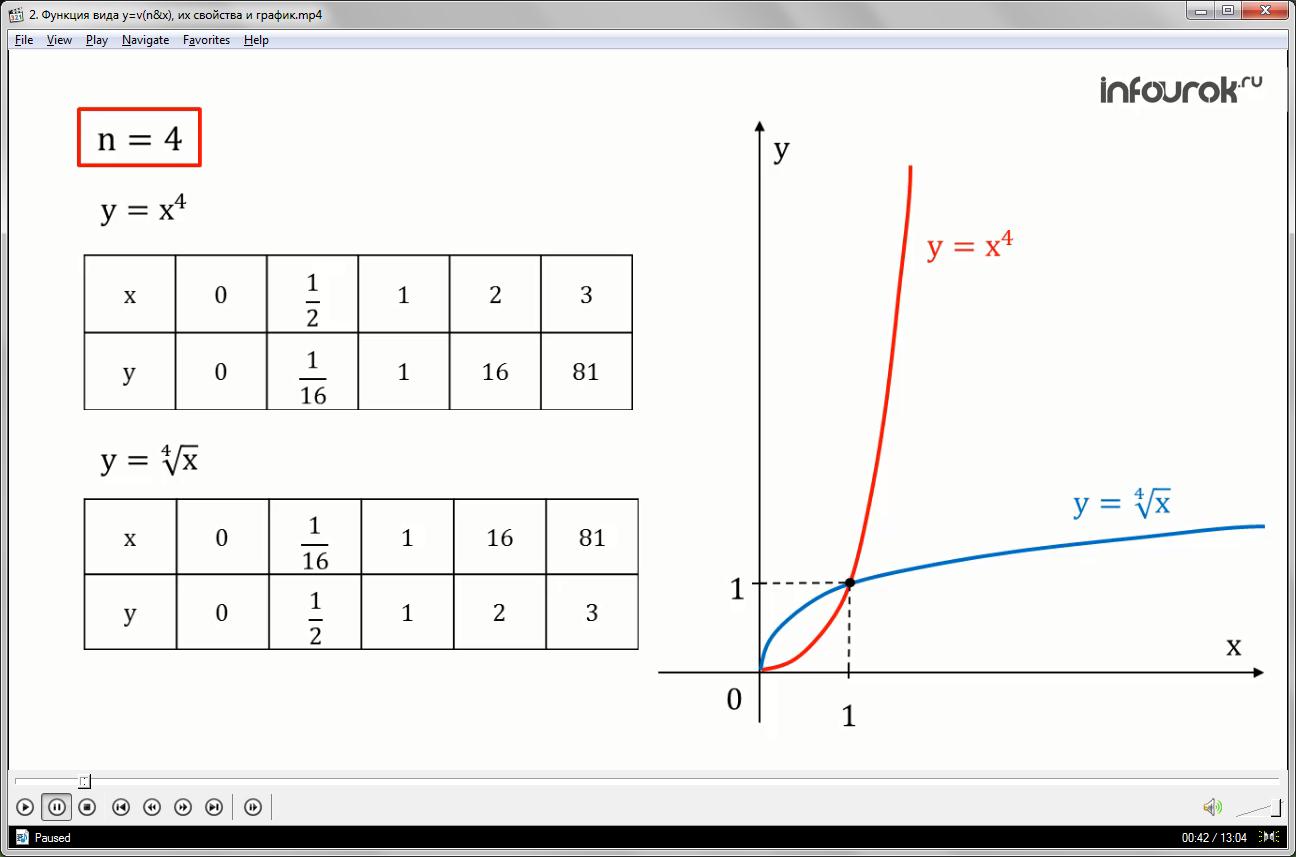
Пусть n=4. Построим в одной системе координат два графика функций (игрек равняется икс в четвертой степени и игрек равняется корень четвертой степени из икс)
Рис.5
|
х |
0 |
2 |
3 |
|
у |
0 |
16 |
81 |
|
х |
0 |
16 |
81 |
|
у |
0 |
2 |
3 |
Внимательно рассмотрев графики и таблицы, можно заметить, что графики представляют собой ветвь параболы и симметричны относительно прямой у=х (игрек равен икс), так как на построенных ветвях парабол есть точки, которые симметричны друг другу относительно данной прямой. Так точка А графика функции с координатами (
. Если рассмотреть точки с координатами (2;16) и (16;2), (3;81) и (81;3), то заметим, что они также симметричны относительно прямой х=у. А точки с координатами (0;0) и (1;1) лежат на данной прямой и являются общими для парабол.
Значит, для любой точки (m;) на графике есть ей симметричная точка (на графике относительно прямой у=х, справедливо будет и обратное утверждение.
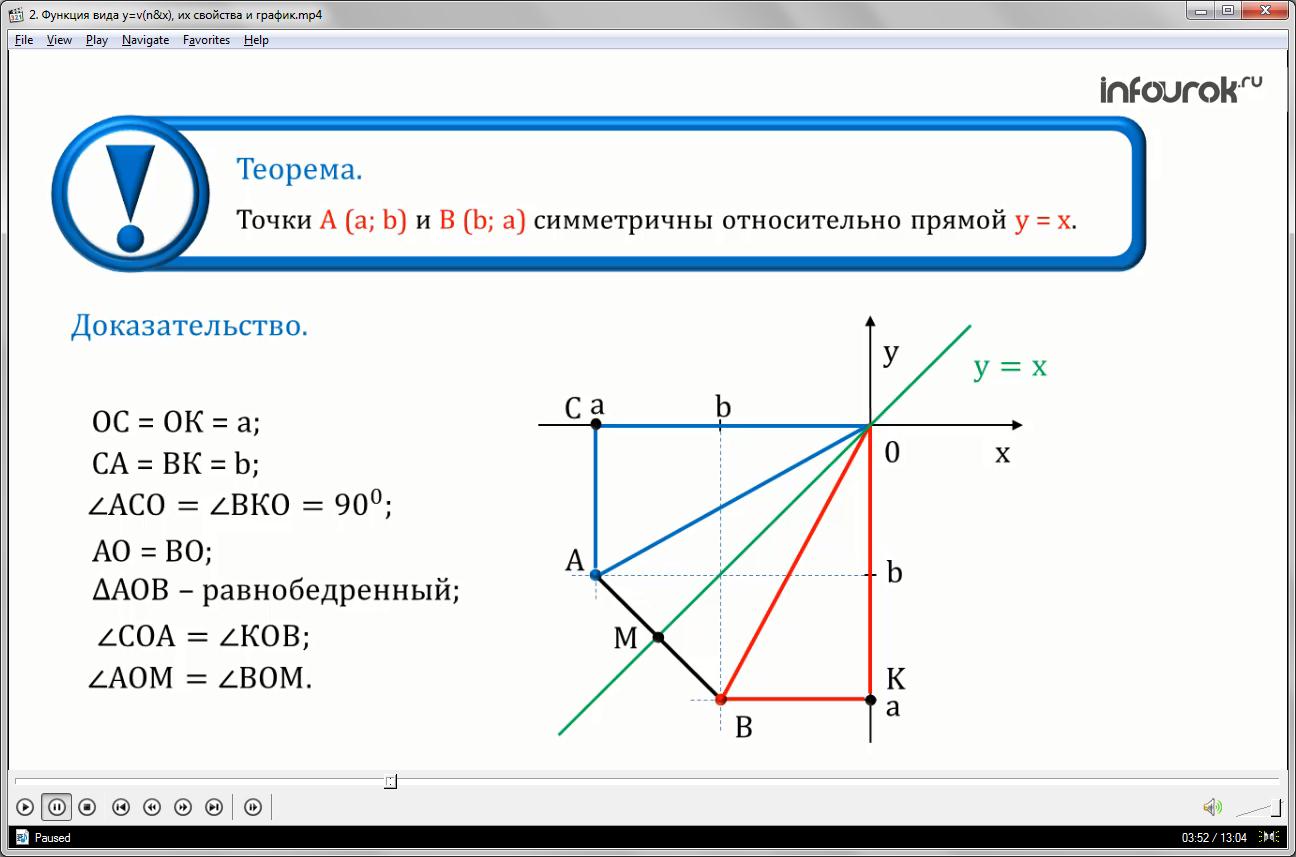
Докажем следующую теорему:
Точки А (a;b) и В (b;a) симметричны относительно прямой у=х.
Доказательство: предположим, что a и b – отрицательные числа. Значит, точки А (a;b) и В (b;a) расположены в третьей координатной четверти. А прямая у=х является биссектрисой первой и третьей координатных четвертей. На оси абсцисс отметим точку С (а;0), а на оси ординат точку
К(0; а) (рис.6).
Рассмотрим треугольники СОА и КОВ: ОС=ОК=а по построению,
СА=ВК= b по построению, , следовательно треугольники равны по первому признаку равенства треугольников. Значит, 1)АО=ВО и следавательно треугольник АОВ — равнобедренный.
2) , и так как прямая у=х является биссектрисой угла СОК по построению, то и и ОМ является биссектрисой треугольника АОВ, а следовательно и осью симметрии для точек А и В. Аналогично проводится доказательство и при условии если a и b – положительны.
Сделаем вывод: график функции (игрек равняется корень кубический из икса) можно получить из графика функции ( игрек равняется икс в третьей степени), при х, с помощью преобразования симметрии относительно графика прямой у=х (игрек равняется икс). Таким же образом можно построить график функции у= (игрек равняется корень шестой степени из икса) при (положительном икс) с помощью преобразования симметрии графика функции у= (игрек равняется икс в шестой степени), при (положительном икс), относительно прямой у=х (игрек равняется икс). (рис.6а)
Обобщим полученные результаты: график функции (игрек равен корень энной степени из икс), при х и n – нечетное,симметричен относительно прямой у=х графику функции у=(игрек равен икс в энной степени)(рис.7)
Сформулируем свойства функции
(игрек равняется корень энной степени из икса, с нечетной степенью при икс меньшим либо равным нулю)Рис.8
- D(f)= (областью определения функции является интервал от минус бесконечности до нуля)
- (областью значений функции является интервал от минус бесконечности до нуля)
- Функция не является ни четной, ни нечетной.
- Возрастает на луче (от минус бесконечности до нуля)
- Ограничена сверху, не ограничена снизу.
- (максимальное значение функции равно нулю), наименьшего значения не имеет.
- .
Для того чтобы записать восьмое свойство в этой системе координат, построим график функции у= (игрек равняется икс в третьей степени, при икс меньшем либо равном нулю). Мы можем видеть, что все свойства функции ( игрек равняется корень третьей степени из икса, при икс меньшем либо равном нулю) и построенной полностью совпадают, несмотря на то, что функции различны. Для того чтобы функции различать, были введены понятия выпуклости вверх – у= и выпуклости вниз – у= (рис.9). Как это определить? Достаточно соединить отрезком любые две точки графика, и если график функции расположен выше построенного отрезка, то функция выпукла вверх, а если график функции расположен ниже построенного отрезка, то функция выпукла вниз.
Сформулируем восьмое свойство.
8. Функция выпукла вниз на луче (от минус бесконечности до нуля)
9. Функция дифференцируема в любой точке х
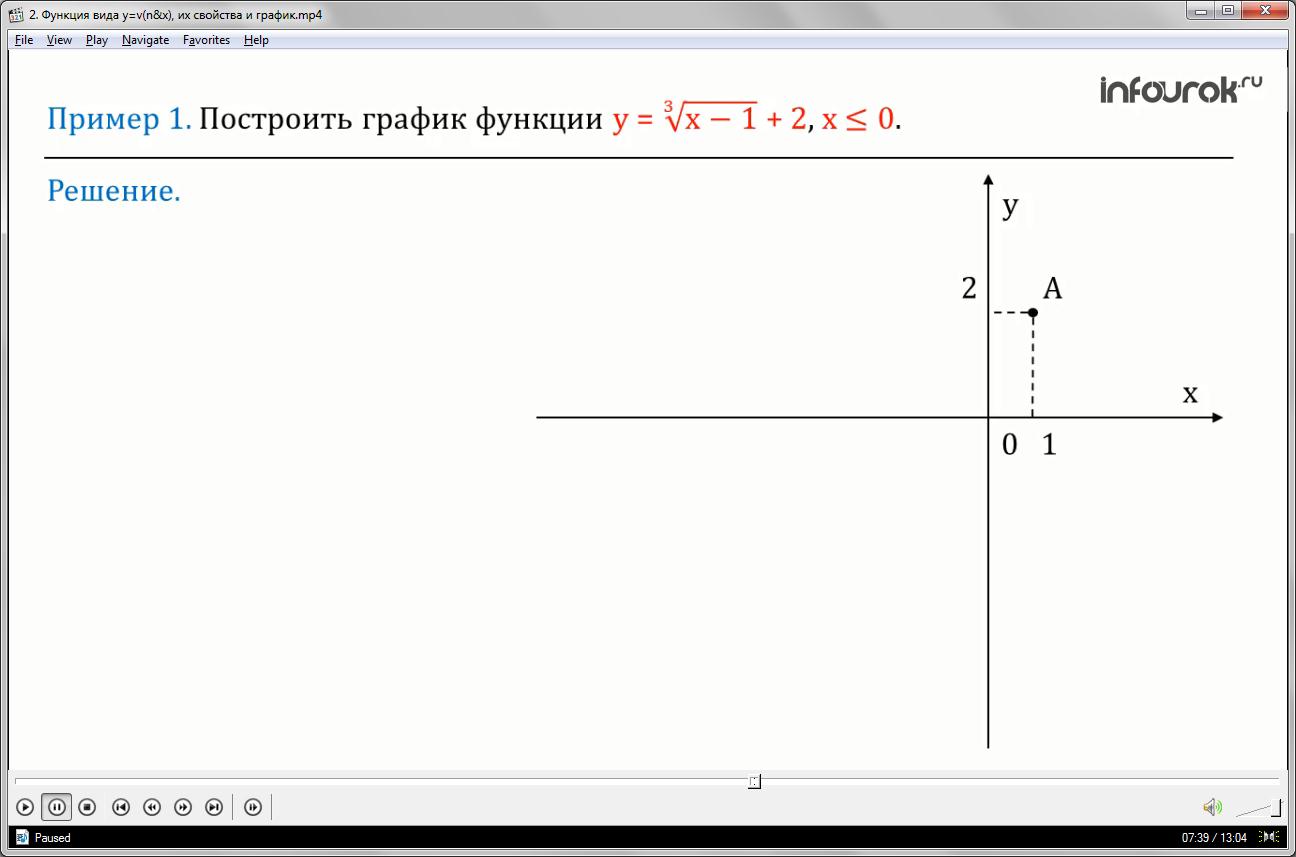
Пример 1: Построить график функции у=+2, х (рис. 10)(игрек равняется сумме корня третьей степени из икс минус один и двух)
Для построения данного графика функции нам нужна вспомогательная система координат с началом в точке А (1;2) – пунктирные прямые х′=1(икс штрих равен единице) и у′=2 (игрек штрих равен двум) на рис10. В новой системе координат построим график (игрек равен корень третьей степени из икса).
Таблица
|
х |
-8 |
-1 |
0 |
|
у |
-2 |
-1 |
0 |
Это и будет график данной функции.
Пример 2.
Решите уравнение (корень пятой степени из икса равен минус икс минус два)
В одной системе координат построим графики двух функций у= (игрек равняется корень пятой степени из икса)
|
х |
-32 |
-1 |
0 |
1 |
32 |
|
у |
-2 |
-1 |
0 |
1 |
2 |
и у=-х-2(игрек равняется минус икс минус два)( графиком является прямая, которую построим по двум точкам)
|
х |
-2 |
0 |
|
у |
0 |
-2 |
(рис.11) графики пересекаются в точке В (-1;-1) (с координатами минус один, минус один). Значит, абсцисса данной точки х= -1 и есть корень данного уравнения.
Пример 3: Построить и указать свойства функции у= .
Построим график функции у=(игрек равняется корень четвертой степени из икса, при икс больше либо равном единицы)(рис 13а)
|
х |
1 |
16 |
81 |
|
у |
1 |
2 |
3 |
Построим график функции у= , х (игрек равняется икс в третьей степени при икс меньшем либо равном единицы)(рис.13б)
|
х |
-2 |
-1 |
0 |
1 |
|
у |
-8 |
-1 |
0 |
1 |
В одной системе координат изобразим построенные части графиков и получим график данной функции (рис 13).
Используя построенный график (рис 13), запишем свойства данной функции:
- область определения - множество действительных чисел)
- возрастает на всей области определения
- не ограничена ни сверху, ни снизу
- функция не имеет наибольшего и наименьшего значений
- непрерывна
- E(f)=(область значений функции — есть множество действительных чисел)
- Выпукла вниз на отрезке (от нуля до единицы), выпукла вверх при хи на луче((от минус бесконечности до нуля)
- Функция дифференцирована везде
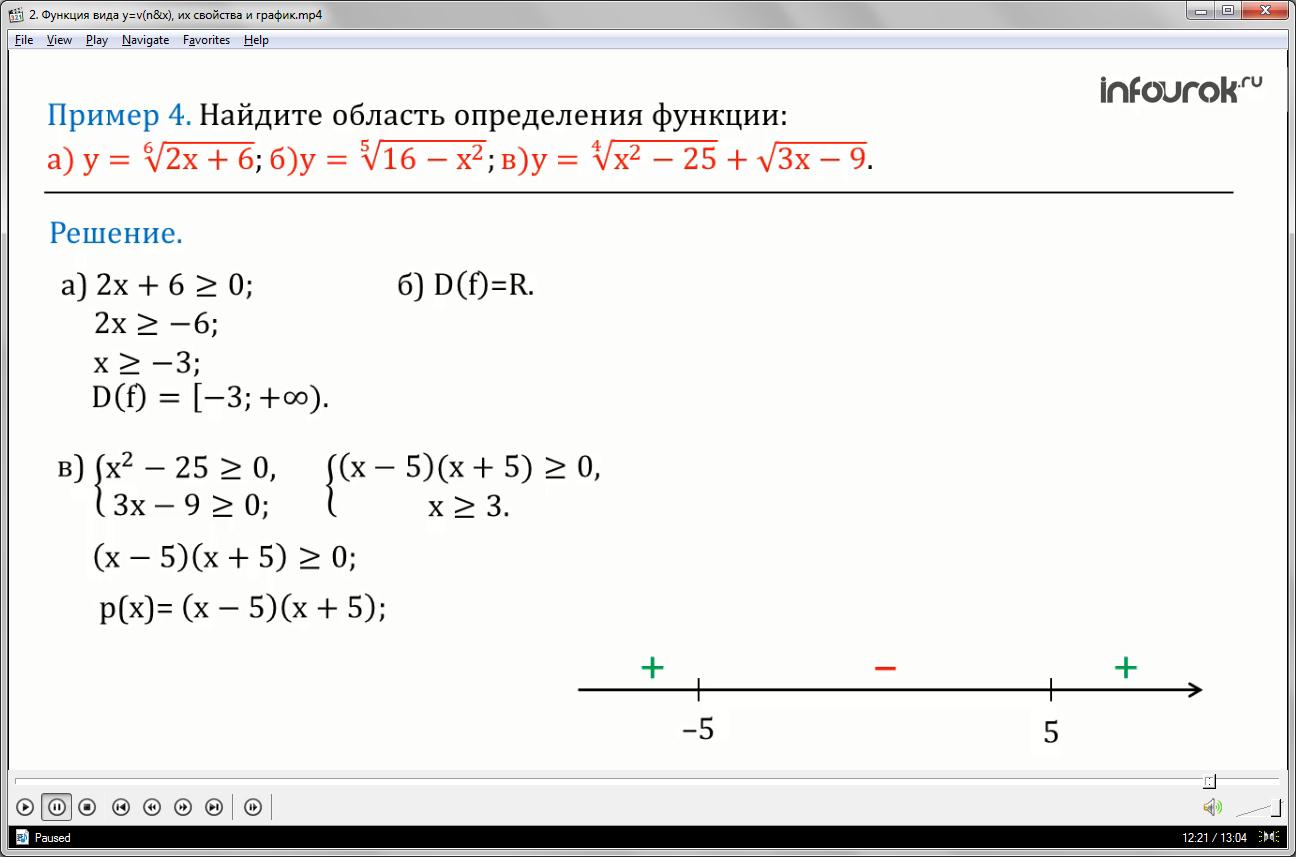
Пример 4: Найдите область определения функции
а) Так как корень четной степени, то под корнем может находиться только неотрицательное число, следовательно необходимо решить неравенство
Значит, (область определения данной функции — луч от минус трех до плюс бесконечности).
б) Так как корень нечетной степени, то под корнем может находиться любое число, следовательно, областью определения является множество действительных чисел =R.
в) Данная функция состоит из двух слагаемых четной степени, значит, нужно решить систему неравенств, где каждое из неравенств должно иметь смысл при каждом значении переменной икс.
Решим первое неравенство системы, для этого левую часть неравенства разложим на множители и получим. Левая часть полученного неравенства обращается в нуль в точках 5 и -5. Отметим эти точки на числовой прямой:
Числовая прямая разбивается указанными точками на три промежутка, на каждом из которых выражение р(х)= сохраняет постоянный знак (рис 14а). Промежуток, на котором выполняется неравенство р(х), заштрихован на рис.14а.
Для решения второго неравенства системы перенесем в правую часть 9 и разделим обе части неравенства на 3, получим
На одной координатной прямой отметим решение каждого неравенства, использовав для первого верхнюю штриховку, а для второго – нижнюю (рис. 14).
Промежуток, где штриховки совпали, и есть область определения данной функции. А именно (луч от пяти до плюс бесконечности)
Повторим еще раз, как изображаются графики функции
Если n — четное (рис. 15)
Если n — нечетное (рис.16)
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5064 |
| Номер материала | 1051 |