
Урок "Функция y=cosx, ее свойства и график"

Краткое описание документа:
Видеоурок «Функция у = cos х, ее свойства и график» представляет наглядный материал для изучения данной темы. В пособии представлены особенности функции, ее свойства, а также описания решения задач, в которых применяются знания о свойства косинуса. С помощью видеоурока учителю легче предоставить требуемые знания и сформировать умения учеников. Наглядное пособие может помочь повысить эффективность урока, обеспечив более глубокое понимание материала и лучшее запоминание, а также освободив время урока для проведения индивидуальной работы.
Использование видеоурока дает учителю преимущество для более эффективной подачи материала. Пособие может применяться только для наглядности, сопровождая объяснение учителя или в качестве самостоятельной части урока, давая возможность учителю улучшить индивидуальную работу с учениками. Демонстрируемые построения графиков, преобразования в помощью анимационных эффектов становятся более понятными для учеников, помогают освоить навыки решения задач с использованием данного материала. Выделение и озвучивание свойств функции инструментами видеоурока помогает лучше их запомнить.
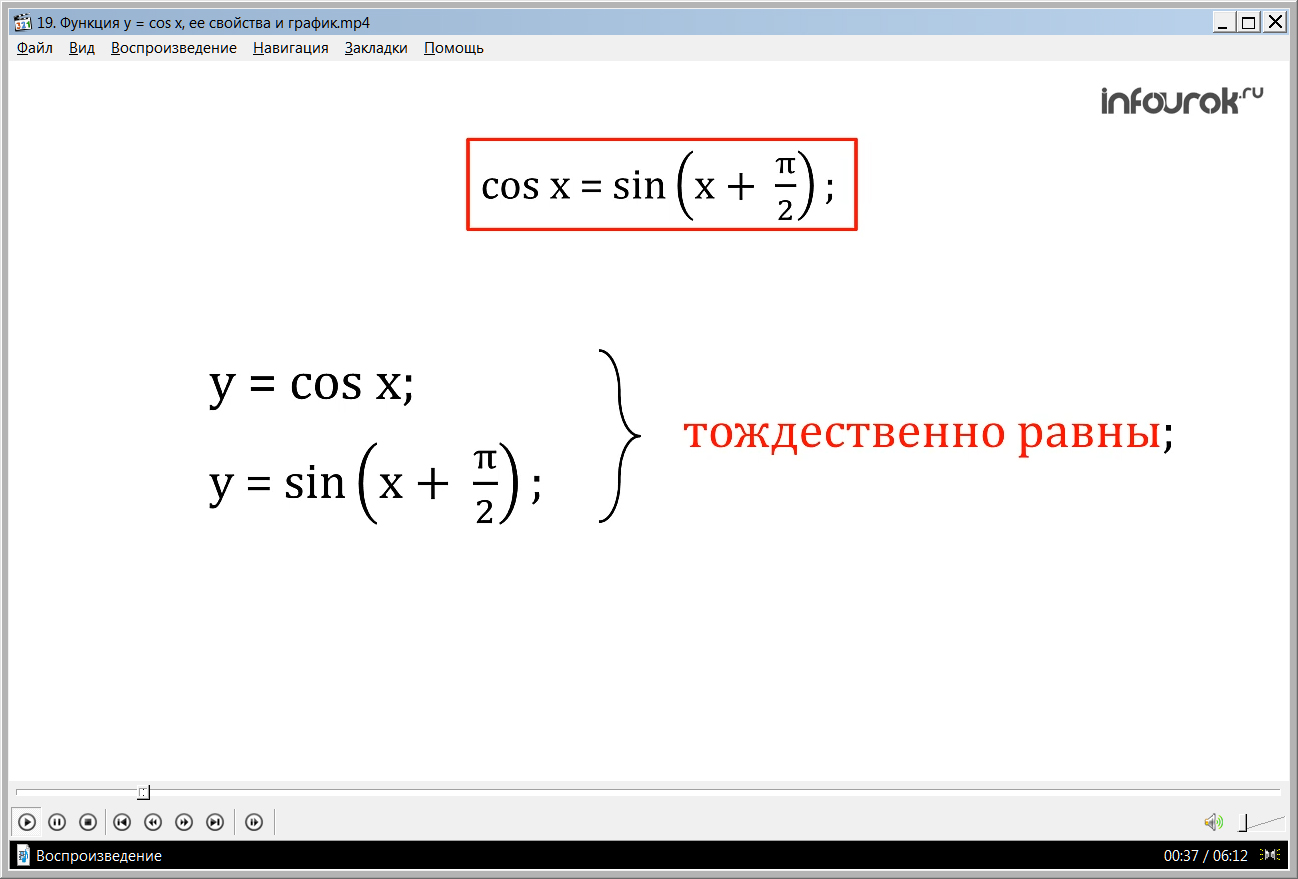
Демонстрация начинается с представления названия темы. Для построения графика функции у = cos х ученикам напоминается формула приведения cos х= sin (х+π/2), которая свидетельствует о том, что графики функций у= cos х и у= sin (х+π/2) являются тождественно равными. Для построения графика функции у= sin (х+π/2) стоится координатная плоскость, на оси абсцисс которой отмечается точка –π/2. Если взять эту точку за начало координат для построения графика sin х, то этот график является и графиком функции у= sin (х+π/2) для начала координат. То есть график функции у = cos х является на π/2 сдвинутым по оси абсцисс графика функции у= sin х. очевидно, что графиком функции у = cos х также является синусоида. Ее расположение позволяет сделать выводы о свойствах функции.
Первое свойство функции – об области определения. Очевидно, что областью определения функции будет вся числовая прямая, то есть D(f)=(- ∞;+∞).
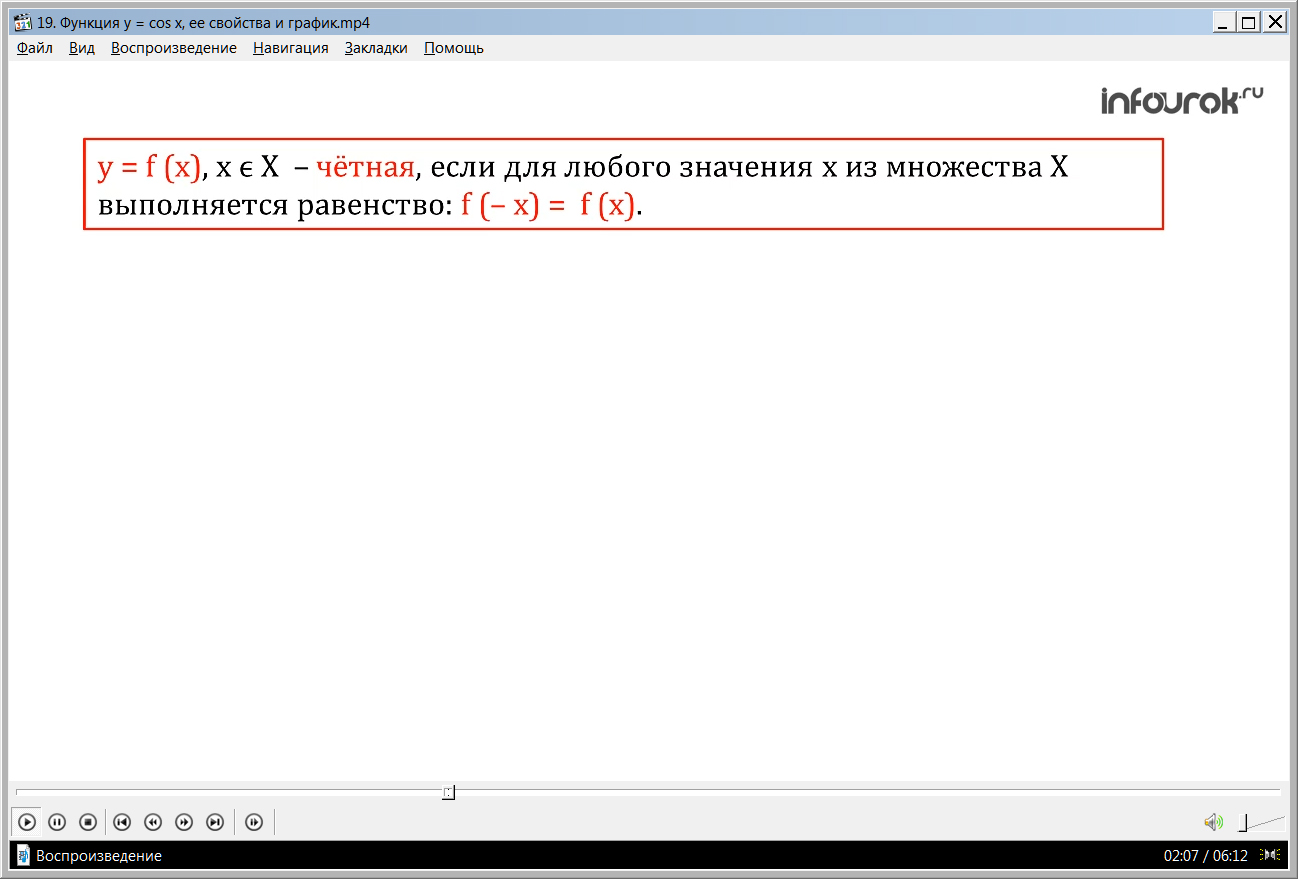
Во втором свойстве функции отмечается четность функции. Ученикам напоминается изученный в 9 классе материал, в котором было указано условие четности функции. Для четной функции является справедливым равенство f(-x)=f(x). Говоря о четности функции косинуса, нужно отметить, что график этой функции симметричен относительно оси ординат. Продемонстрировать свойства функции можно на рисунке, где изображена на координатной плоскости единичная окружность. В первой и четвертой четвертях отмечены точки, симметричные относительно оси абсцисс. Косинус определяется абсциссой точки, поэтому для двух точек L(t) и N(-t) абсциссы одинаковые. Поэтому cos (-t)= cos t.
Третье свойство отмечает промежутки убывания и возрастания функции. В свойстве указано, что функция убывает на отрезке [0;π], а на отрезке [π;2π] косинус возрастает. На рисунке продемонстрирован график функции, на котором хорошо видно область убывания и возрастания функции.
Очевидно, что функция у = cos х возрастает на каждом отрезке [π+2πk;2π+2πk]. Отрезки убывания в общем виде выглядят так [2πk;π+2πk], где k – целое число.
В четвертом свойстве отмечается ограниченность функции косинуса сверху и снизу. Аналогично синусу, можно отметить ограниченность значений косинуса -1<= cos х<=1. Поэтому функция является ограниченной.
В пятом свойстве указано наименьшее и наибольшее значения функции. При этом наименьшее значение -1 достигается в любой точке х= π+2πk, а наибольшее значение 1 достигается в любой точке х=2πk.
Шестое свойство указывает на непрерывность функции у = cos х. На рисунке, где изображен график, видно, что данная функция не имеет разрывов на всей области определения.
В седьмом свойстве функции указано, множество значений у = cos х располагается на отрезке [-1;1].
Далее рассматриваются примеры, в которых необходимо использовать знания о свойствах функции у = cos х. В первом примере необходимо решить уравнение cos х=1-х2. Решением данного уравнения будут точки пересечения графиков функций, которые представлены выражениями правой и левой части уравнения, то есть у = cos х и у=1-х2. Очевидно, что график первого уравнения – синусоида, продемонстрированная в теме ранее. График второй функции – парабола, вершина которой располагается в точке (0;1). Построив графики каждой функции, на рисунке к данной задаче видно, что единственной точкой пересечения двух графиков будет точка В(0;1).
Во втором примере необходимо построить и прочитать график функции, которая определяется на отрезке х<π/2 выражением sinx, а на отрезке х>=π/2 выражением cosx. На рисунке, сопровождающем решение примера, строится график функции у=sinx на отрезке [-3π/2; π/2]. При этом в точке π/2 функция не принимает значение. На отрезке [π/2; 3π/2] строится фрагмент функции у = cos х. Очевидно, построенные фрагменты будут повторяться по всей области определения. Далее описывается, как читается функция. Отмечается, что это означает описать ее свойства. Перечисляются свойства данной функции – область определения (-∞;+∞), отсутствие признаков четности или нечетности для всей области определения, ограниченность функции и сверху, и снизу. Наибольшим значением функции будет 1, а наименьшим -1. Также отмечается наличие разрыва в точке х=π/2, множество значений функции (-1;1).
Видеоурок «Функция у = cos х, ее свойства и график» применяется на уроке математики по данной теме в качестве наглядного материала. Также данное видео может быть полезным для формирования необходимых умений у учеников учителю, который проводит обучение дистанционно. Материал может быть рекомендован для самостоятельного рассмотрения ученикам, которые недостаточно хорошо освоили тему и требуют дополнительных занятий.
ТЕКСТОВАЯ РАСШИФРОВКА:
Прежде чем построить график функции у = cos x, вспомним формулу приведения, по которой cos x = sin( x + 14ПЂ2)"> (косинус аргумента икс равен синусу аргумента икс плюс пи на два). Это значит, что функции у = cos x и
у = sin( x + <!--?mso-application progid="Word.Document"?--> 14ПЂ2)"> тождественно равны, следовательно их графики совпадают.
Для построения графика функции у = sin( x + <!--?mso-application progid="Word.Document"?--> 14ПЂ2)"> нам понадобится вспомогательная система координат с началом в точке В( - <!--?mso-application progid="Word.Document"?--> 14ПЂ2"> ; 0) ( в точке бэ с координатами минус пи на два , ноль).Если в новой системе координат построить график функции у = sin x, то получим график функции
у = sin( x + <!--?mso-application progid="Word.Document"?--> 14ПЂ2)"> или же график функции у = cos x, так как их графики совпадают( смотри рис.1).
Поскольку график функции у = cos x получается из графика синуса с помощью параллельного переноса на расстояние <!--?mso-application progid="Word.Document"?--> 14ПЂ2"> в отрицательном направлении, то график этой функции также является синусоидой.
Изображение графика функции у = cos x дает наглядное представление о свойствах этой функции .
СВОЙСТВО 1. Область определения – множество всех действительных чисел или D (f) = ( - <!--?mso-application progid="Word.Document"?--> 14в€ћ"> ; + <!--?mso-application progid="Word.Document"?--> 14в€ћ"> ) ( дэ от эф равно промежутку от минус бесконечности до плюс бесконечности).
СВОЙСТВО 2. Функция у = cos x четная.
На уроках в 9 классе мы изучили, что функция у = f (x), х ϵХ ( игрек равно эф от икс, где икс принадлежит множеству икс большое) называется четной, если для любого значения х из множества Х выполняется равенство
f (- x) = f (x)( эф от минус икс равно эф от икс).
СВОЙСТВО 3.На отрезке [ 0 ; π ]( от нуля до пи) функция убывает, возрастает на отрезке [ π ; 2π ] ( от пи до двух пи) и так далее.
Можно сделать общий вывод: функция у = cos x возрастает на отрезке
[π <!--?mso-application progid="Word.Document"?--> 14+2ПЂk "> ; <!--?mso-application progid="Word.Document"?--> 142ПЂ+2ПЂk"> ] ( от пи плюс два пи ка до двух пи плюс два пи ка), а убывает на отрезке [ <!--?mso-application progid="Word.Document"?--> 14 2ПЂk"> ; <!--?mso-application progid="Word.Document"?--> 14ПЂ+2ПЂk]"> ( от двух пи ка до пи плюс два пи ка), где ( ка принадлежит множеству целых чисел).
СВОЙСТВО 4.Функция ограничена сверху и снизу.
СВОЙСТВО 5. Наименьшее значение функции равно минус единице и достигается в любой точке вида х = <!--?mso-application progid="Word.Document"?--> 14ПЂ+2ПЂk"> ( или можно записать унаим.= - 1); наибольшее значение равно 1 и достигается в любой точке вида х = <!--?mso-application progid="Word.Document"?--> 142ПЂk">
( или можно записать унаиб.= 1).
СВОЙСТВО 6.Функция у = cos x является непрерывной.
СВОЙСТВО 7. Множество значений функции – отрезок от минус одного до одного( или можно записать Е(f) = [ - 1; 1] ).
Рассмотрим примеры.
ПРИМЕР 1.Решить уравнение cos x= 1 – х2( косинус икс равно один минус икс в квадрате).
Решение. Решим это уравнение графически. В одной системе координат построим два графика функций: у = cos x и у = 1 – х2. Графиком функции
у = 1 – х2 является парабола, ветви которой направлены вниз, так как коэффициент при икс в квадрате отрицателен. ( см. рис.2) У построенных графиков только одна общая точка – это точка В( 0; 1)( бэ с координатами ноль, один).
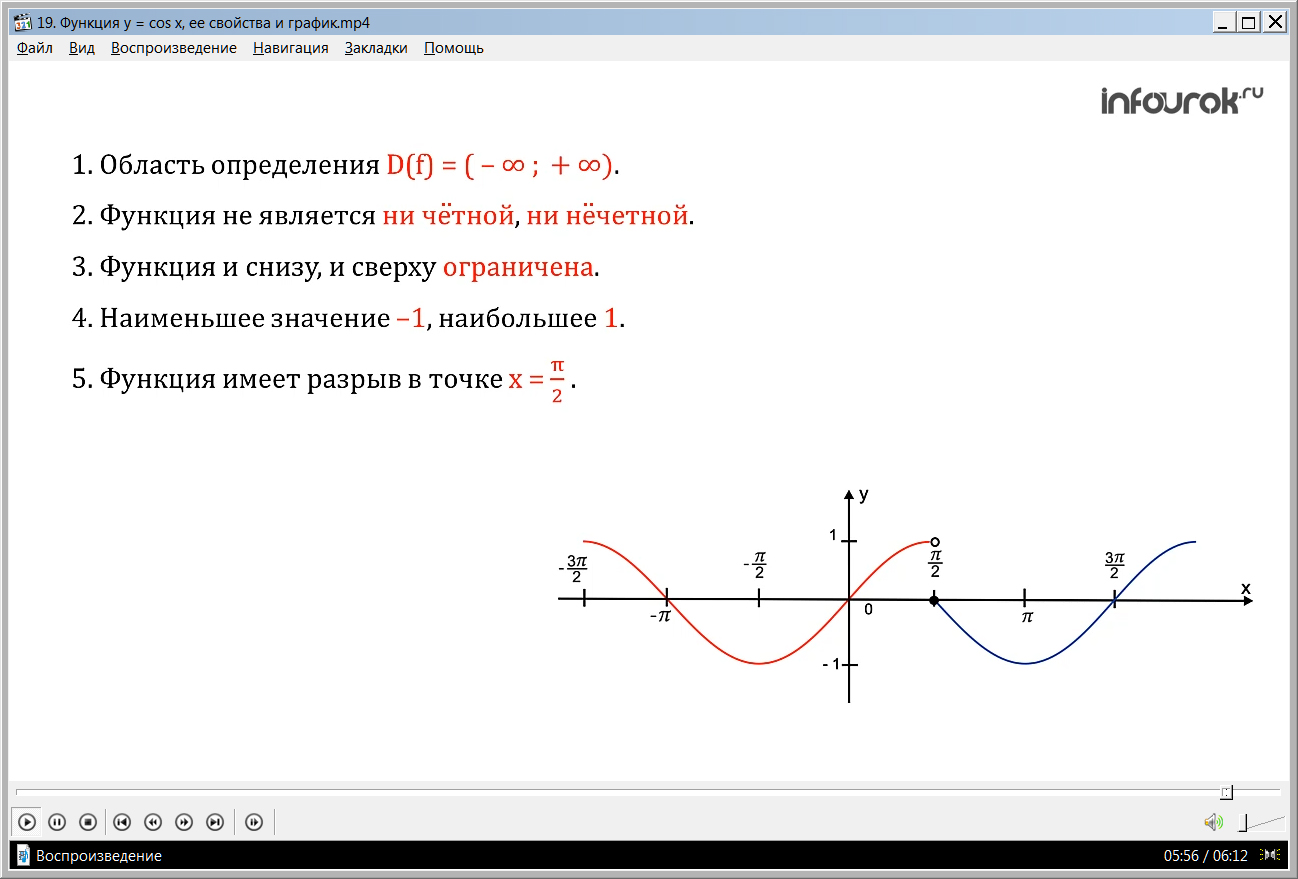
ПРИМЕР 2. Построить и прочитать график функции у = f( x), где
Решение. Строить график будем «по кусочкам». Сначала построим часть графика функции у = sin x на открытом луче ( - <!--?mso-application progid="Word.Document"?--> 14в€ћ"> ; <!--?mso-application progid="Word.Document"?--> 14ПЂ2"> ) , затем в этой же системе координат на луче [ <!--?mso-application progid="Word.Document"?--> 14 ПЂ2"> ; + <!--?mso-application progid="Word.Document"?--> 14в€ћ"> ) построим часть графика функции у = cos x. Получим график функции у = f( x).
Прочитаем график этой функции (это значит перечислим свойства функции):
- Область определения – множество всех действительных чисел, т.е.
D(f) = ( - <!--?mso-application progid="Word.Document"?--> 14в€ћ ; + в€ћ)"> ( т.е. дэ от эф равно промежутку от минус бесконечности до плюс бесконечности).
- Функция не является ни четной, ни нечетной.
- Функция и снизу, и сверху ограничена.
- Наименьшее значение функции равно минус один ( таких точек бесконечно много) , наибольшее значение функции равно единице( таких точек тоже бесконечно много) .
- Функция имеет разрыв в точке х = <!--?mso-application progid="Word.Document"?--> 14ПЂ 2"> .
- Множеством значений функции является отрезок от минус единицы до единицы.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 18596 |
| Номер материала | 842 |