
Урок "График гармонического колебания"

Краткое описание документа:
В видеоуроке «График гармонического колебания» рассматривается тема, каким образом с помощью тригонометрической функции можно описать физический процесс гармонического колебания.
В начале урока приводится пример колебания с грузом на пружине, который вывели из положения равновесия. Процесс колебания можно увидеть на анимированном рисунке.
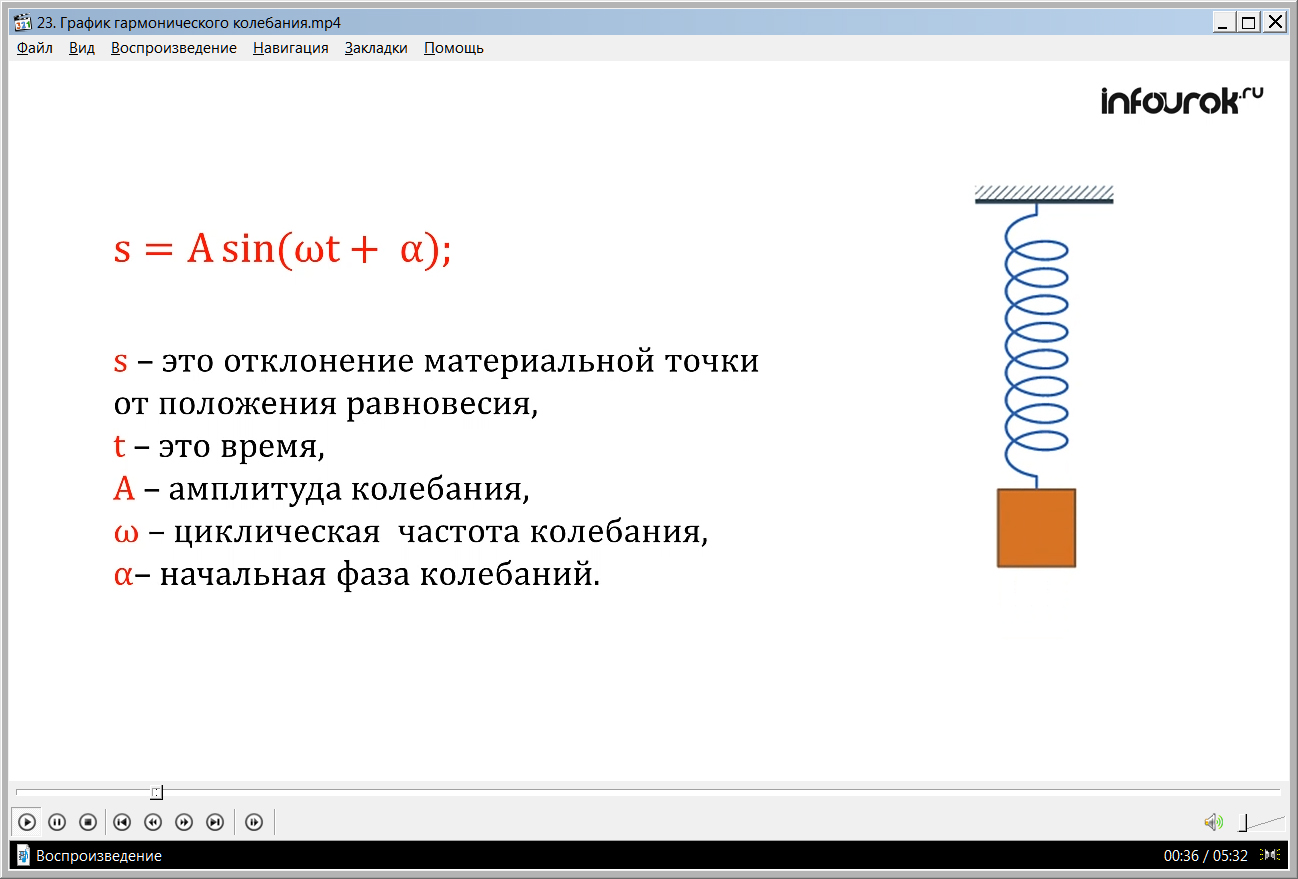
Уравнение гармонического колебания можно представить в виде:
s= Asin (ωt + α), где
s – отклонение – координата точки;
A – амплитуда колебания;
α – начальная фаза;
ω – частота;
t – время.
Приводится пример – построение графика функции s = 2 sin (3t + 3 π/4). Путем преобразования получим формулу s = 2 sin 3 (t + π/4). Для построения графика применим следующий алгоритм:
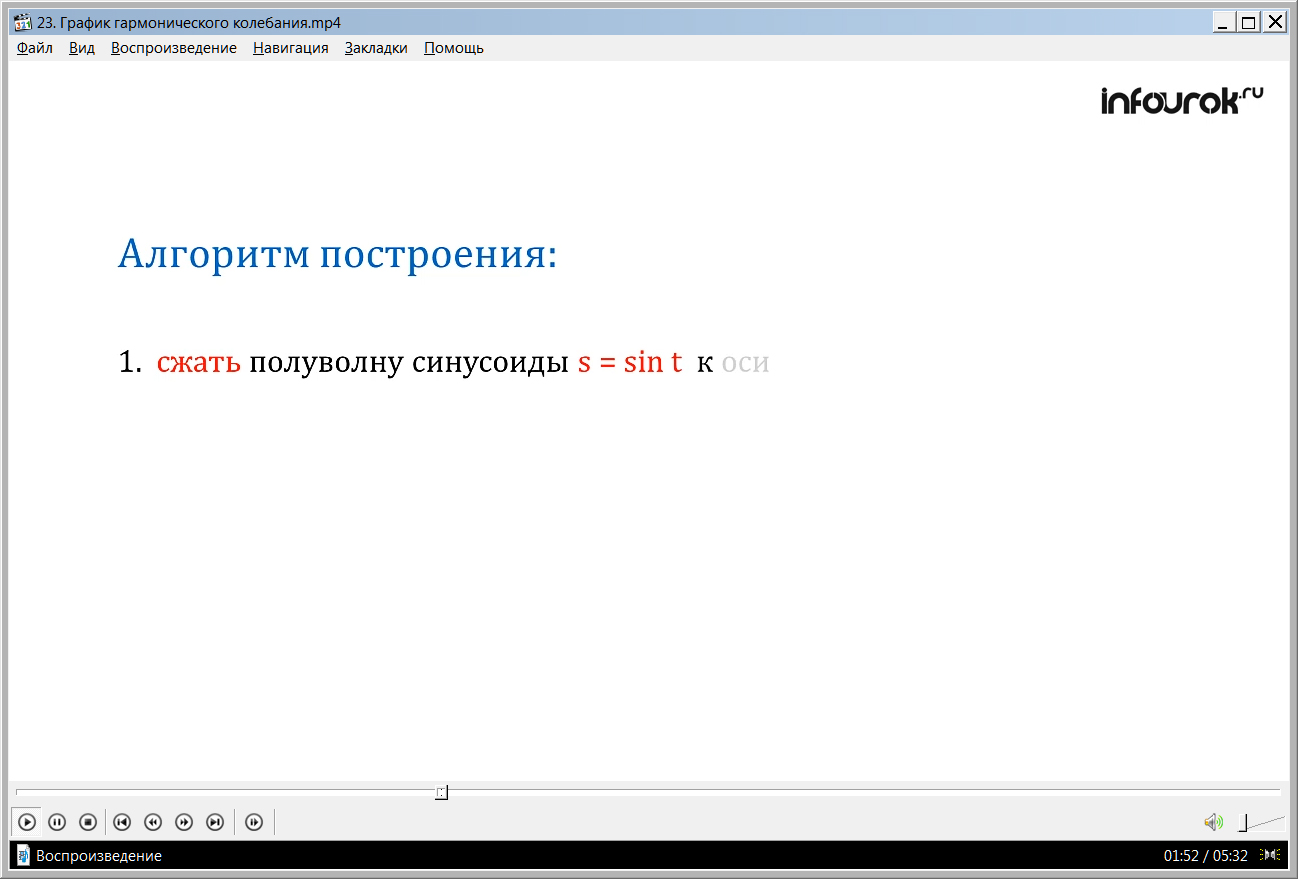
1) сжатие части волны графика s = sintк оси ординат, где коэффициент сжатия равен 3;
2) растяжение части волны от оси абсцисс, где коэффициентом растяжения будет равен 2;
3) сдвиг части волны по оси абсцисс наπ/4 влево;
4) построение всего графика.
Для построения такого графика также необходимо найти точки пересечения с осью абсцисс. Для этого решаем уравнение 2 sin 3 (t + π/4)= 0. Зная, что решением уравнения sint = 0 является t = πk,находим значениеt= - π/4 + πk/3.
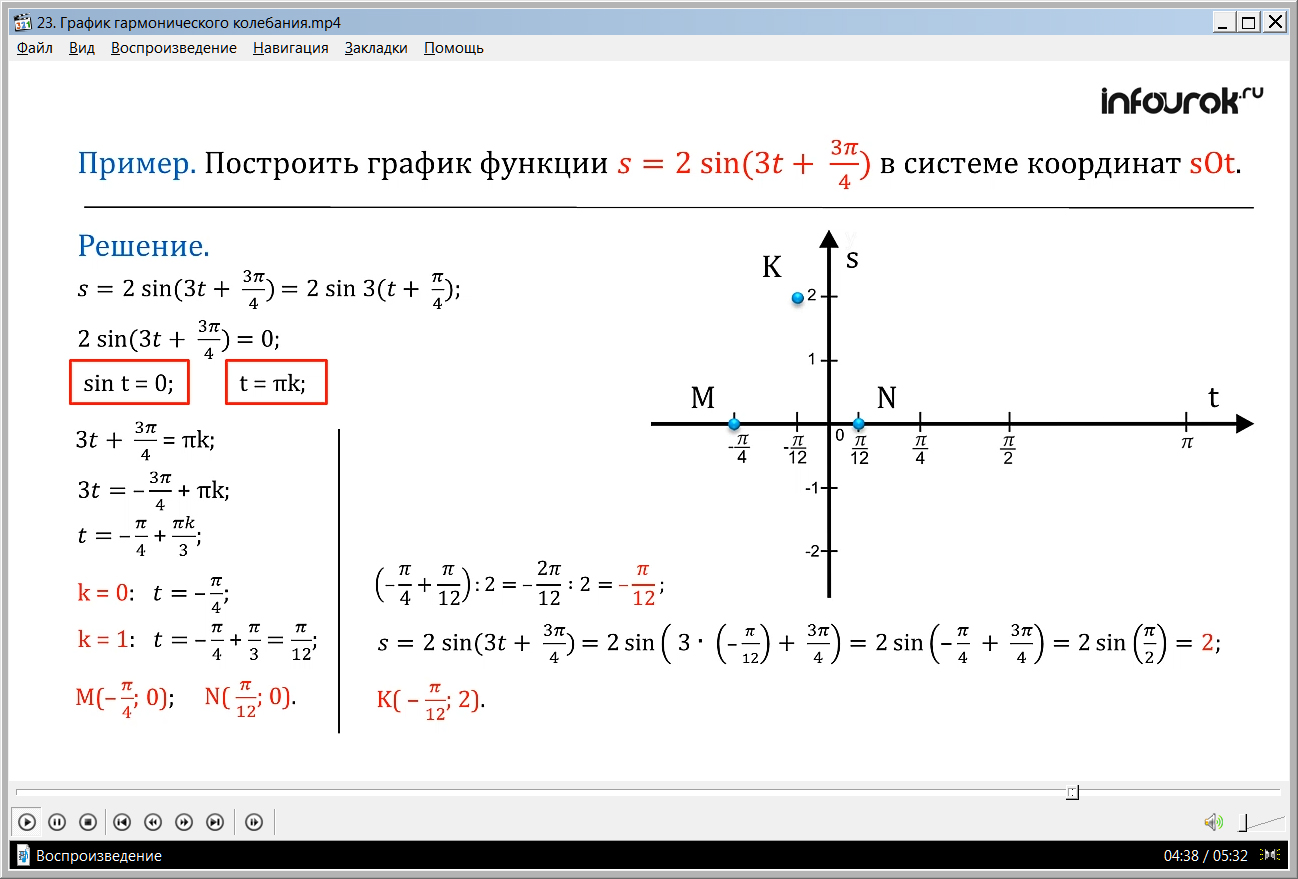
Для нахождения точек на оси х найдем значения tпри k = 0и при k = 1. Точки M (- π/4; 0) и N (π/12; 0) являются точками пересечения графика с осьюx.Находим координаты середины части волны графика:
1) координата х – это среднее арифметическое координат начала и конца волны - π/4 иπ/12, равна - π/12.
2) подставив значение х = - π/12в функциюs = 2 sin (3t + 3 π/4), найдем s = 2.
Следовательно, мы получили точку K (- π/12; 2) – середину полуволны искомого графика. С помощью точек M, N и K построим часть волны графика и затем весь график.
Подводя итог, укажем, что в рассмотренной функции гармонического колебанияs = 2 sin (3t + 3 π/4):
– амплитуда А = 2;
– циклическая частота колебания ω = 3;
– начальная фаза колебаний α =3 π/4.
Амплитуда – это максимальное и минимальное значение переменной s, что мы можем увидеть на построенном графике.
Итак, видеоурок по данной теме наглядно показал, как с помощью тригонометрии можно описать физический процесс гармонического колебания. В ходе изучения урока учащиеся познакомились с законом гармонического колебания и его величинами, научились строить график функции гармонического колебания.
Видеоматериал может быть полезным учителю при проведении урока, а также ученикам при самостоятельном изучении данной темы.
ТЕКСТОВАЯ РАСШИФРОВКА:
С помощью тригонометрических функций можно описать различные процессы. Рассмотрим, использование тригонометрической функции для описания процесса колебания. Если груз, висящий на пружине, вывести из положения равновесия, то он начнет совершать вертикальные колебания, при чем закон движения будет выражаться формулой: s = Asin() ( эс равно а, умноженное на синус суммы омега, умноженное на тэ, и альфа). Эту формулу называют законом ( или уравнением) гармонических колебаний. В уравнении гармонических колебаний все величины имеют физический смысл: s – это отклонение материальной точки от положения равновесия, - это время,
А - амплитуда колебания ( то есть максимальное отклонение от положения равновесия), ( омега) – циклическая (или круговая) частота колебания, ( альфа) – начальная фаза колебаний.
Рассмотрим ПРИМЕР. Построить график функции s = 2sin(3t+ ) ( эс равно удвоенному синусу суммы трех тэ и трех пи на четыре) в системе координат sOt( эс о тэ).
Решение. Преобразуем данную формулу: вынесем три за скобку, получим:
s = 2sin(3t+) = 2sin3(). Для построения графика такой функции нужно к графику функции s = sin применить следующие преобразования:
1) сжать полуволну синусоиды s = sin к оси ординат с коэффициентом 3;
2) растянуть от оси абсцисс с коэффициентом 2;
3) полученную полуволну сдвинуть вдоль оси абсцисс на (пи на четыре) влево.
С помощью полученной главной полуволны искомого графика построим весь график.
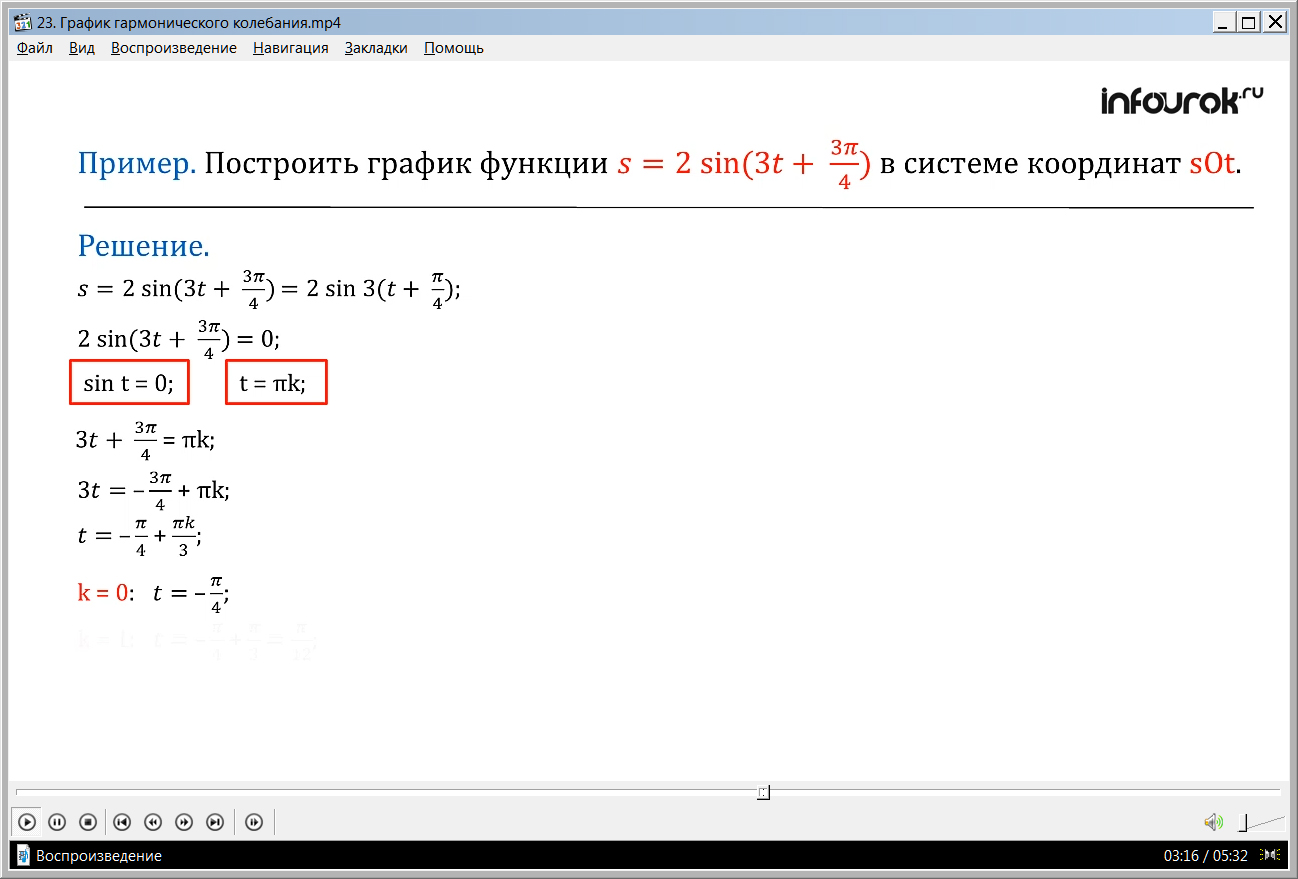
Но, чтобы построить такой график на практике, нам нужно знать точки пересечения с осью абсцисс. Для этого решим уравнение: 2sin(3t+) = 0 (удвоенный синус суммы трех тэ и трех пи на четыре равен нулю). Нам известно, что решение уравнения sin t = 0( синус тэ равно нулю) имеет вид
t= πk ( тэ равно пи ка), поэтому имеем
Три тэ плюс три пи, деленное на четыре, равно пи ка.
Три пи, деленное на четыре переносим в правую сторону с противоположным знаком.
Получаем: три тэ равно минус три пи, деленное на четыре, плюс пи ка.
Вычислим значение тэ, выражение минус три пи, деленное на четыре, плюс пи ка разделим на три.
Тэ равно сумме минус пи, деленное на четыре, и пи ка, деленное на три.
Для нахождения точек на оси абсцисс, которые служат концами одной полуволны, дадим параметру k значения 0 и 1. Получим при k=0 = - ( ка равном нулю тэ равно минус пи, деленное на четыре), а при k= 1 получим
= - + = ( тэ равно пи на двенадцать). Получили точки M (- ; 0) (эм с координатами минус пи на четыре, ноль) и N(; 0) ( эн с координатами пи на двенадцать, ноль). Среднее арифметическое чисел - и равно - , так как (- + ׃ 2 = - ׃ 2 = - (сумма минус пи на четыре и пи на двенадцать, деленная пополам, равна минус пи на двенадцать). Следовательно, серединой отрезка [- ; является точка - (минус пи на двенадцать). Найдем значение заданной функции в точке - (минус пи на двенадцать), имеем
s = 2sin(3t+)= 2sin()= 2sin()= 2sin = 2 ( эс равно удвоенному синусу суммы трех тэ и трех пи на четыре равно удвоенному синусу суммы произведения трех и минус пи на двенадцать и трех пи на четыре равно удвоенному синусу суммы минус пи на четыре и трех пи на четыре равно удвоенному синусу пи на два , а это равно двум). Следовательно, точка K (- ; 2) ( ка с координатами минус пи на двенадцать и два) – верхняя точка искомой полуволны. По точкам M, N и K сначала построим полуволну искомого графика, а затем и весь график
В рассмотренном примере амплитуда колебаний равна двум А = 2, частота колебаний равна трем ( омега ), а начальная фаза колебаний равна три пи на четыре ( альфа).
А, и являются физическими величинами, которые характеризуют процесс гармонических колебаний, в каждом определенном процессе они задаются определенные, можем утверждать что амплитуда это максимальное и минимальное значение переменной s, но все это работа физики. Наша задача была охарактеризовать график гармонических колебаний.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 12905 |
| Номер материала | 851 |