
Урок "Исследование числовых функций"

Краткое описание документа:
Тема «Исследование функций» является одной из ключевых в школьном курсе математики. Изучение данной темы начинается с самого начала знакомства с алгеброй. По мере изучения все большего числа функций и их свойств границы исследования функций все более расширяются. Урок, который проходит в 10 классе, связанный с исследованием функций, подразумевает, что обучающиеся имеют все необходимые знания.

Данный урок можно использовать на обычном уроке алгебры в 10 классе на этапе объяснения нового материала. Он занимает всего 8:03 минут. Примерно столько же времени уходит на объяснение материала учителем. Главным достоинством этого видеоурока является то, что во время объяснения материала не будет никаких отступлений от темы, и все пройдет по намеченному плану. А главное, обучающиеся хорошо усвоят материал.
И в начале урока автор поясняет, что значит исследовать функцию.
Так как исследование функции заключается в описании ее свойств, то автор начинает этот процесс с определения четности функции. Для этого предлагается вспомнить три шага. Далее следует два примера на определение четности функции.
Затем, когда определена четность функции, необходимо исследовать ее на монотонность. Это исследование состоит их пяти шагов. Каждый из них автор подробно описывает и ведет математическую запись, что, в свою очередь, оказывает положительное влияние на формирование математической грамотности. Объяснение материала сопровождается иллюстрациями. И к этому пункту прилагается пример.
Далее автор предлагает познакомиться с общей схемой исследования функции, в которую входит семь пунктов. Для начала необходимо найти область определения и область значений функции, затем исследовать ее на четность и периодичность, далее найти нули и промежутки знакопостоянства, исследовать на монотонность и ограниченность, и, наконец, найти наибольшее и наименьшее значения функции.
Далее предлагается провести исследование линейной функции и обратной пропорциональности в общем виде. Исследование этих функций ведется по очереди. Сначала исследуется линейная функция, а затем обратная пропорциональность. Каждое свойство описывается подробно. Поэтому обучающиеся должны легко и сразу понять, о чем говорится здесь.
Видеоурок может использоваться учителем в качестве объяснения нового материала. А также самими обучающимися в качестве средства самостоятельного обучения алгебре и началам анализа.
ТЕКСТОВАЯ РАСШИФРОВКА:
Исследование числовых функций.
Исследовать функция значить определить какими свойствами она обладает
Чтобы ответить на этот вопрос, нужно, вспомнить алгоритм исследования функции
игрек равно эф от икс на четность.
Рассмотрим пример.
Исследовать функции на четность:
Первая функция. Эф от икс равно икс в четвертой степени плюс дробь, в числителе которой два, а в знаменателе икс в шестой степени.
Первое. Функция определена при всех значениях икс, кроме икс равное нулю. Значит, область определения- симметричное множество.
Второе. Находим эф от минус икс.
Третье. Имеем, что для любого икс из области определения выполняется равенство эф от минус икс равно эф от икс.
Делаем вывод, что функция
четная.
Вторая функция.
Игрек равен квадратный корень из выражения икс минус три. Эта функция определена на луче от трех до плюс бесконечности. Этот луч – несимметричное множество, значит, функция не является ни четной, ни нечетной.
Как исследовать функцию на монотонность?
Пауза.
Алгоритм исследования функции игрек равно эф от икс на монотонность.
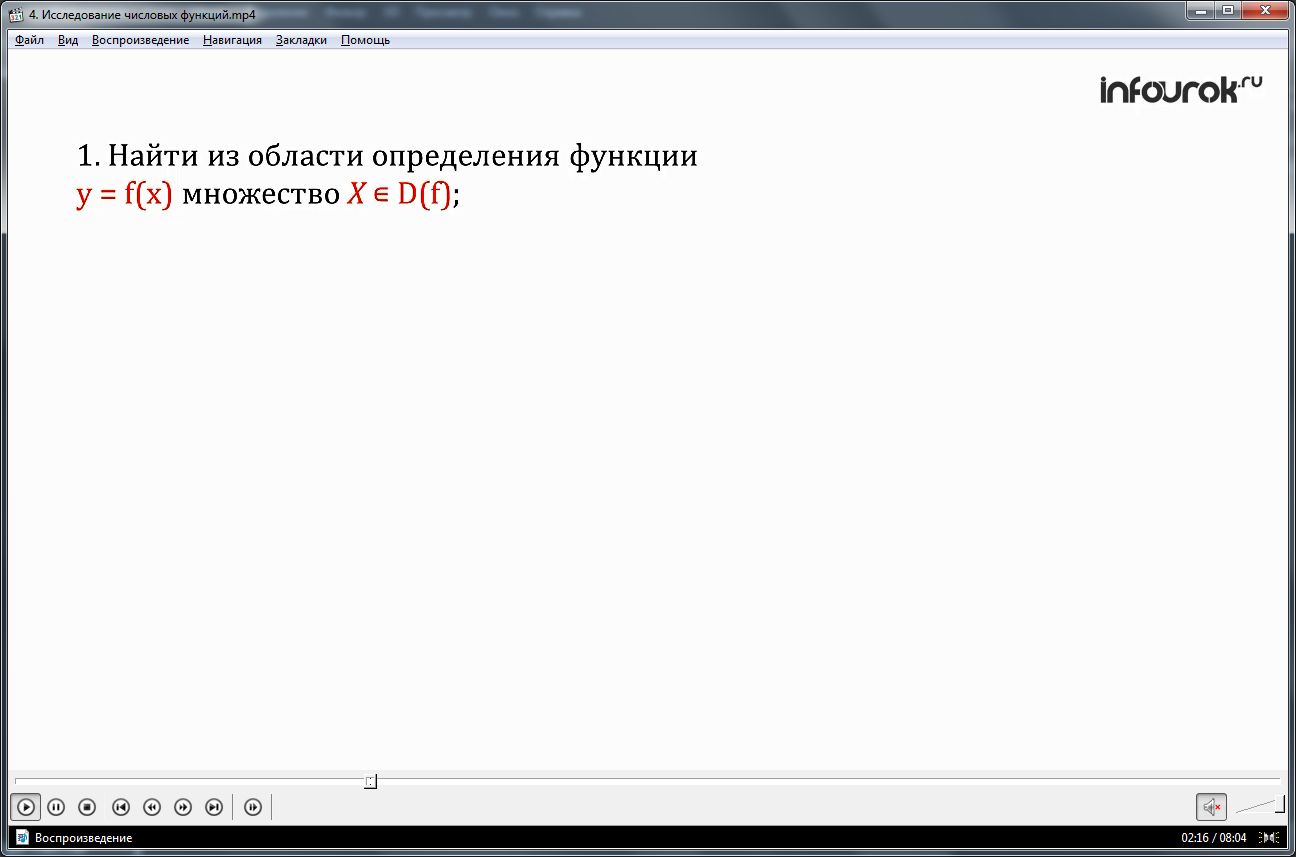
1.Найти из области определения функции
игрек равно эф от икс множество икс большое, на котором рассматривается монотонность из области определения функции.
2.Выбрать произвольные значения аргумента для любых икс первое из множества икс большое и икс второе из множества икс большое таких,что икс второе больше икс первого.
- Найти значения эф от икс первое и эф от икс второе и сравнить их.
4.Если выполняется неравенство эф от икс второе больше эф от икс первое, то функция возрастает на множестве икс большое.
Другими словами – большему значению аргумента соответствует большее значение функции.
5.Если при условии, что икс второе больше икс первое выполняется неравенство эф от икс второе меньше эф от икс первое, то функция убывает на множестве Х.
Другими словами – большему значению аргумента соответствует меньшее значение функции.
Например. Исследуем функцию эф от икс равно три минус пять икс на монотонность.
Решение.
Во – первых, находим область определения функции – это множество всех чисел;
Во – вторых, выбираем два произвольных значения аргумента из области определения, такие, что второе больше первого.
Третье, подставляем выбранные значения аргумента соответственно в формулу функции и используя свойства неравенств, приходим к выводу: большему значению аргумента соответствует меньшее значение функции. Значит функция убывающая.
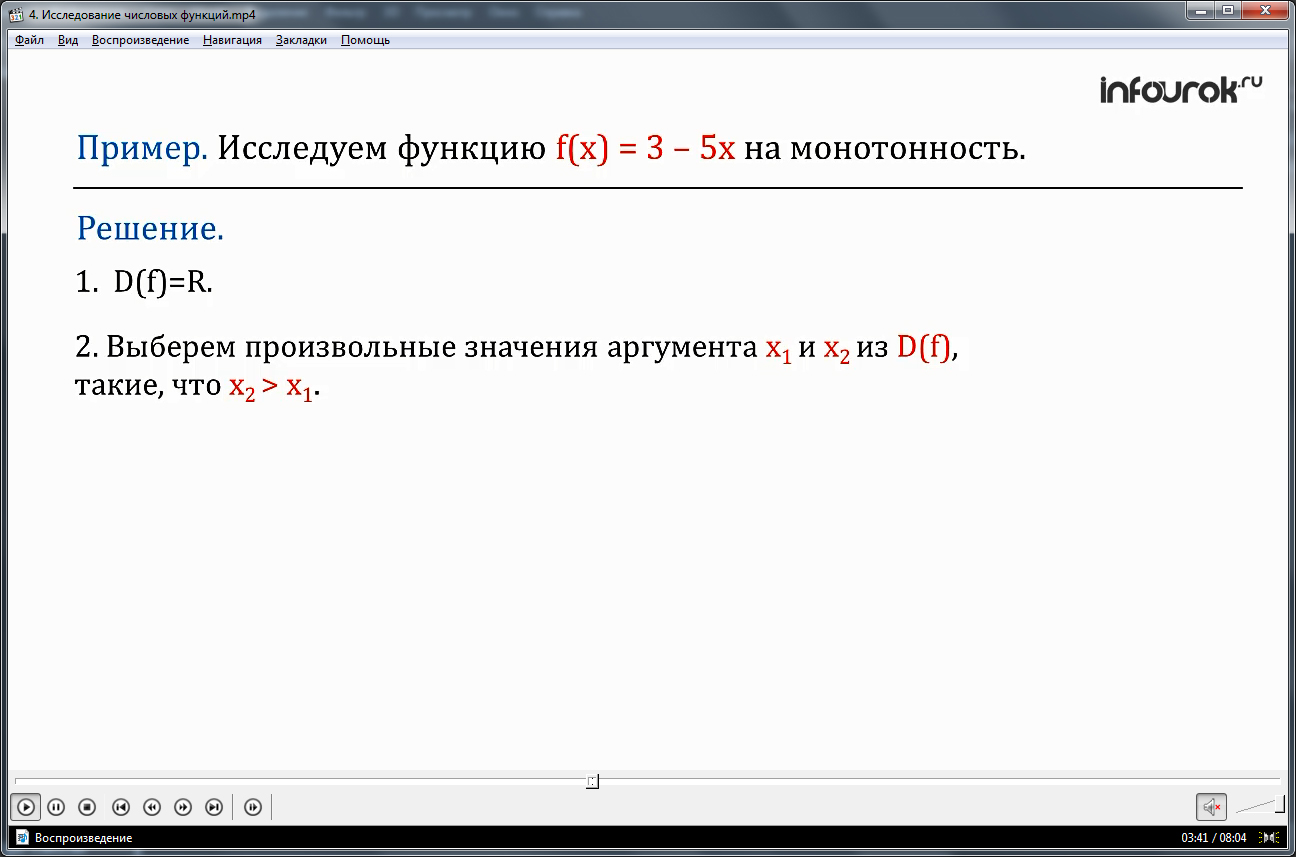
Схема исследования функции с помощью
ее свойств выглядит следующим образом:
1.Найти область определения и значений
данной функции.
2. Исследовать функцию на четность или
нечетность, периодичность.
3. Найти нули функции.
4. Найти промежутки знакопостоянства
функции.
5. Выяснить на каких промежутках функция
возрастает, а на каких убывает.
6.Выяснить ограниченность функции;
7. Найти наибольшее и наименьшее
значения функции
Этот план имеет примерный характер.
Но его нужно придерживаться.
Проведем исследование функций
у=kx + bи y=
Рассмотрим функцию
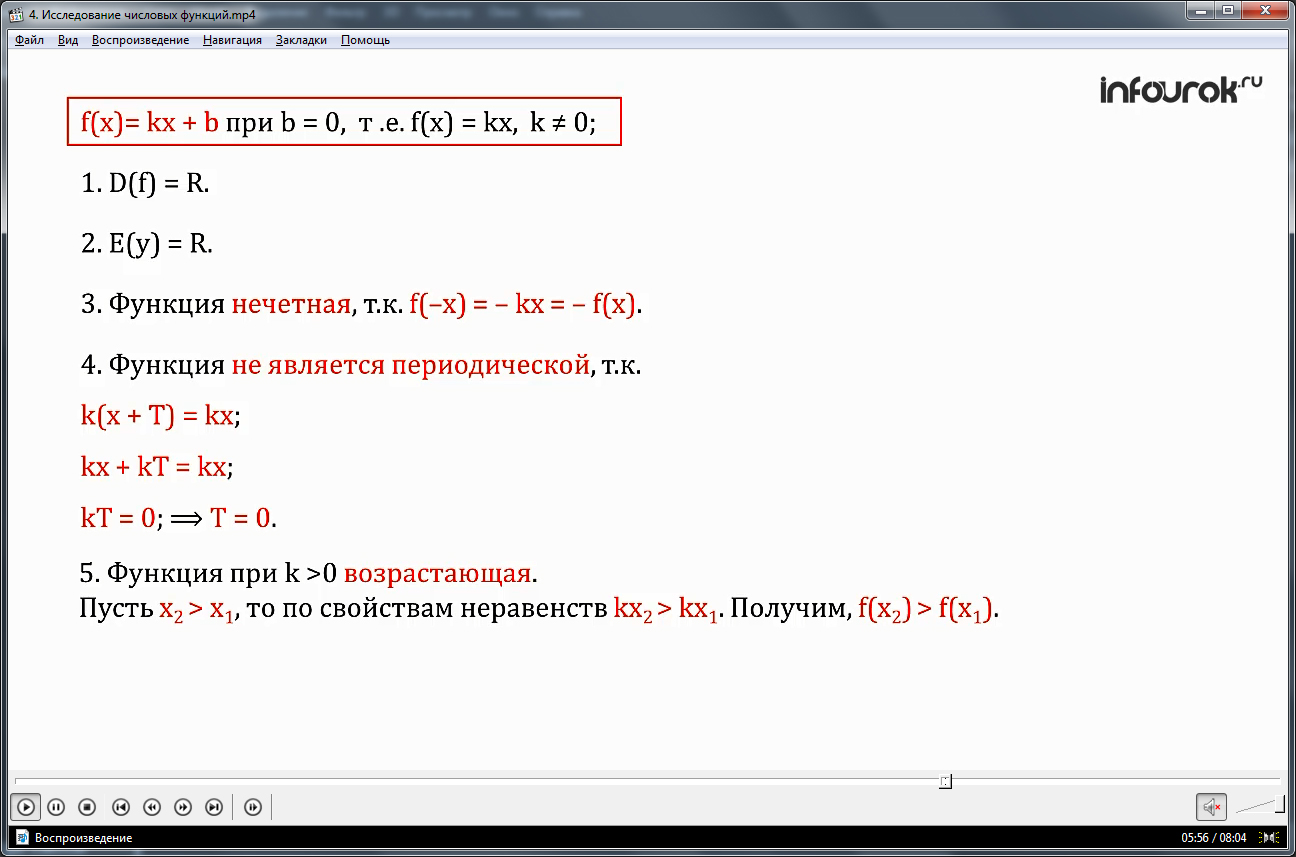
эф от икс равно ка икс плюс бэ при бэ равное нулю, то есть эф от икс равно ка икс ,при ка не равное нулю.
1,2)Область определения и область значений множество всех чисел.
3) Функция является нечетной, т.к. f(-х)=
- kх= - f(х).
4)Функция не является периодической, так как k(х+Т)=kх;
kх + kТ=kх;
kТ=0; отсюда получаем Т=0.
5) Функция при k >0 возрастающая.
Действительно, пусть х2 > х1;то по свойствам неравенств kх2 > kх1. Получим,f(х2) > f(х1). Аналогично можно доказать, что при k< 0, функция убывающая.
.Не ограниченная. Если икс равен нулю, то и игрек равен нулю.
Рассмотрим функцию
эф от икс равно ка деленное на икс при ка не равное нулю.
1,2) Функция определена всюду, кроме х = 0, то есть
Область определения и область значений объединение двух интервалов от минус бесконечности до нуля и от нуля до плюс бесконечности.
3) Функция определена всюду, кроме х = 0, то есть D(f)=(-∞;0)(0;+∞).
4) рассмотрим у=f(x) при ка больше нуля
Пусть х2 > х1 ,тогда х2 -х1>0 а - <0,
Значит, f(х2) -f(х1)= - = к( - )
При к>0 f(х2) -f(х1) <0, функция убывающая
а при к<0 (при ка меньше нуля) f(х2) -f(х1)>0 – возрастающая
5)При ка больше нуля функция принимает положительные значения на интервале от нуля до плюс бесконечности и отрицательные на интервале от минус бесконечности до нуля.
При ка меньше нуля функция принимает положительные значения на интервале
от минус бесконечности до нуля и отрицательные на интервале от нуля до плюс бесконечности.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 3878 |
| Номер материала | 827 |