
Урок "Изучение графика числовых функций"

Краткое описание документа:
Каждый старший школьник должен уметь читать графики числовых функций. Такие навыки начинают отрабатываться с момента знакомства с графиками в курсе математики. К 10 классу эти умения должны получить достаточно устойчивый уровень. Хотя с самим понятием чтения графиков, в более глубоком смысле, обучающиеся знакомятся именно в 10 классе. И в помощь учителю, который собирается объяснять материал по данной теме, разработан данный видеоурок.
Здесь содержится полезная, полная и качественная информация, усвоение которой не затруднено ничем. Обучающиеся легко освоят материал по теме, так как он подобран в соответствии со рядом требований, в том числе по возрасту обучающихся.
Урок длится 5:32 минут. Практически столько же времени, если не отвлекаться на какие-то посторонние моменты, понадобится учителю, чтобы объяснить новый материал на уроке. Здесь же время строго регламентировано. Поэтому пока обучающиеся будут просматривать видеоурок, у них не будет времени отвлекаться, иначе они не поймут суть происходящего. Так с помощью данного урока можно сформировать у обучающихся такие качества, как внимательность, дисциплинированность и самостоятельность.
Автор урока обращает внимание слушателей на то, что чтение графиков числовых функций имеет широкое применение в нашей жизни. Особенно часто чтение графиков используется в экономике. При этом на экране изображен график некоторой функции.
Здесь же автор предлагает вспомнить, какая функция называется числовой. Пока обучающиеся начинают вспоминать, он напоминает им данное понятие. При этом объяснение сопровождается иллюстрацией. При этом, получается, что необходимо также вспомнить, что называется областью определения и областью значений функции. Автор напоминает и то, как выглядит уравнение функции в общем виде.
Чтобы обучающимся было проще понять принцип чтения графиков функций, необходимо вспомнить, что называется аргументом, то есть зависимой переменной, и независимой переменной. После этого предлагается рассмотреть некоторую произвольную функцию и построить ее график, подобрав пары чисел, которые являются координатами точек в системе координат. Когда график построен, вводится определение графика функции.
Далее автор говорит, что означает прочитать график функции. Получается, что для этого необходимо перечислить ее свойства, которые видны по графику. При этом перечисляются те свойства, которыми обладают все функции, и те, которыми обладают только некоторые функции.
Затем предлагается рассмотреть в качестве примеров, известные функции, которые были изучены в курсе алгебры ранее. Таких функций рассматривается две, последовательно. Сначала на экране изображается график функции, а затем подробно описывается каждое свойство, которым обладает функция. На каждом пункте автор останавливается и поясняет, что и как получается.
На этом видеоурок завершается, но не заканчивается занятие в школе. Поэтому оставшееся время желательно посвятить закреплению материала, подобрав для этого необходимые задания.
Урок будет полезен как для учителей, так и для обучающихся.
ТЕКСТОВАЯ РАСШИФРОВКА:
Чтение графика числовой функции.
Чтение графиков функций имеет большое практическое значение. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.
Для изучения сегодняшней темы нам необходимо вспомнить: какая функция называется числовой?
Пауза
Числовой функцией называется правило, с помощью которого каждому элементу из множества икс большое мы ставим в соответствие единственный элемент из множества игрек большое.
Множество Х называется областью определения функции.
Множество У называется множеством значений функции.
Равенство игрек равен эф от икс называется уравнением функции.
икс - независимая переменная, или аргумент функции. игрек - зависимая переменная.
А что называется графиком функции?
Если дана функция игрек равно эф от х, где икс принадлежит икс большому и возьмем все пары икс, игрек и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции – это графической изображение зависимости между множествами икс большое и игрек большое.

Прочитать график - это значит перечислить свойства функции,
а именно:
1)область определения функции;
2)область значений функции;
3)нули функции – значения аргумента, при которых функция равна нулю;
4)промежутки знакопостоянства функции, т.е.промежутки,
где значения функции имеют один и тот же знак;
5)промежутки монотонности функции, т.е. промежутки, где функция возрастает или убывает;
6)наибольшееи наименьшее значения функции, т.е. самое большое и самое маленькое значение зависимого переменного;
Свойства, которые имеют не все функции:
7) непрерывность;
8)ограниченность;
9) четность, нечетность;
10)вогнутость, выпуклость.
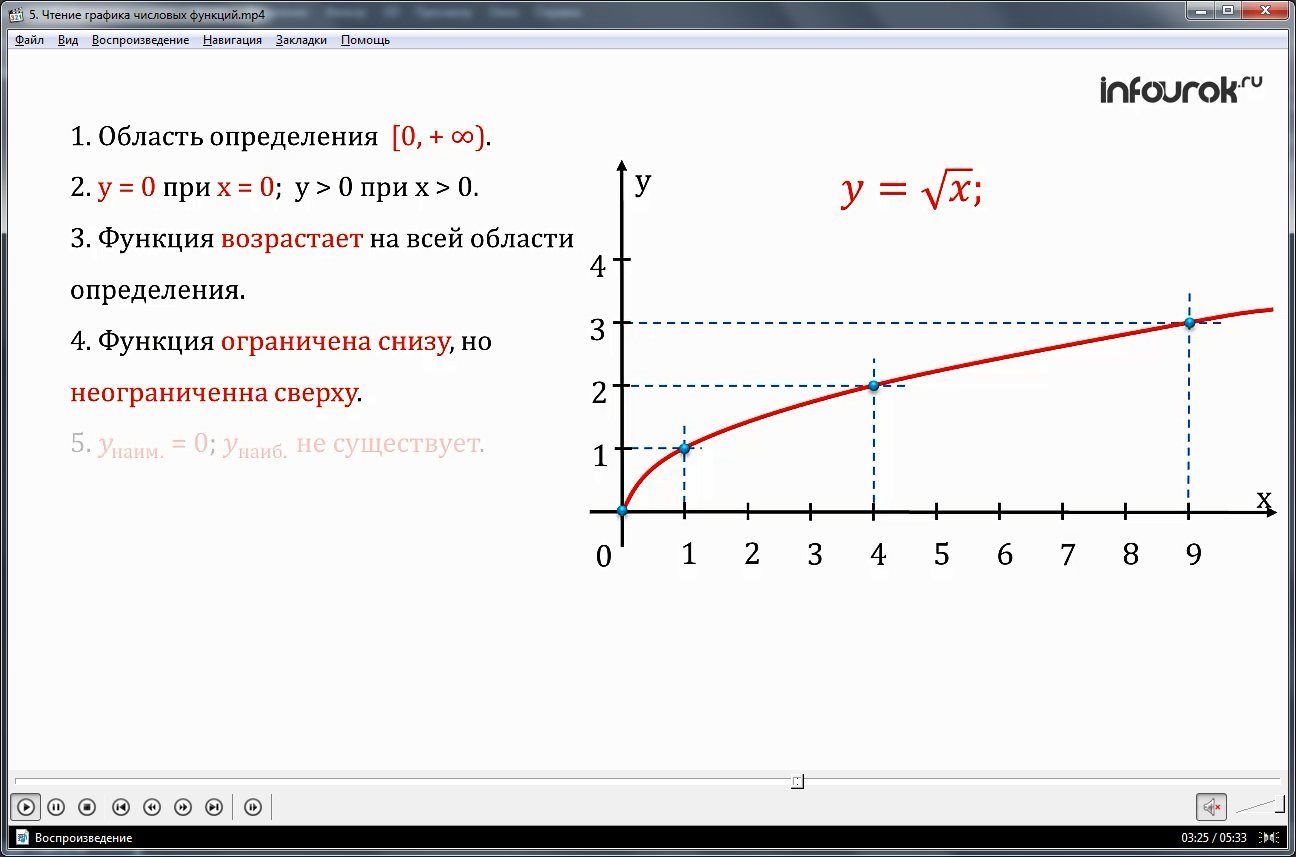
Прочитаем графики известных нам функций, например,игрек равен квадратный корень из икс.
1. Область определения функции —
луч от нуля до плюс бесконечности
2. Игрек равен нулю при икс равному нулю; игрек больше нуля при икс больше нуля.
3. Функция возрастает на всей области определения.
4. Функция ограничена снизу, но неограничена сверху .
5игрек наименьшее равное нулю достигается при икс равному нулю; игрек наибольшее не существует.
6.Функция непрерывна в заданной области определения.
7. Область значений функции — луч от нуля до плюс бесконечности
8.График обращен выпуклостью вверх.
у=кх+в

Прочитаем график ограниченной функции, график которой изображен
на рисунке 1.
1.Область определения функции – отрезок от минус трех до трех.
2.Функция имеет один нуль: икс равен нулю.
3.Положительные значения функция принимает при икс больше нуля и меньше или равно трем , отрицательные – при икс больше или равно минус трех и меньше нуля..
4.Она возрастающая, так как при икс первое меньше икс второевыполняется неравенство эф от икс первое меньше эф от икс второе .
5.Множество значений функции –отрезок от минус одного до одного.
6.Следовательно, наименьшее значение функции равно минус одному, а наибольшее – одному.
7.Функция ограничена и сверху и снизу.
8.На отрезке минус трех до нуля функция выпукла вниз, а
на отрезке нуля до трех выпукла вверх.
9.Непрерывна на всей области определения.
Сегодня, мы научились читать графики элементарных функций. На следующем уроке мы продолжим чтение графиков тригонометрических функций, показательной, логарифмической.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8015 |
| Номер материала | 828 |