
Урок "Как построить график функции у = f(kx), если известен график функции y = f(x)"

Краткое описание документа:
Материал, представленный в видеоуроке, является продолжением темы построения графиков функций путем различных преобразований. Мы рассмотрим, как строится график функции y=f(kx), если известен график функции у=f(x). В данном случае k – любое действительное число, не равное нулю.
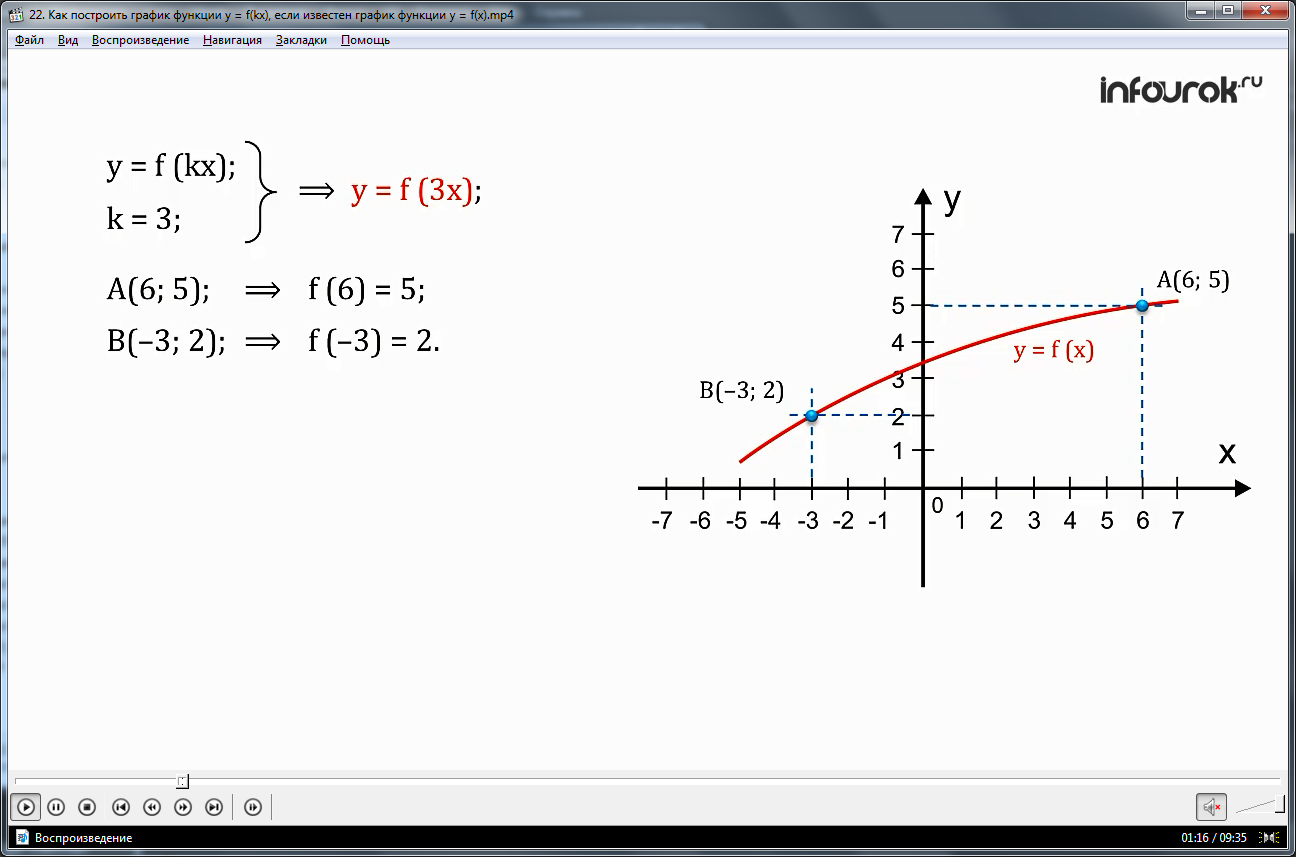
Вначале рассмотрим случай, когда k – положительное число. Для примера построим график функции у=f(3x), если график функции у=f(х) у нас есть. На рисунке на оси координат изображен график у=f(х), на котором есть точки с координатами А и В. Выбирая произвольные значения х и подставляя их в функцию у=f(3x), находят соответствующие значения функции у. Таким образом, получают точки графика функции у=f(3x)А1 и В1, у которых ординаты такие же, как у точек А и В. То есть мы можем сказать, что из графика функции у=f(x) путемсжатия с коэффициентом k к оси ординат можно получить график функции y=f(kx). Важно отметить, что точки пересечения с осью ординатпри сжатии остаются на прежнем месте.
В случае, когда k– отрицательное число, график функции y=f(kx) преобразовывается из графика функции у=f(x) путем растяжения от оси ординат с коэффициентом 1/k.
Автор приводит 1-й пример – построение графика функции у = sin 2x.
1) вначале строится часть волны графика функции у = sinх (см. рисунок);
2) т.к. k= 2, выполняется сжатие графика функции у= sinxк оси ординат, коэффициент сжатия равен 2. Находим точку пересечения с осью x. Т.к. график функции у = sinх пересекает ось абсцисс в точке π, то график функции у = sin 2х пересекает ось абсцисс в точке π/k = π/2.Аналогичным способом находятся все остальные точки графика функции у = sin 2xи по этим точкам строится весь график.
Рассмотрим 2-й пример – построение графика функции у =cos (x/2).
1) строим часть волны графика функции у = cosх (см. рисунок);
2) т.к. k =1/2, выполняем растяжение графика функции у = sinх от оси ординат с коэффициентом ½.
Найдем точку пересечения графика с осью х. Т.к. график функции у = cosх пересекает ось абсцисс в точке π/2, то график функции у =cos (x/2) пересекает ось абсцисс в точке π. Таким же образом находим все остальные точки графика функции у =cos (x/2), построим по этим точкам весь график.
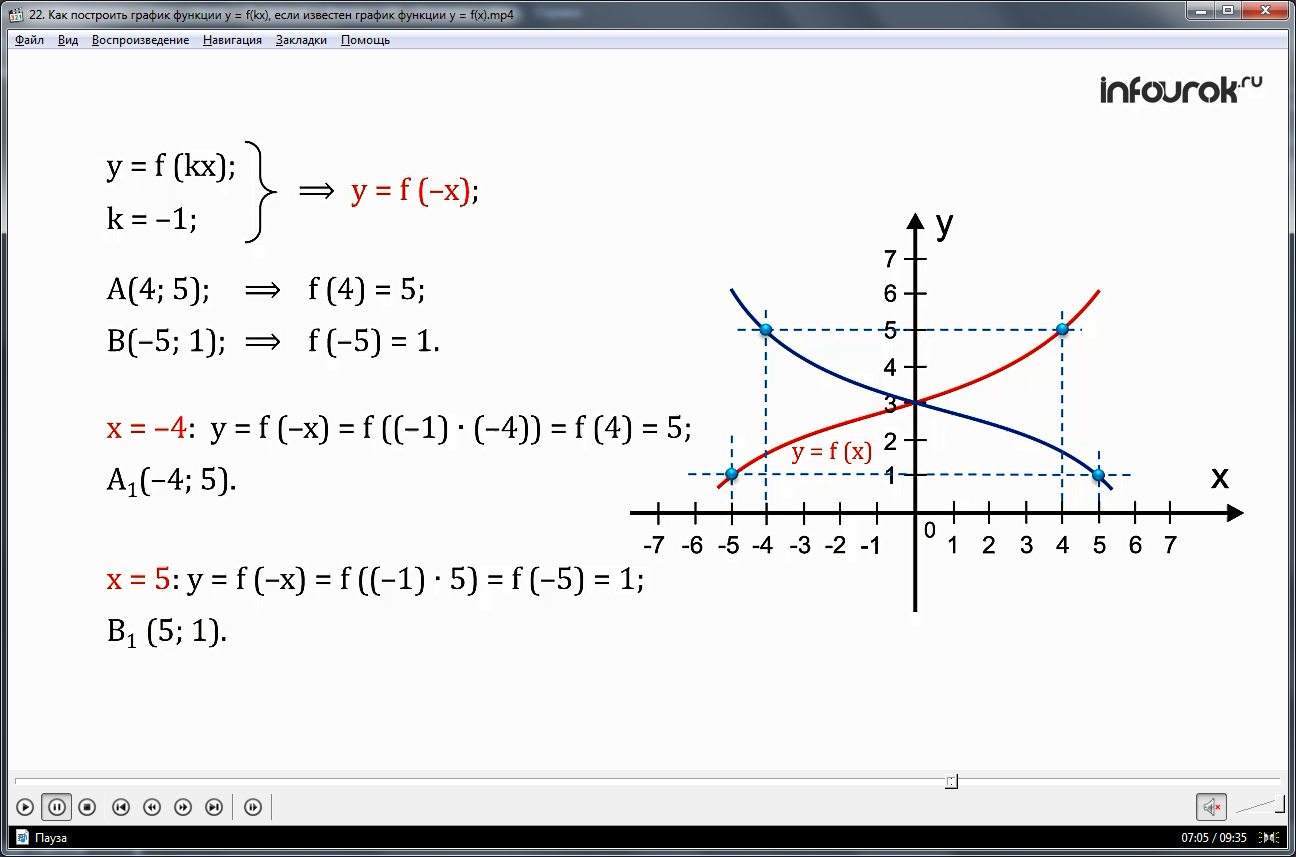
Далее рассмотрим вариант построения графика функции y=f(kx), где k - число отрицательное. Например, при k = –1 функция y=f(kx) = f(–x). На рисунке изображен график у=f(х), на котором есть точки с координатами А и В. Выбрав произвольные значения х и подставив их в функцию y=f(–x), находим соответствующие значения функции у. Получим точки графика функции y=f(–x)А1 и В1, которые будут симметричны точкам А и В относительно оси ординат. То есть при использовании симметрии относительно оси ординат из графика функции у=f(kx) получаем график функции y=f(–x).
Переходим к построению графика функции y=f(kx) при k<0 на примере функции у = 4 sin (- x/2).
1) построим часть волны графика у = sinх;
2) т.к. k= 4, выполним растяжение полуволны графика относительно оси абсцисс, где коэффициент растяжения равен 4;
3) выполним симметричное преобразование относительно оси абсцисс;
4) произведем растяжение от оси ординат (коэффициент растяжения равен 2);
5) завершим построение всего графика.
В данном видеоуроке мы подробно рассмотрели, каким образом поэтапно можно построить график функции y=f(kx) при разных значениях k.
ТЕКСТОВАЯ РАСШИФРОВКА:
Сегодня познакомимся с преобразованием, которое поможет научиться строить график функции у = f (kx)
( игрек равен эф от аргумента, который представляет произведение ка и икс), если известен график функции у = f (x) ( игрек равно эф от икс), где ка – любое действительное число (кроме нуля)».
1) Рассмотрим случай, когда k - положительное число на конкретном примере, когда k = 3.То есть нужно построить график функции
у = f (3x) ( игрек равен эф от трех икс), если известен график функции у = f (x). Пусть на графике функции у = f (x) есть точка А с координатами (6; 5) и В с координатами (-3; 2). Это значит, что f (6) = 5 и f (- 3) = 2 (эф от шести равно пяти и эф от минус трех равно двум). Проследим за перемещением этих точек при построении графика функции у = f (3x).
Возьмем произвольное значение х = 2, вычислим у, подставив значение х в график функции у = f (3x) , получим, что у = 5. (на экране: у = f (3x) = f (3∙2)= f (6) = 5.) То есть на графике функции у= f (3x) есть точка с А1 координатами (2; 5). Если же х = - 1, то подставив значение х в график функции у = f (3x), получим значение у= 2.
(На экране: у = f (3x) = f (- 1∙ 3) = f (- 3) = 2.)
То есть на графике функции у= f (3x) есть точка с координатами В1 (- 1; 2). Итак, на графике функции у = f (3x) есть точки с той же ординатой, что и на графике функции у = f (x), при этом абсцисса точки в два раза меньше по модулю.
То же будет справедливо и для других точек графика функции у = f (x), когда мы будем переходить к графику функции у = f (3x).
Обычно такое преобразование называют сжатием к оси у( игрек) с коэффициентом 3.
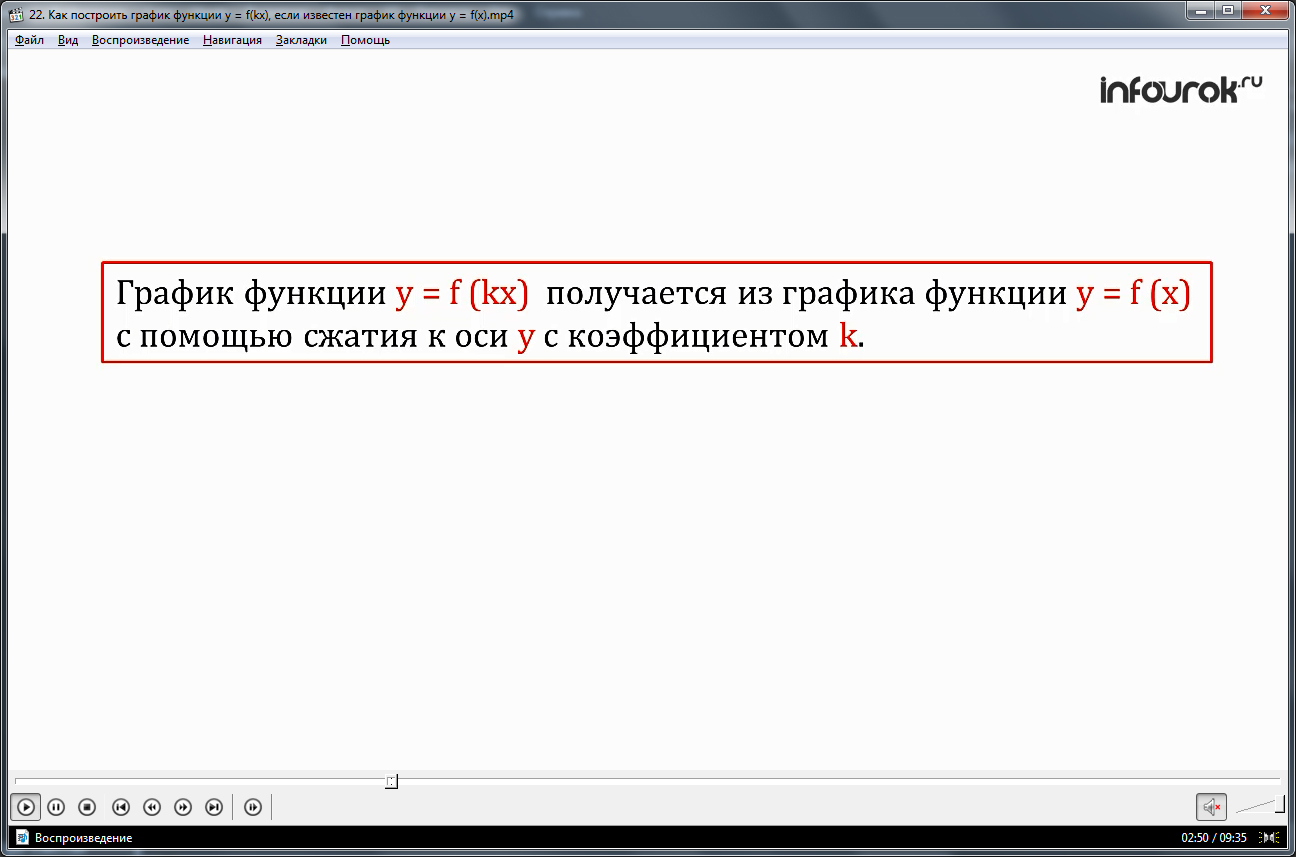
Следовательно, график функции у = f (kx) получается из графика функции у = f (x) с помощью сжатия к оси у(игрек) с коэффициентом k. Заметим, что при таком преобразовании на месте остается точка пересечения графика функции у = f (x) с осью ординат.
Если же k меньше единицы, то говорят не о сжатии с коэффициентом k, а о растяжении от оси у с коэффициентом ( то есть, если k = , то говорят о растяжении с коэффициентом 4).
ПРИМЕР 1. Построить график функции у = sin 2x ( игрек равен синусу двух икс).
Решение. Вначале построим полуволну графика у = sin x на промежутке от ноля до пи. Так как коэффициент равен двум, а значит k - положительное число больше единицы, значит осуществим сжатие графика функции у = sin x к оси ординат с коэффициентом 2. Найдем точку пересечения с осью ОХ. Если график функции у = sin x пересекает ось ОХ в точке π, то график функции у = sin 2x будет пересекать в точке (π: k =π: 2 = )(пи делим на ка равно пи деленное на два равно пи на два). Аналогичным способом найдем все остальные точки графика функции у = sin2 x. Так, точке графика функции у = sin x с координатами (;1) будет соответствовать точка графика функции у = sin 2x с координатами (;1). Таким образом получим одну полуволну графика функции у = sin 2x. Используя периодичность функции построим весь график.
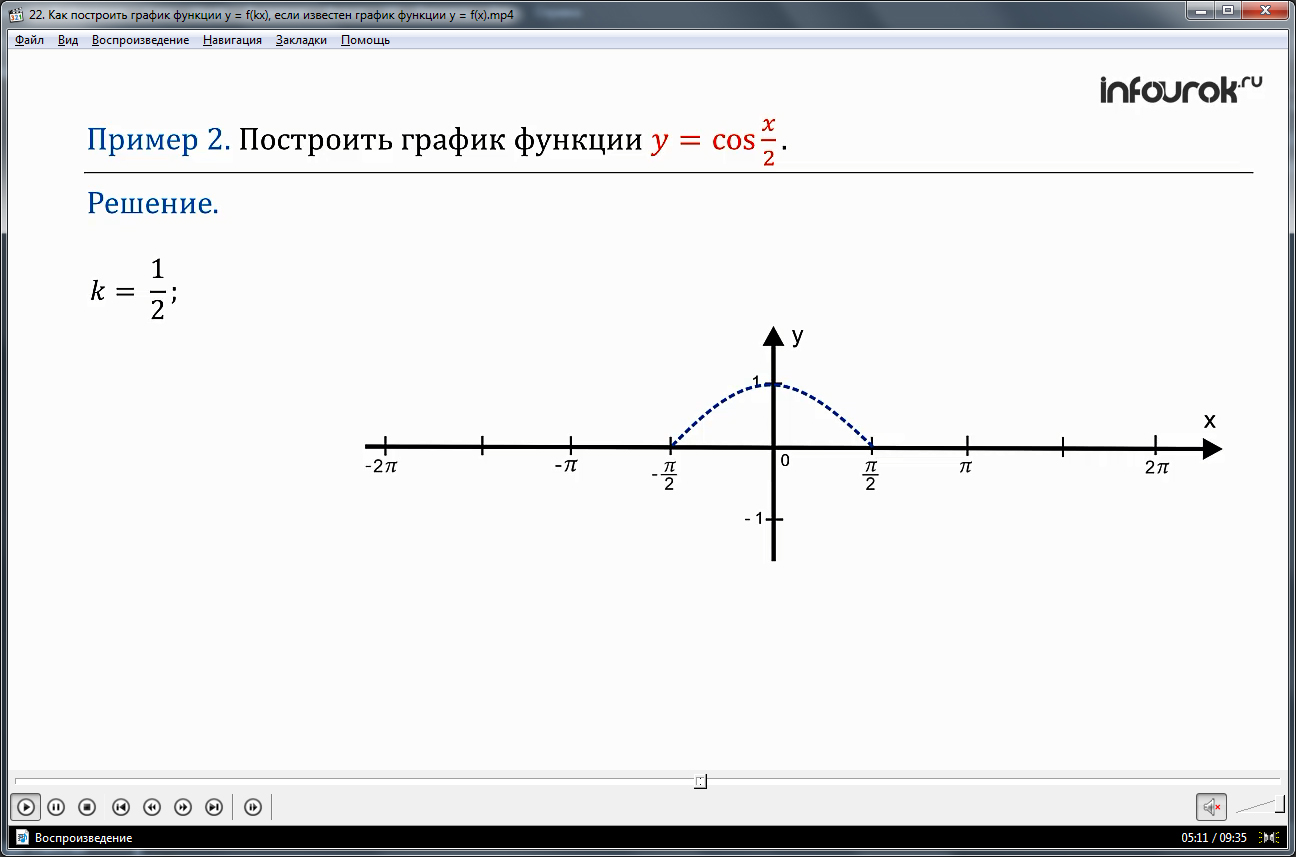
ПРИМЕР 2. Построить график функции у = cos ( игрек равен косинусу частного икс и двух ).
Решение. Вначале построим полуволну графика у = cos x. Так как k - положительное число меньше е единицы, значит осуществим растяжение графика функции у = cos x от оси ординат с коэффициентом 2.
Найдем точку пересечения с осью ОХ. Если график функции у = cos x пересекает ось ОХ в точке , то график функции у = cos будет пересекать в точке π. ( : k =π: = π ). Аналогичным способом найдем все остальные точки графика функции у = cos. Таким образом получим одну полуволну искомого графика функции. Используя периодичность функции построим весь график.
Рассмотрим случай, когда k равно минус единице. То есть нужно построить график функции у = f (-x) (игрек равен эф от минус икс), если известен график функции у = f (x). Пусть на графике есть точка А с координатами (4; 5) и точка В (-5; 1). Это значит, что f (4) = 5 и f (- 5) = 1.
Так как при подстановке в формулу у = f (-x) вместо х = - 4 получим у = f (4) = 5, то на графике функции у = f (-x) есть точка с координатами А1
( - 4 ; 5) (минус четыре, пять). Аналогично, графику функции у = f (-x) принадлежит точка В1 ( 5; 1).То есть графику функции у = f (x) принадлежат точки А(4; 5) и В(-5; 1), а графику функции у = f (-x) принадлежат точки А1 (- 4; 5) и В1 (5; 1). Эти пары точек симметричны относительно оси ординат.
Следовательно, график функции у = f (-x) с помощью преобразования симметрии относительно оси ординат можно получить из график функции у = f (x).
3) И, наконец, рассмотрим случай, когда k - отрицательное число. Учитывая, что равенство f (kx) = f (- |k|x) ( эф от произведения ка на икс равно эф от произведения минус модуля ка и икса) справедливое, то речь идет о построении графика функции у = f (- |k|x), который можно построить поэтапно:
1) построить график функции у = f (x);
2) построенный график подвергнуть сжатию или растяжению к оси ординат с коэффициентом |k| (модуль ка);
3) осуществить преобразование симметрии относительно оси у
( игрек) полученного во втором пункте графика.
ПРИМЕР 3. Построить график функции у = 4 sin (- ) (игрек равно четыре, умноженное на синус частного минус икс на два).
Решение. Прежде всего вспомним, что sin(- t) = -sint( синус от минус тэ равно минус синусу тэ), значит, у = 4 sin (- ) = - 4 sin (игрек равен минус четырем, умноженным на синус частного икс на два). Строить будем поэтапно:
1) Построим одну полуволну графика функции у= sinх.
2) Осуществим растяжение построенного графика от оси абсцисс с коэффициентом 4 и получим одну полуволну графика функции
у= 4sinх( игрек равно четыре, умноженное на синус икс).
3) К построенной полуволне графика функции у= 4sinх применим преобразование симметрии относительно оси х( икс) и получим полуволну графика функции у= - 4sinх.
4) Для полуволны графика функции у= - 4sinх осуществим растяжение от оси ординат с коэффициентом 2; получим полуволну графика функции - 4 sin .
5) С помощью полученной полуволны построим весь график.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11542 |
| Номер материала | 850 |