
Урок "Конус"

Краткое описание документа:
Видеоурок «Конус» раскрывает понятие этой фигуры как тела вращения, описывает элементы конуса, демонстрирует выведение формулы определения площади конической поверхности. Задача видеоурока – сформировать представление о конусе с точки зрения стереометрии, способствовать запоминанию и усвоению учебного материала по данной теме. Материал может быть использован как самостоятельная часть урока, заменяя объяснение учителя по новой теме, а также может служить наглядным пособием при представлении учителем новой темы урока.
Использование в видеоуроке специальных приемов для повышения эффективности обучения дает возможность обеспечить более глубокое понимание предмета и запоминание учебного материала. Сам видеоурок является средством, вносящим разнообразие в урок, и акцентирующим внимание учеников на изучаемом предмете. Анимационные эффекты помогают представить материал в виде, наиболее удобном для усвоения. Определения, понятия и важные детали построений выделяются цветом для лучшего запоминания. Видео дополнено важными голосовыми комментариями, иллюстрациями.
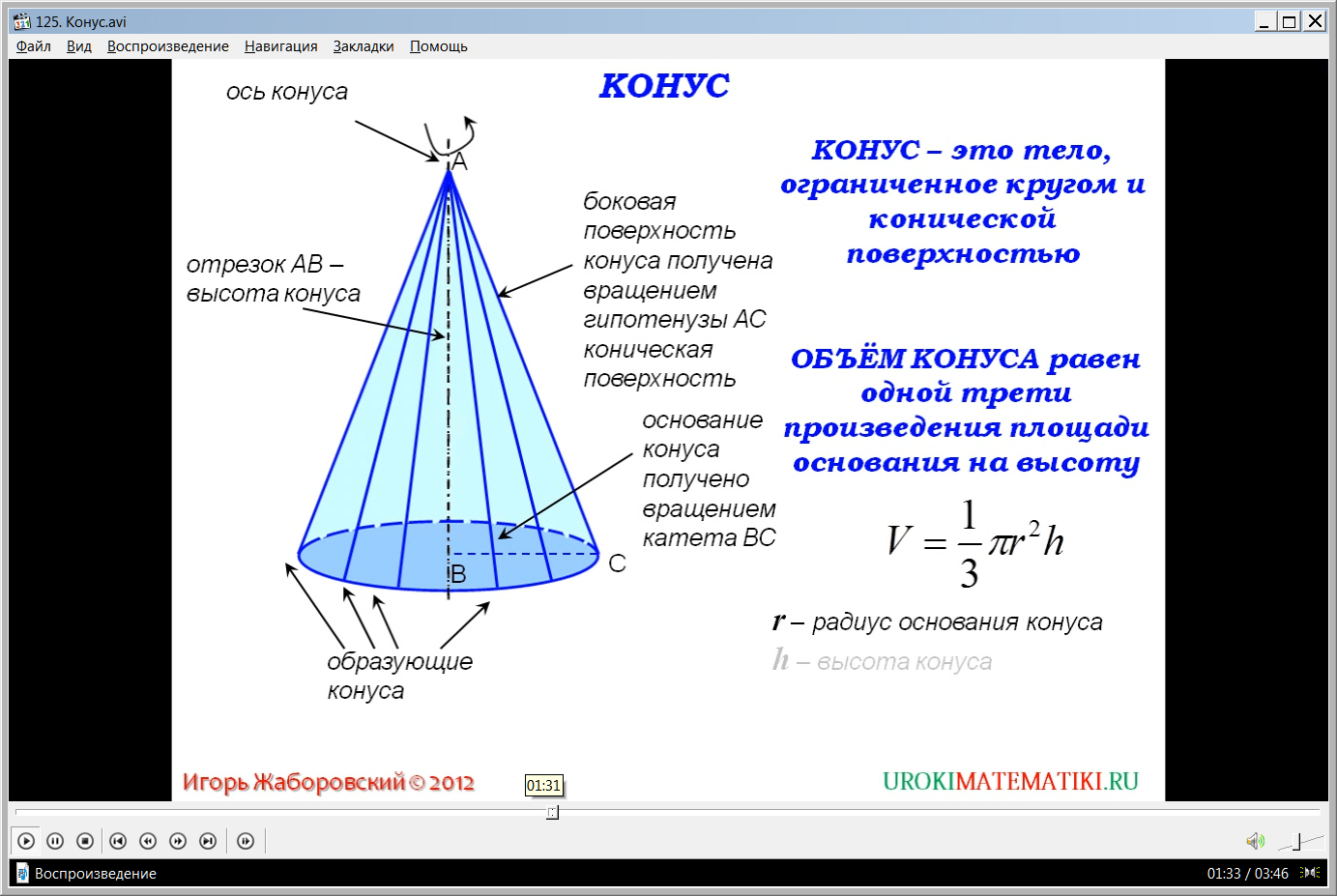
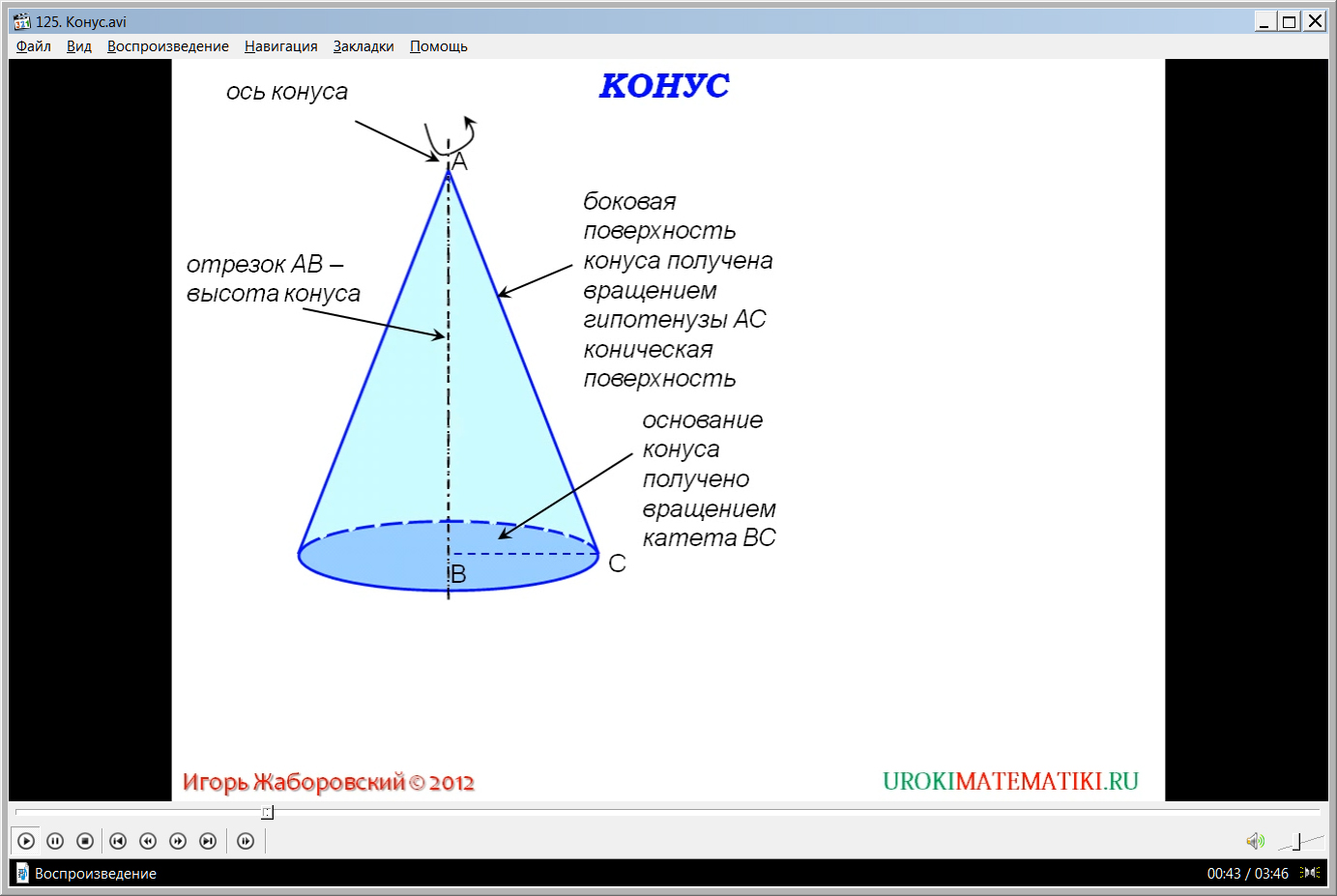
Видеоурок начинается с представления названия темы. Раскрывается механизм образования конуса как тела вращения некоторого прямоугольного треугольника вокруг катета. На рисунке изображен прямоугольный треугольник АВС, который вращается вокруг стороны АВ. В результате вращения получается фигура, называемая конусом. Отмечается, что прямая, содержащая сторону АВ, вокруг которой вращался треугольник, является осью конуса, а высоту конуса представляет отрезок АВ. Второй катет ВС треугольника ΔАВС при вращении образует круг, радиус которого равен ВС. Этот круг - основание конуса. В результате вращения гипотенузы данного треугольника образуется поверхность, составленная из отрезков, имеющих общий конец А. Иначе данная поверхность называется конической или боковой поверхностью конуса. Составляющие ее отрезки называются образующими. Таким образом выводится определение конуса как геометрического тела, ограниченного некоторым кругом вместе с конической поверхностью.
Также отмечается, что объем конуса можно определить по формуле, представляющей собой треть произведения его площади основания с высотой. Представлена формула для вычисления V=(1/3)πr2h. В формуле r является радиусом основания конуса, а h – его высотой. Справедливость данной формулы для нахождения объема доказывается с использованием принципа Кавальери.
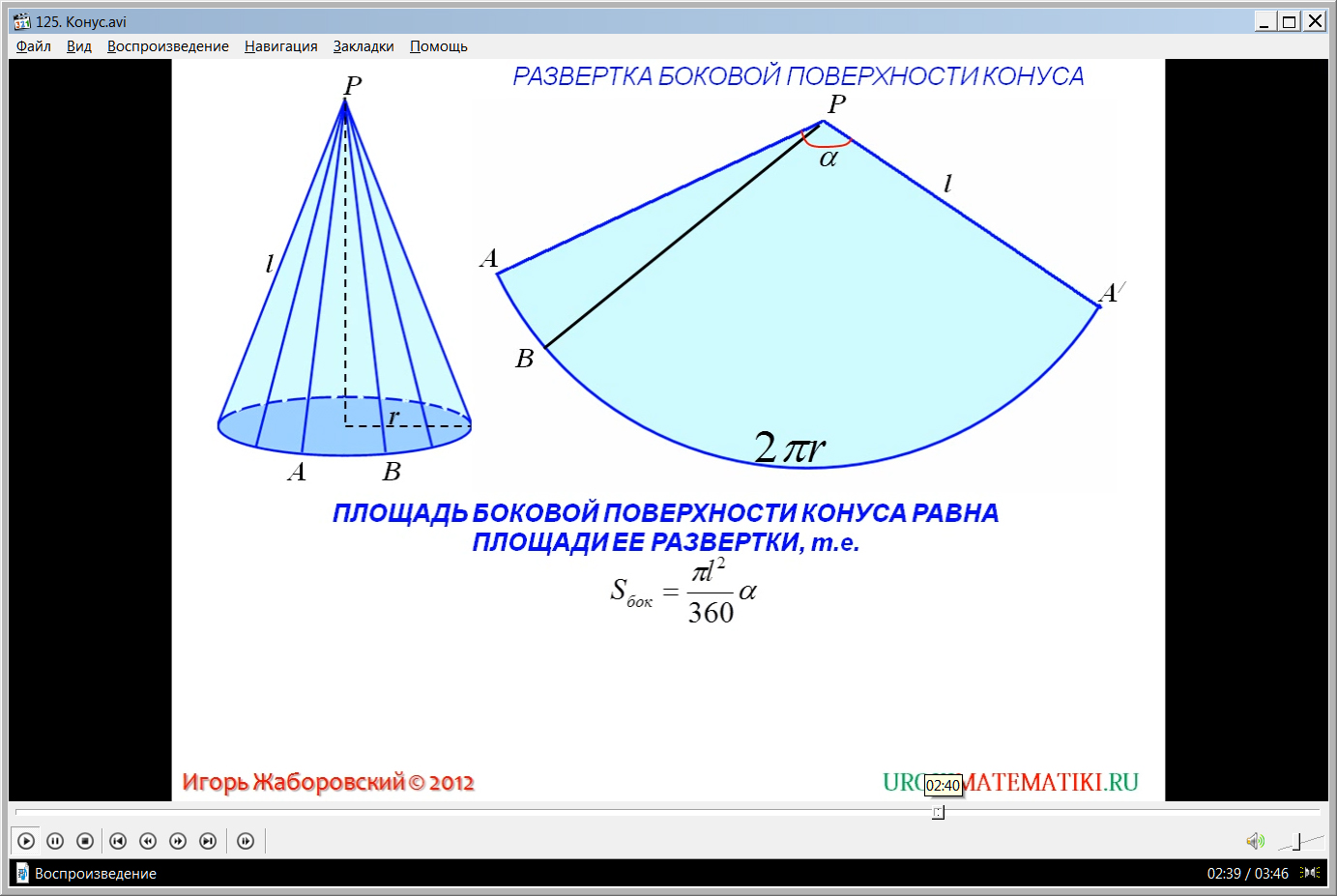
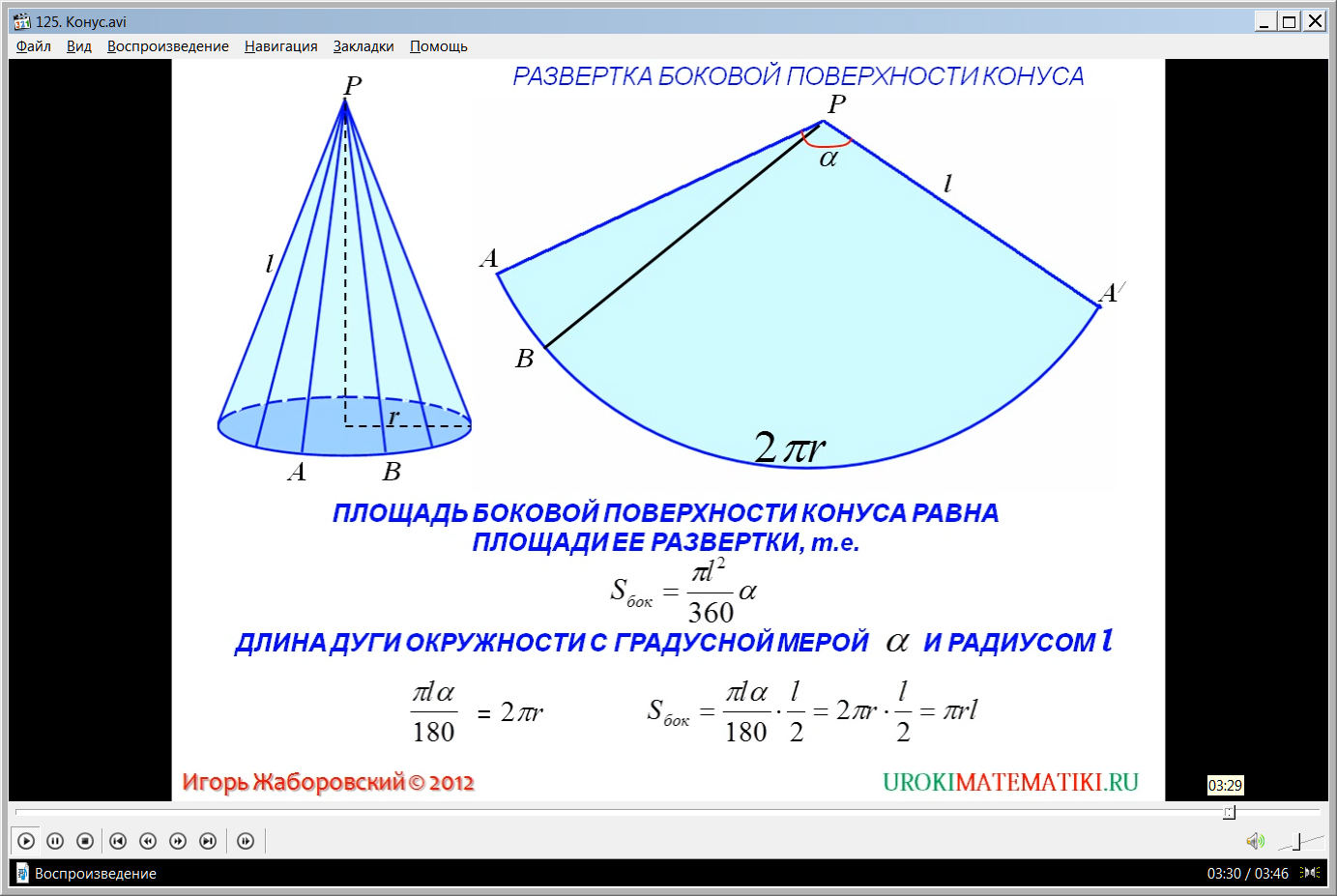
Далее рассматривается вывод формулы для нахождения площади боковой поверхности. На рисунке изображается конус с радиусом основания r, высотой конуса h. Рядом располагается развернутая боковая поверхность конуса, разрезанная по некоторой его образующей. Очевидно, что данная развертка представляет собой круговой сектор. Радиусом сектора является образующая l. При этом длина дуги представляет собой длину окружности основания конуса. Используя формулу для нахождения площади кругового сектора, при подстановке соответствующих элементов из данной фигуры получаем формулу нахождения площади конической поверхности – S=πl2*α/360 с учетом того, что α – это угол кругового сектора. А длина дуги окружности сектора круга радиусом rс градусной мерой α определяется по формуле πlα/180. Также длину дуги можно определить через радиус основания 2πR. Это значит, что между данными выражениями можно поставить знак равенства πlα/180=2πR. Соответственно, площадь боковой поверхности можно определить по формуле S=(πlα/180)*(l/2). После преобразования данной формулы и сокращения получаем окончательную формулу для нахождения площади боковой поверхности S=πrl.
Видеоурок «Конус» может применяться на традиционном уроке геометрии в школе для повышения эффективности обучения. Также данный материал может послужить инструментом обучения в ходе дистанционного обучения. Учитель может рекомендовать освоение темы с использованием данного материала ученикам, требующим дополнительных занятий для более глубокого понимания предмета.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6327 |
| Номер материала | 735 |