
Урок "Координаты вектора"

Краткое описание документа:
Видеоурок «Координаты вектора» демонстрирует видеоматериал, который помогает учителю объяснить ученикам данную тему. В состав видеоурока входит подробное объяснение понятия координатного вектора, рассматриваются свойства координатных векторов. Задача данного видеоурока – облегчить понимание учебного материала, запоминание основных свойств векторов, их доказательства. Данное видео может заменить объяснение учителя и освободить его время для индивидуальной работы, или служить сопровождением объяснению учителя.
Представление материала в виде видеоурока дает возможность при помощи анимации, иллюстраций, голосового сопровождения использовать все инструменты влияния для глубокого понимания и усвоения материала. Он структурирован, хорошо виден всем ученикам, наглядно демонстрирует особенности построений.
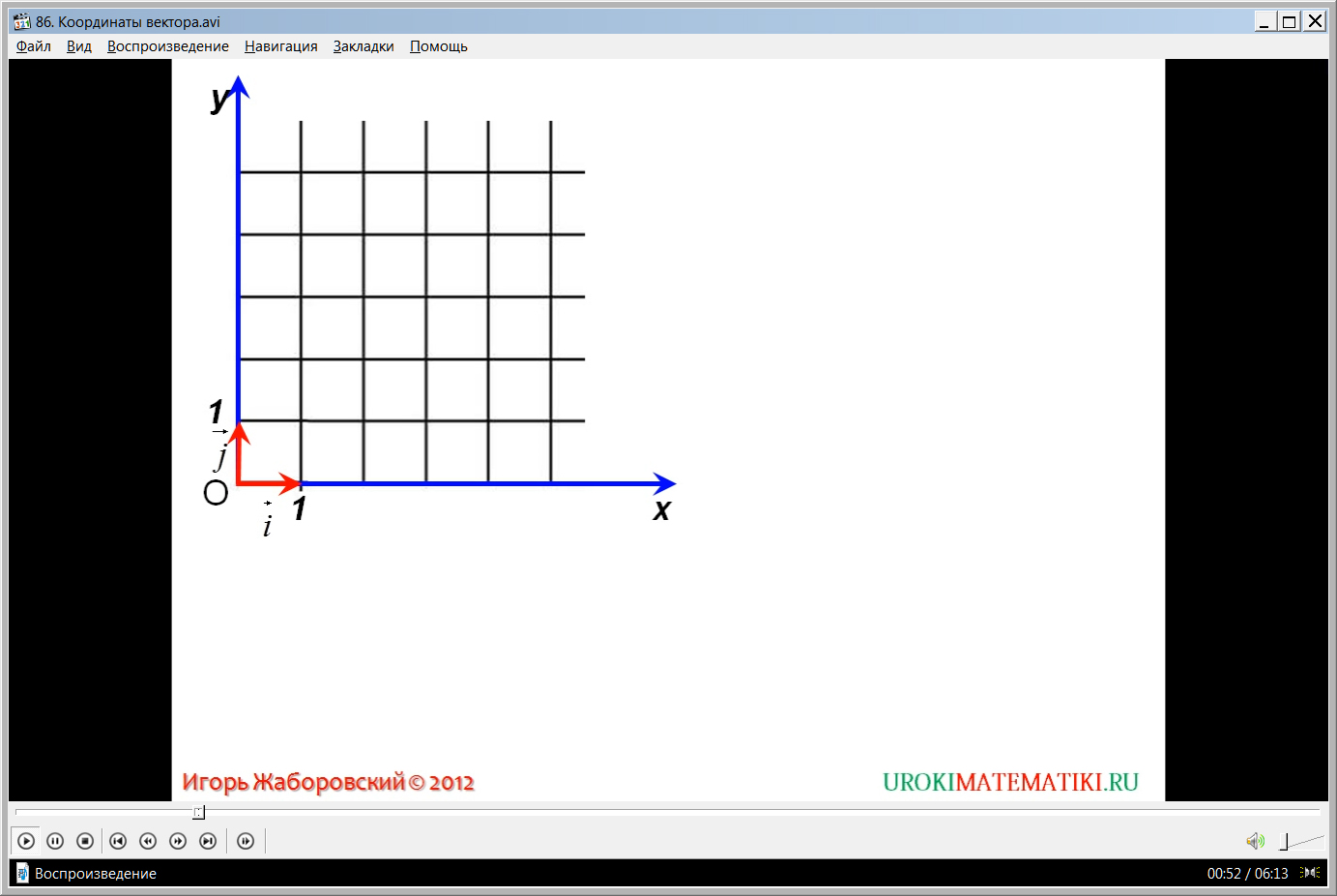
Вначале урока после представления темы ученикам напоминается ранее изученный материал о прямоугольной системе координат. Параллельно объяснению на экране демонстрируется построение прямоугольной системы координат ХОУ. Напоминается, что прямоугольная система координат строится на основе построения двух взаимно перпендикулярных прямых, каждой из которых придается направление, отмеченной стрелкой на рисунке. Затем выбирается единичный отрезок на каждой прямой. Он отмечается положительным числом и далее длина отрезка выражается данным числом.
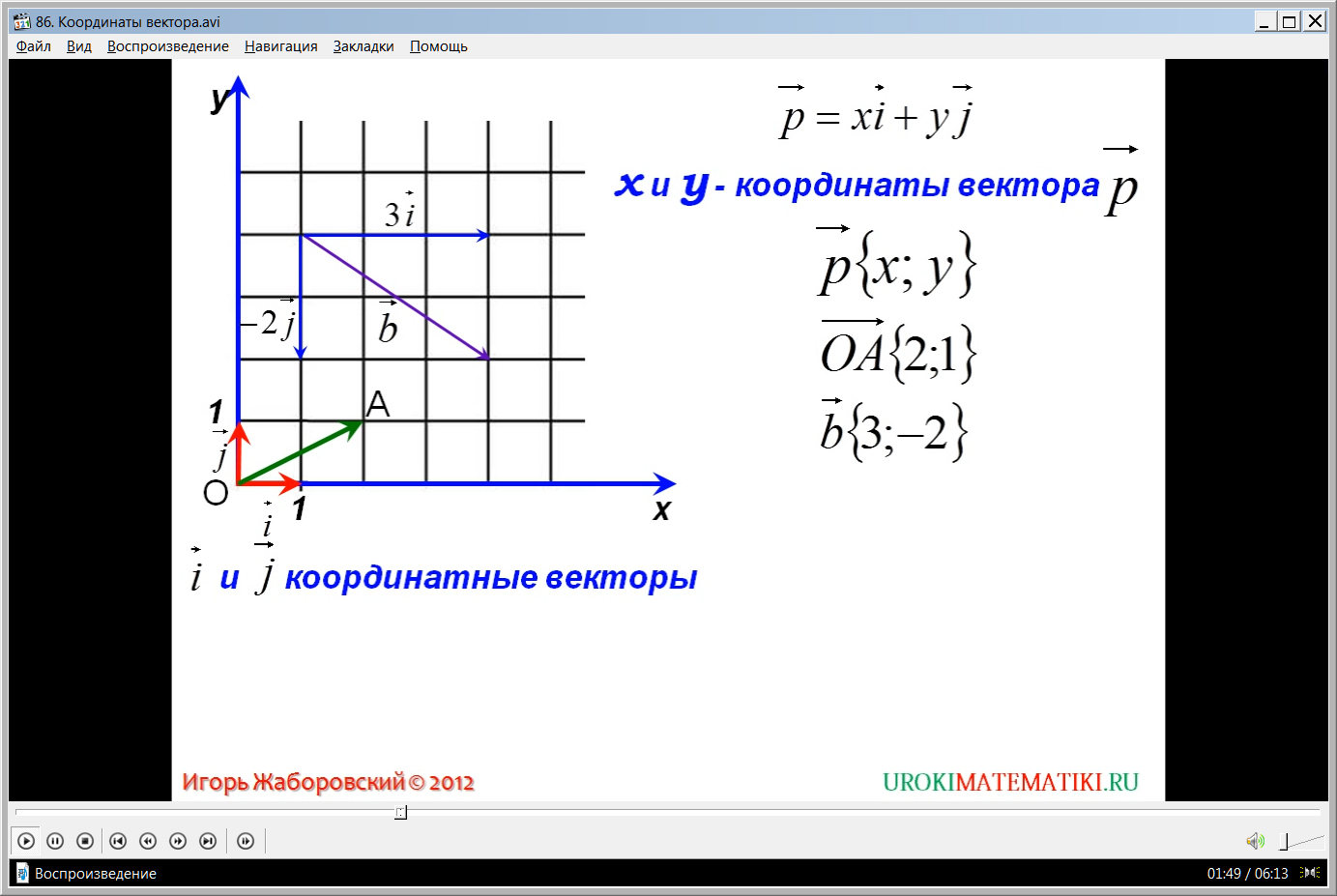
Далее на построенной координатной плоскости демонстрируется построение единичных векторов iˉ и gˉ, длина которых равна единичному отрезку, а направления совпадают с направлением осей х и у. Данные векторы называются координатными, что отмечено на экране и выделено цветом. Отмечается, что данные векторы неколлинеарны, поэтому по ним раскладывается любой вектор. Это разложение можно представить в виде рˉ = хiˉ + уjˉ, где числа х и у являются координатами вектора рˉ в построенной системе координат. Ученикам предлагается запомнить обозначение координат вектора рˉ{х;у}, выведенное на экран.
Для усвоения изученных понятий приводятся примеры векторов и их координат: вектор ОАˉ{2;1}, bˉ{3;-2}. На координатной плоскости определение координат вектора подкрепляется построением соответствующих векторов, образующих координаты данного вектора. Рассматривается нулевой вектор 0ˉ{0;0}, разложение которого представлено в виде 0ˉ= 0·iˉ + 0·jˉ. А также рассматриваются свойства равных векторов aˉ и bˉ. На экране продемонстрировано, каким образом доказывается. Что соответствующие координаты равных векторов равны: из равенства aˉ= х1iˉ + у1jˉ= bˉ= х2iˉ + у2jˉ следует х1=х2, у1=у2.
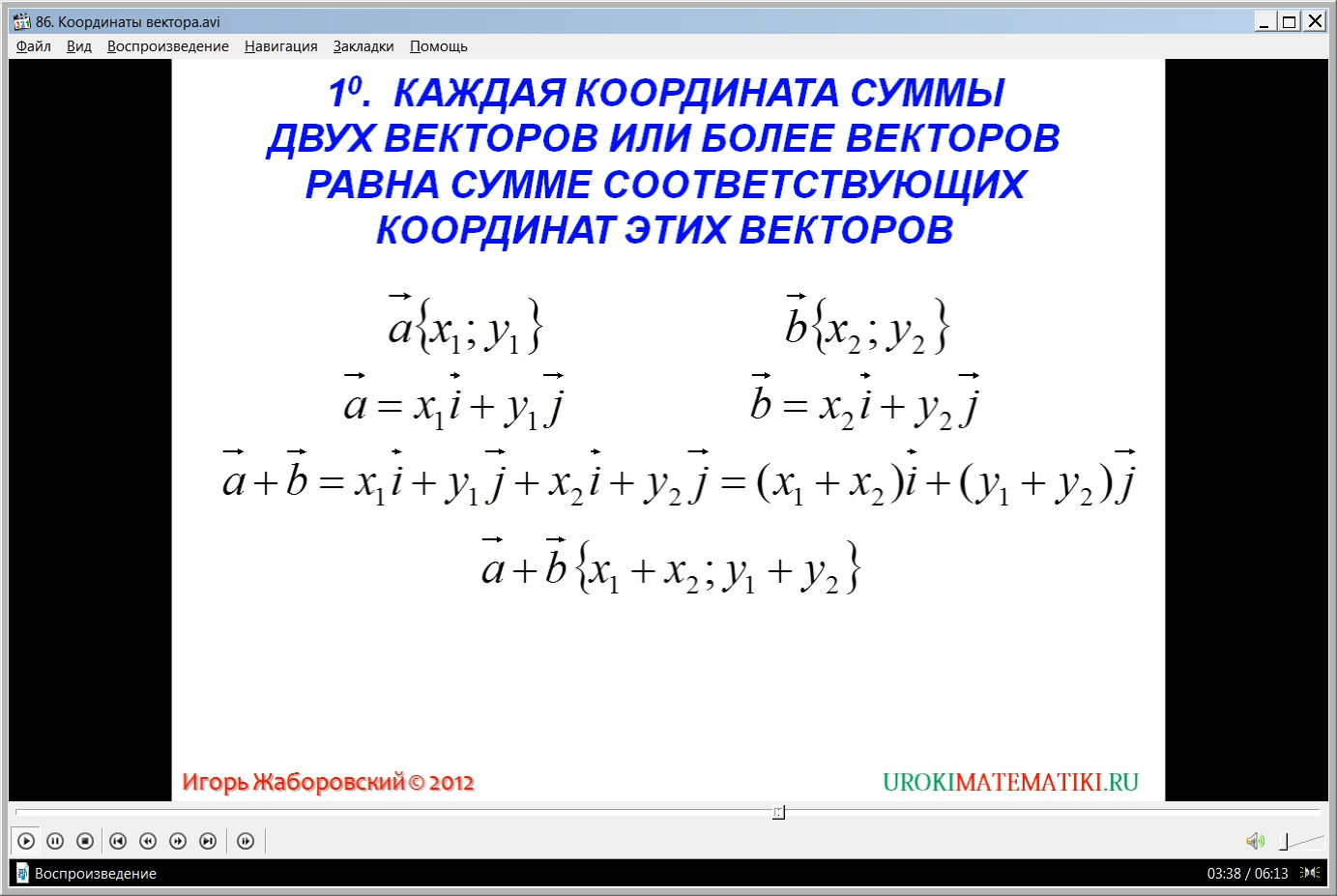
В ходе видеоурока рассматриваются правила, согласно которым определяются координаты вектора суммы двух векторов, разности, произведения вектора на некоторое число.
На экране демонстрируется первое правило, которое утверждает, что каждая координата суммы векторов будет равна сумме соответствующих векторов складываемых векторов. Для доказательства утверждения на экране представлены два вектора с координатами aˉ{х1;у1} и bˉ{х2;у2}. Данные векторы представляются разложенными по координатным векторам aˉ= х1iˉ + у1jˉ и bˉ= х2iˉ + у2jˉ. Пользуясь правилом сложения векторов, получаем выражение для сложения aˉ+bˉ= х1iˉ + у1jˉ+х2iˉ + у2jˉ. После вынесения общего множителя за скобки, получаем разложение по координатным векторам суммарного вектора (х1+ х2)iˉ+(у1+ у2)jˉ. Данное разложение свидетельствует о том, что координаты суммарного вектора равны aˉ+bˉ{(х1+ х2); (у1+ у2)}.
Демонстрация второго правила аналогична первому. На экране формулируется данное правило. Оно утверждает, что каждая из координат вектора разности двух векторов равна разности каждого из координат этих векторов. Подтверждение правило производится также аналогично первому. Есть два вектора с некоторыми координатами aˉ{х1;у1} и bˉ{х2;у2} и разложением по векторам aˉ= х1iˉ + у1jˉ и bˉ= х2iˉ + у2jˉ. Для нахождения их разности из разложения по векторам первого вектора вычитается разложение по векторам второго вектора aˉ-bˉ= х1iˉ + у1jˉ-х2iˉ - у2jˉ. После перегруппировки в выражении получим, что разложение разностного вектора (х1- х2)iˉ+(у1- у2)jˉ. Поэтому можно утверждать, что разностный вектор будет иметь координаты, которые представляют собой разности соответствующих координат исходных векторов aˉ-bˉ{(х1- х2); (у1- у2)}.
Демонстрируется формулировка третьего правила, утверждающего, что при умножении вектора на число каждая координата данного вектора умножается на это число. Справедливость правила подтверждается в результате простых преобразований. Есть некоторый вектор aˉ{х;у}. При умножении его на число k получим вектор kaˉ. Разложение вектора по координатным векторам aˉ= хiˉ + уjˉ. Соответствующее ему разложение по координатным векторам вектора kaˉ= kхiˉ + kуjˉ. Значит, координатами такого вектора будут kaˉ{kх; kу}. Отмечается, что подобным образом могут быть определены координаты любого вектора, представленного в виде алгебраической суммы двух координатных векторов.
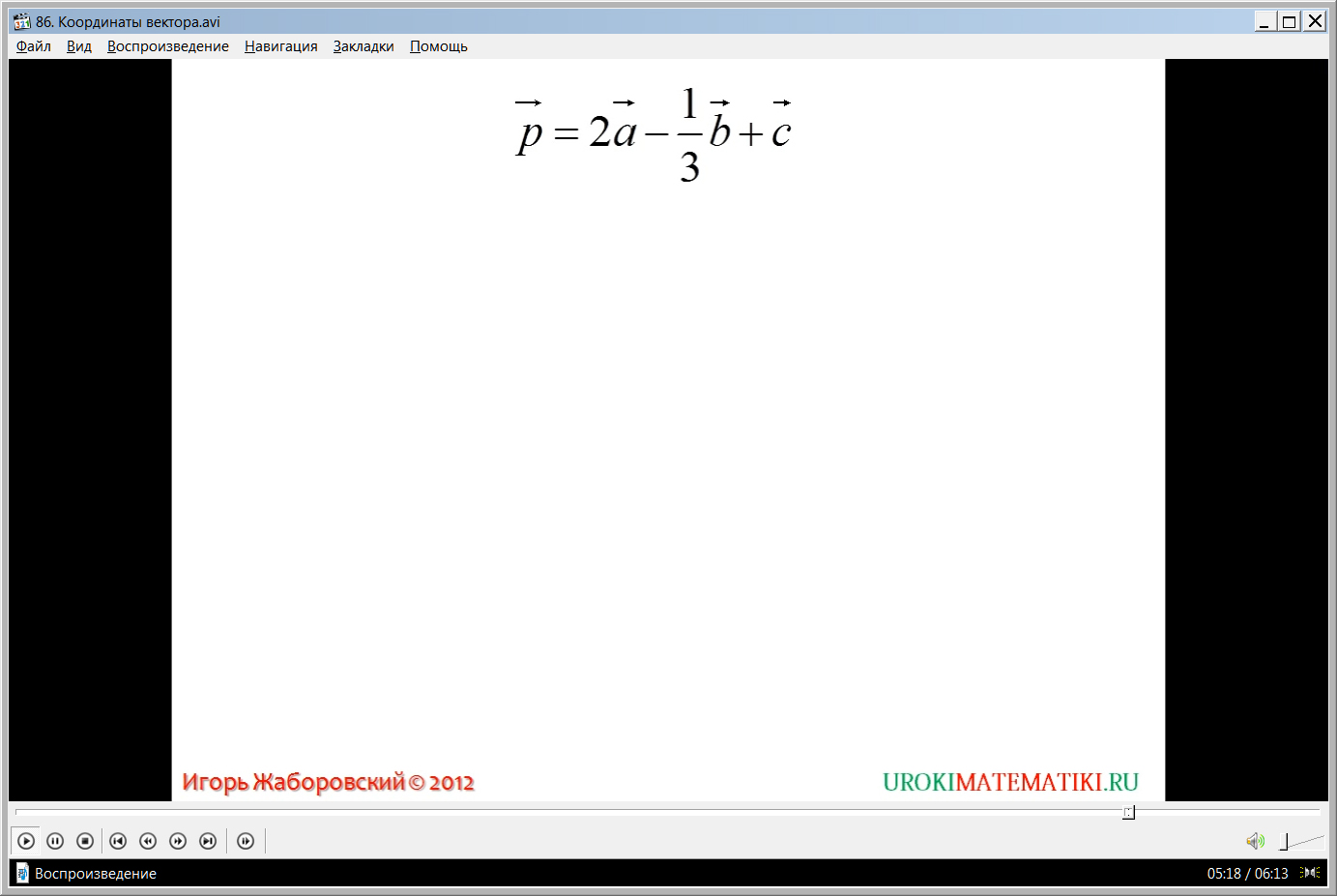
Для усвоения изученного материала рассматривается пример, где необходимо найти координаты вектора рˉ=2aˉ-(1/3)bˉ+сˉ. Даются координаты входящих в алгебраическую сумму векторов aˉ{1;-2}, bˉ{0;3}, сˉ{-2;3}. Для решения необходимо найти значения соответствующих выражений 2aˉ и -(1/3)bˉ. Применяя третье правило, обнаруживаем, что координаты данных векторов 2aˉ{2;-4} и -(1/3)bˉ{0;-1}. Применяя первое правило для нахождения суммы векторов, определяем их координаты, складывая соответствующие координаты векторов, входящих в сумму: {2+0-2;-4-1+3}. После сложения, получаем рˉ{0;-2}.
Видеоурок «Координаты вектора» предназначен для использования учителем математики в школе. Также он может послужить наглядным пособием в ходе дистанционного обучения, помочь понять и запомнить материал ученику при самостоятельном изучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8378 |
| Номер материала | 774 |