
Урок "Квадрат суммы нескольких слагаемых"

Краткое описание документа:
Стандартные формулы сокращенного умножения рассчитаны на работу с биномами и относительно простыми (по базовой конструкции) многочленами. Однако иногда при решении более серьезных задач приходится иметь дело с более сложными операциями.
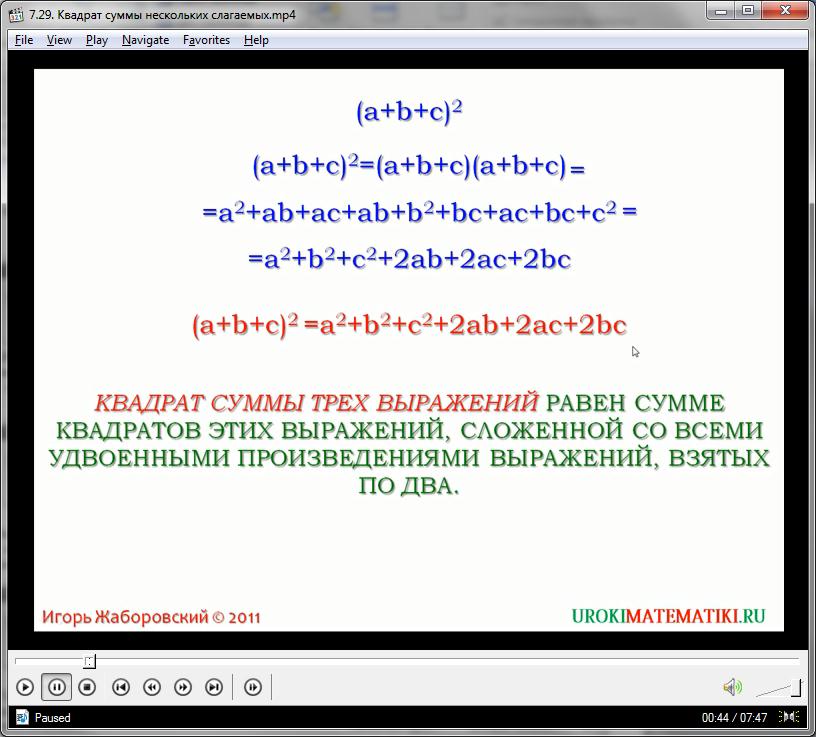
В данном видеоуроке мы изучим процесс возведения в квадрат целого трехчлена. Для этого, сразу же выведем готовую формулу, используя абстрактный пример и принимая во внимание правила перекрестного почленного перемножения любых многочленов:
(а + b + с)2 = (а + b + с)(а + b + с) =
= а2 + аb + ас + аb + b2 + bс + ас + bс + с2 =
= а2 + b2 + с2 + 2аb + 2ас + 2bс
Таким образом, при помощи данного видео мы эмпирическим путем вывели готовую формулу, которую можно выразить на словах следующим законом: квадрат суммы трех натуральных выражений равен сумме квадратов этих выражений, сложенной с суммой всех удвоенных произведений выражений, взятых в паре.
Для практики изучим новую формулу на упражнении. Вычислить значение квадрата:
(2а + х + 3с)2
Используя вышеуказанное равенство, получаем новое выражение и раскрываем скобки:
(2а + х + 3с)2 = (2а)2 + х2 + (3с)2 + 2(2ах) + 2(2а3с) + 2(х3с) =
= 4а2 + х2 + 9с2 + 4ах + 12ас + 6сх
Как видим, применение формулы для возведения в квадрат суммы трех выражений достаточно простой процесс, требующий лишь внимания, особенно при перемножении коэффициентов.
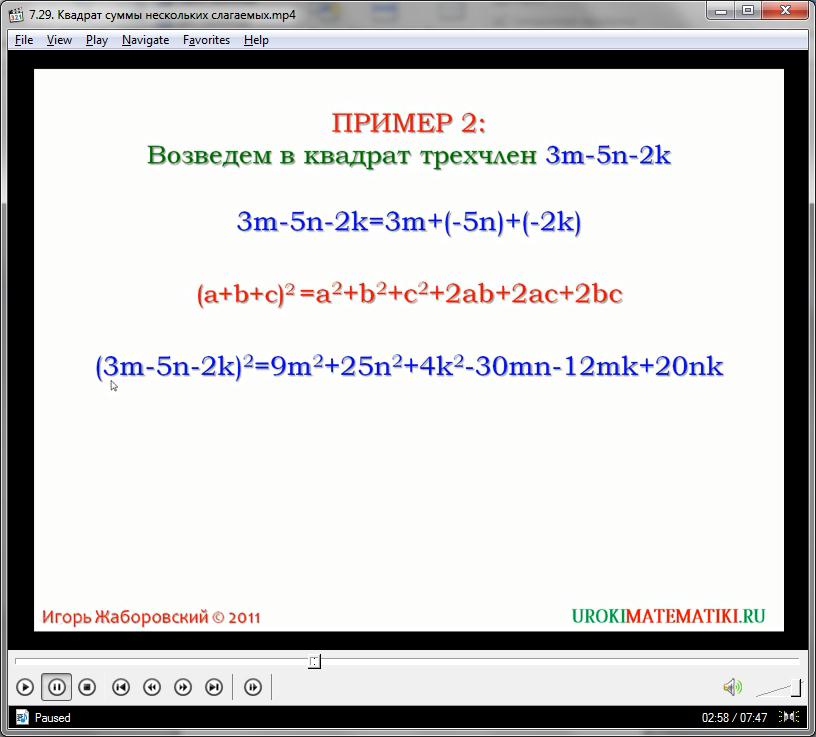
Так как сумма в скобках формулы имеет алгебраический смысл, то данное равенство успешно можно применять и для разности выражений – фактически, для любого трехчлена. Для нового упражнения инверсируем знаки в нашем первом примере:
(2а – х – 3с)2
Чтобы решить это выражение при помощи формулы для квадрата суммы, воспользуемся отделением знаков коэффициентов в скобки, то есть запишем трехчлен в виде алгебраического суммирования:
(2а – х – 3с)2 = (2а +(– х) + (– 3с))2
Как мы помним из предыдущих видеоупражнений, вынесение плюса за скобки ни на что не влияет, так как плюс сохраняет первичные знаки выражений. Пользуясь формулой, произведем вычисления:
(2а +(– х) + (– 3с))2 = (2а +(– х) + (– 3с))(2а +(– х) + (– 3с)) =
= (2а)2 + (-х)2 + (-3с)2 + 2(-2ах) + 2(-2а3с) + 2(3сх) =
= 4а2 + х + 9с2 – 4ах – 12ас + 6сх
Если внимательно присмотреться к ответу, можно сделать следующий вывод: разность в начальном выражении привела к тому, что два из трех удвоенных произведений пар выражений приобрели знак «минус». Все остальные данные остались прежними. Стоит заметить, что квадрат всего аннулирует минус, поэтому первая часть суммы в ответе не будет зависеть от знаков в начальном выражении и всегда остается положительной.
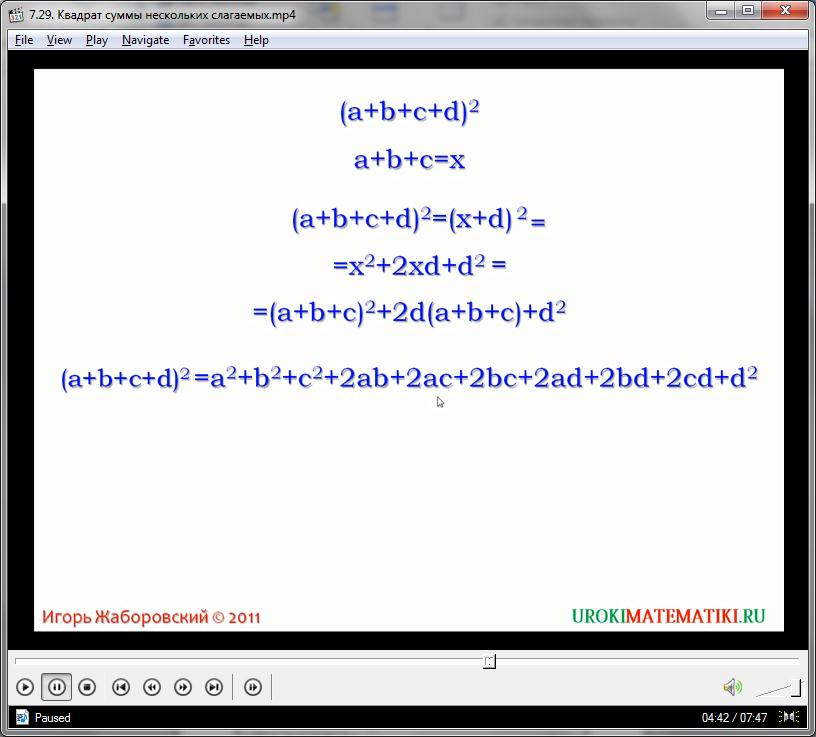
Усложним задачу и попытаемся вычислить квадрат суммы четырех выражений. При этом воспользуемся стандартными ФСУ для облегчения расчетов:
(а + х + у + с)2 = ((а + х + у) + с)2 =
= (а + х + у)2 + 2(а + х + у)с + с2
= а2 + х2 + у2 + 2ах + 2ау + 2ху + 2ас + 2хс + 2ус + с2 =
= а2 + х2 + у2 + с2 + 2ах + 2ау + 2ас + 2ху + 2хс + 2ус
Конечное выражение является формулой для определения квадрата суммы четырех выражений. Или в словесном виде: квадрат суммы четырех натуральных выражений равен сумме квадратов этих выражений, сложенной с удвоенными произведениями всех выражений, взятых по паре.
Таким образом, возведение в квадрат любого многочлена является довольно стандартизованным и приводит к подобным результатам, поэтому можно вывести общую формулировку, работающую для любого конечного числа выражений:
квадрат суммы нескольких выражений равен сумме квадратов данных выражений, сложенных с удвоенными произведениями всех выражений, взятых по паре.
Рассмотрим следующую задачу. Возведем в квадрат выражение:
(3 + х – 5у + 3с)2
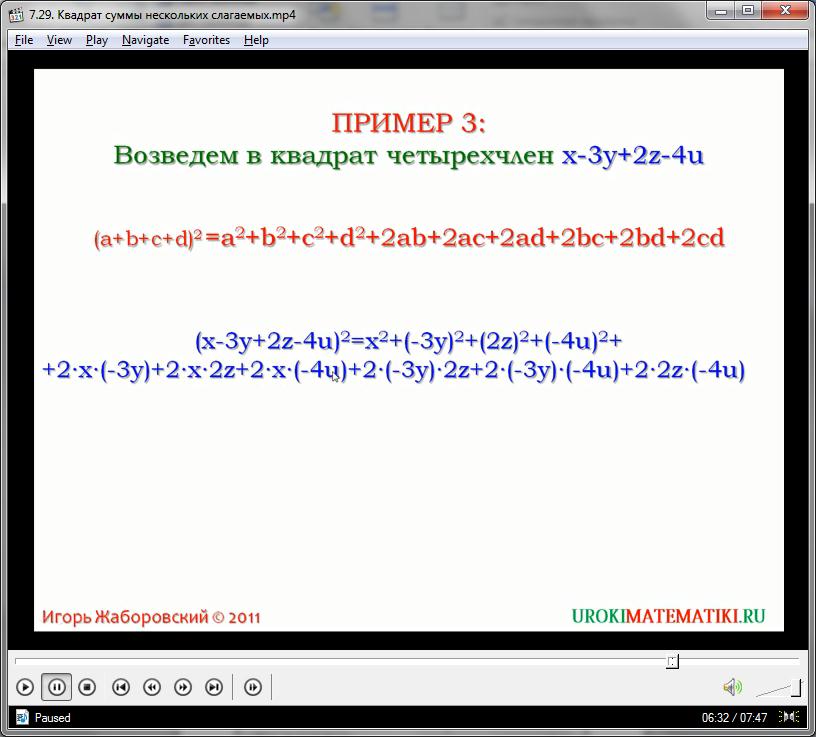
Используя выведенные формулы или общую формулировку (работающую для любой алгебраической суммы), преобразуем и решим, раскрывая скобки и упрощая:
(3 + х – 5у + 3с)2 = (3 + х + (– 5у) + 3с)2 =
= (3 + х + (– 5у) + 3с)(3 + х + (– 5у) + 3с) =
= (3)2 + х2 + (-5у)2 + (3с)2 + 2(3х) + 2(-15у) + 2(9с) + 2(-5ух) + 2(3сх) – 30ус
= 9 + х2 + 25у2 + 9с2 + 6х – 30у + 18с – 10ух + 6сх – 30ус
Понимание общих принципов выведения тех или иных формул очень помогает при решении нетривиальных упражнений, имеющих схожую задачу, но более высокого уровня.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8270 |
| Номер материала | 456 |