
Урок «Логарифмические неравенства»

Краткое описание документа:
Рассмотрим график логарифмической функции и график прямой пропорциональности
Отметим, что функция возрастает на области определения, Без графика это можно определить по основанию логарифма. Для где х>0, если основание логарифма больше нуля, но меньше единицы, то функция убывает, если основание логарифма больше единицы, то функция возрастает.
Важно заметить, что логарифмическая функция принимает положительные значения на множестве чисел, больших единицы, запишем это утверждение с помощью символов f(x) при x
Прямая пропорциональность y=x в этом случае на промежутке от одного до плюс бесконечности тоже принимает положительные значения, большие одного. Совпадение это или закономерность? Обо всём по порядку.
Неравенства вида называются логарифмическими, где а — положительное число, отличное от 1 и >0,)>0
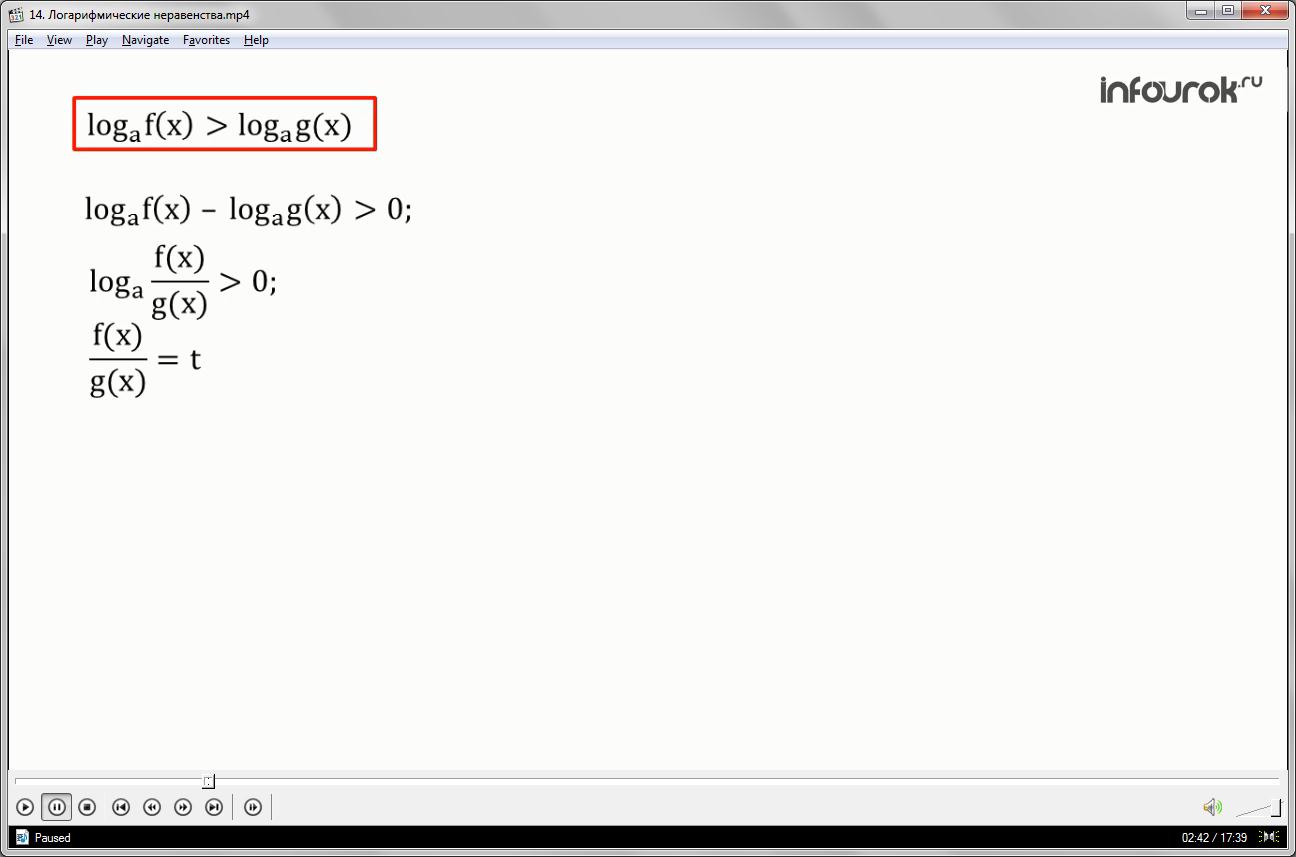
Преобразуем неравенство к виду . При переносе слагаемых из одной части неравенства в другую знак слагаемого меняется на противоположный. По свойству логарифма, разность логарифмов с одинаковым основанием можно заменить логарифм частного, таким образом, наше неравенство примет вид.
Обозначим выражение t, тогда неравенство примет вид.
Рассмотрим это неравенство относительно основания а, большего единицы, и относительно основания а, большего нуля и меньшего единицы.
Если основание логарифма а, большего единицы, то функция возрастает на области определения и принимает положительные значения при t больше одного. Вернемся к обратной замене. Значит, дробь должна быть больше одного. Это означает, что f(x)>g(x).
Если же основание логарифма, большего нуля и меньшего единицы, тофункция убывает на области определения и принимает положительные значения при t больше нуля и меньше одного. При обратной замене неравенство равносильно неравенству , а оно выполняется при f(x)<g(x). При этом важно помнить, что и в первом и во втором случае выражения f(x) и g(x) положительные.
Сделаем вывод:
Если )>0 и при a>1 логарифмическое неравенство
равносильно неравенству того же смысла)>),
а при 0<a<1 логарифмическое неравенство
Равносильно неравенству противоположного смысла )<)
Рассмотрим примеры решения логарифмических неравенств.
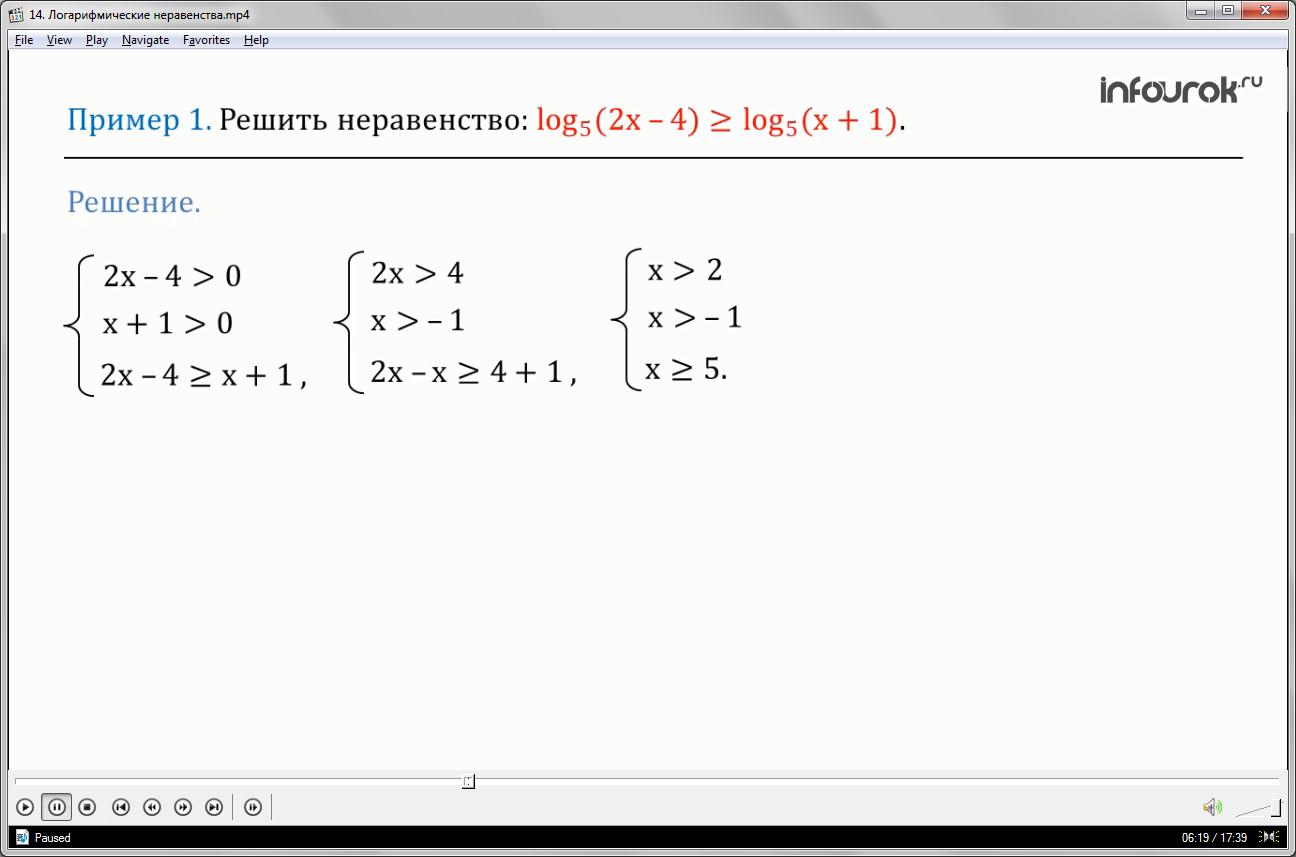
Решить неравенство:
Неравенства >0 и область допустимых значений переменной для данного логарифмического неравенства. Основание логарифма пять и оно больше одного, значит исходное неравенство равносильно неравенству . Решим полученную систему неравенств путем уединения переменной для этого. В первом неравенстве перенесем четыре в правую часть неравенства, поменяв знак минус на плюс. Получим .
Во втором неравенстве единицу перенесем в правую часть и запишем как минус один. Получим неравенство В третьем неравенстве минус четыре перенесем в правую часть, запишем как плюс четыре, а х перенесем в левую часть и запишем как минус икс. Получим неравенство . В нём можно привести подобные слагаемые в левой и правой частях неравенства. Получим неравенство . В первом неравенстве поделим левую и правую часть неравенства на 2. Получим неравенство . Полученная в ходе решения система имеет знак одной направленности, в таких случаях очевидно, что данной системе удовлетворяет множество чисел больше пяти. Легко увидеть, что пять тоже удовлетворяет системе неравенств. В противном случае можно построить геометрическую модель данной системы и посмотреть решение.
Отметим на координатной прямой числа минус один, два и пять. Причем числам –1 и 2 будет соответствовать светлая точка, а числу пять — темная точка. Нанесем «штриховку» справа от 2 для первого неравенства, справа от 1 — для второго неравенства и справа от пяти — для третьего неравенства. Пересечение штриховок указывает на множество чисел, больших и равных пяти. Ответ запишем в виде выражения
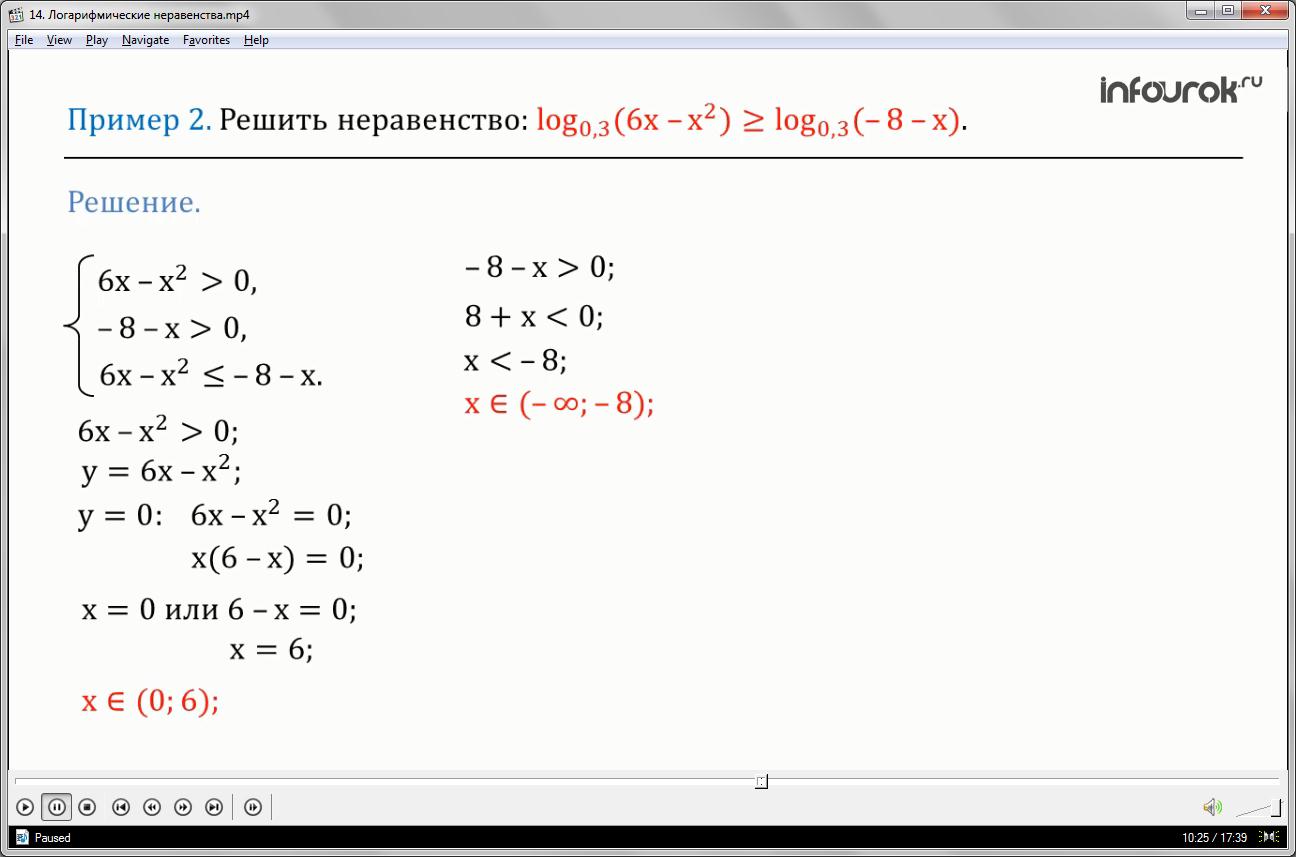
Пример 2. Решить неравенство
Составим систему неравенств. Неравенства >0 и >0 определяют область допустимых значений неравенства. Основание логарифма равно 0,3, оно больше нуля, но меньше одного, значит логарифмическое неравенство равносильно неравенству с противоположным по смыслу знаком:
Полученная система трудна для параллельного решения неравенств. Решим каждое из них отдельно и рассмотрим общее решение на геометрической модели.
Неравенство является квадратным и решается по свойствам квадратичной функции , графиком которой является парабола с ветвями вверх. Найдем нули данной функции, для этого её правую часть приравняем к нулю и решим полученное уравнение через разложение на множители. Для этого вынесем общий множитель икс за скобки, в скобках останется от первого слагаемого — шесть, от второго слагаемого — минус икс. Произведение равно нулю тогда, когда один из множителей равен нулю, а другой при этом не теряет смысла. Значит, первый множитель икс равен нулю или второй множитель шесть минус икс равен нулю. Тогда корни уравнения — ноль и шесть. Отметим их на координатной прямой в виде светлых точек, так как решаемое квадратное неравенство строгое и изобразим параболу ветвями вниз, проходящую через эти точки. Квадратичная функция принимает положительные значения на интервале от нуля до шести, значит решением неравенства является множество чисел x
Неравенство является линейным. Оно содержит отрицательные слагаемые, для удобства обе части неравенства умножим на минус единицу. Знак неравенства в этом случае поменяется на противоположный. Получим неравенство.
Перенесём восемь в правую часть неравенства и запишем как минус восемь. Таким образом, решением неравенства является множество чисел от минус бесконечности до минус восьми. Запишем решение неравенства в иде выражения x.
Неравенство сводится к квадратному неравенству, для этого перенесем минус восемь и минус икс в левую часть неравенства. Получим неравенство и приведем подобные 6х и х, Получим 7х, уравнение примет вид . Решается оно по свойствам квадратичной функции графиком которой является парабола с ветвями вниз. Найдем нули функции.0 при =0 и решим полученное квадратное уравнение через формулу дискриминанта Так как коэффициент b равен минус семи, коэффициент а равен минус единице, а с равен 8 то дискриминант уравнения равен 81. Найдем по формуле первый корень, он равен –1, второй корень равен 8.
Отметим полученные значения на координатной прямой темными точками, так рассматриваемое квадратное неравенство относится к нестрогим неравенствам. Изобразим на координатной прямой параболу с ветвями вниз. Квадратичная функция принимает меньшие и равные нулю значения на множестве чисел от минус бесконечности до включая и от 8 до плюс бесконечности включая 8. Решение этого неравенства запишем в виде выражения ]
Итак, все три неравенства решены, отметим их решения на одной координатной прямой. Значения переменной, которые бы удовлетворяли всем трём неравенствам одновременно, нет, что означает, что исходное логарифмическое неравенство не имеет решений. Ответ: решений нет.
Этот факт можно было заметить после решения линейного неравенства, так как решением первого квадратного неравенства являются положительные числа от одного до шести, а решением второго неравенства являются отрицательные числа, то для этих двух неравенств уже нет общих решений и
исходное логарифмические неравенство не имеет решений.
Логарифмы обладают интересными свойствами, упрощающие вычисления и выражения, вспомним некоторые из них
- Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
- Любое число можно представить в виде логарифма. Например, 2 можно записать как логарифм четырех по основанию два или логарифм 25 по основанию 5, минус единицу можно записать как логарифм 0,2 по основанию пять или десятичный логарифм 0,1.
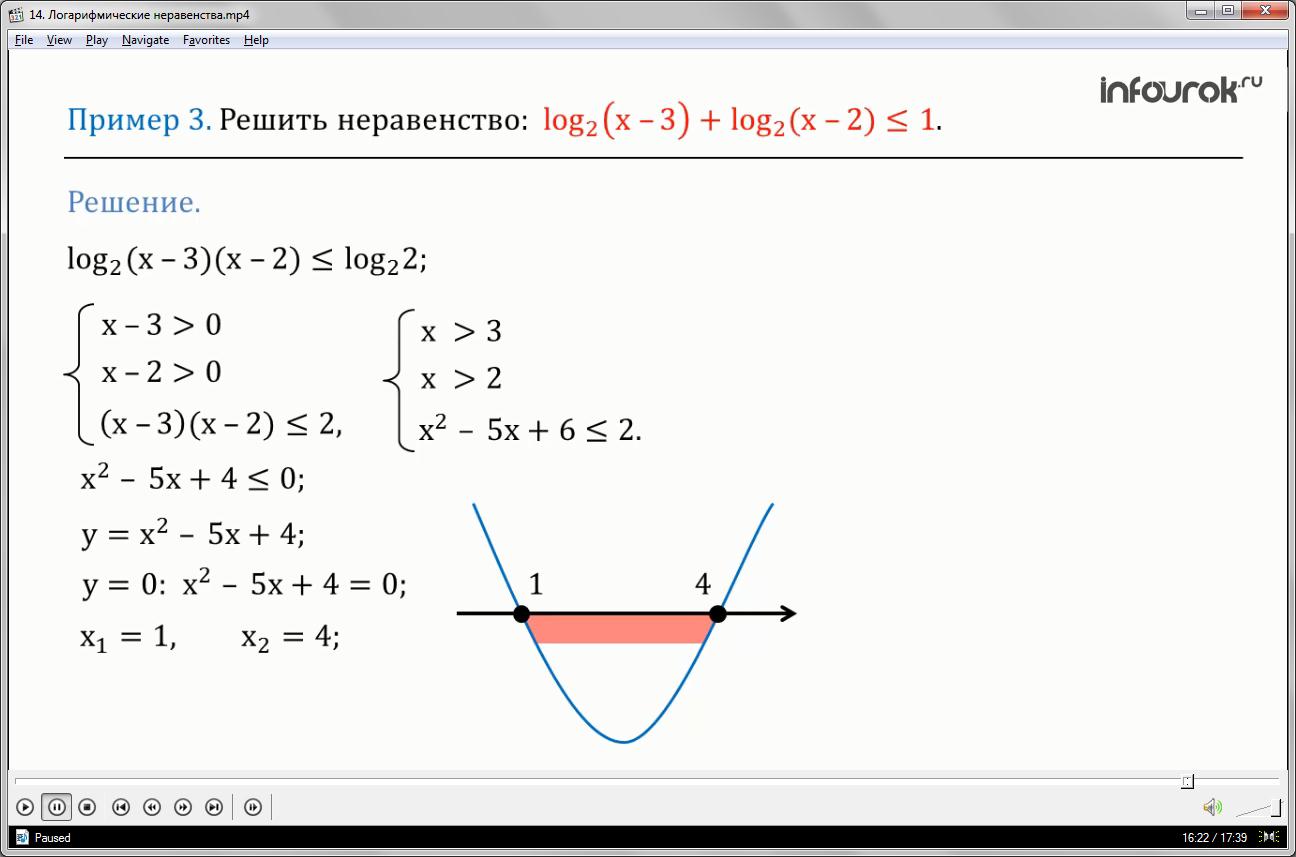
Пример 3. Решить неравенство:
+1.
Неравенство нужно преобразовать к виду.
Для этого единицу запишем в виде логарифма 2 по основанию два. А влевой чатси неравенства сумму логарифмов заменим по свойству на тождественно равное ему выражение — логарифм произведения. Получим неравенство вида
. Составим систему неравенств. Неравенства, задающие область допустимых значений неравенства, опрелеяются по исходному неравенству, поэтому >0 и >0 будут первыми двумя неравенствами системы. Так как логарифм имеет основание 2, оно больше одного, то неравенство
Равносильно неравенству (х-3)(х-2)2.
В первом неравенстве перенесем минус три в правую часть, получим неравенство х>3, во втором — минус два перенесем в правую часть, получим неравенство х>2.
В третьем — раскроем скобки в левой части неравенства, умножая каждый член первого многочлена на каждый член второго многочлена. Получим неравенство .
Решим третье неравенство отдельно: перенесем два в левую часть неравенства и запишем с минусом.
Упростим полученное нравенство до вида . Сумма коэффициентов этого уравнения равна нулю, тогда, по свойству коэффициентов, первый корень равен одному, а второй равен частному от с на а и равен в данном случае 4. Эти уравнения можно решить и через формулу дискриминанта, корни от способа решения не зависят.
Отметим эти корни на координатной прямой в виде тёмных точек, проведем через них параболу ветвями вверх. Неравенство
выполняется на множестве чисел от 1 до 4 включая 1 и 4.
Отметим на одной координатной прямой решение первого и второго неравенства, для этого сделаем штриховку правее трех для первого неравенства и правее двух для второго неравенства и штриховку от 1 до 4 для второго неравенства. Три неравенства одновременно выполняются только на множестве чисел от 3 до 4, включая 4. Значит, это и будет решение исходного логарифмического неравенства.
Вывод: При решении логарифмических неравенств
Если a>1 , то переходят к решению системы из неравенств, определяющих область допустимых значений неравенства, и неравенства подлогорифмических выражений того же знака.
Если 0<a<1 , то переходят к решению системы из неравенств, определяющих область допустимых значений неравенства, и неравенства подлогорифмических выражений противоположного по смыслу знака.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7313 |
| Номер материала | 1063 |