
Урок «Логарифмические уравнения»

Краткое описание документа:
Рассмотрим координатную плоскость. На плоскости изображены графики логарифмических функций у= и у=
Данная геометрическая иллюстрация может являться решением уравнения. По графику мы видим, что уравнение имеет один корень, но точное значение определить сложно. Можно сказать только, что корень лежит на промежутке от 1 до 2.
Заметим, что переменная в данном уравнении находится в подлогарифмическом выражении.
Рассмотрим ещё одну геометрическую модель уравнения. На координатной плоскости изображены две логарифмических функции и g(x)=. По графику легко определить, что x равное 2 является корнем уравнения
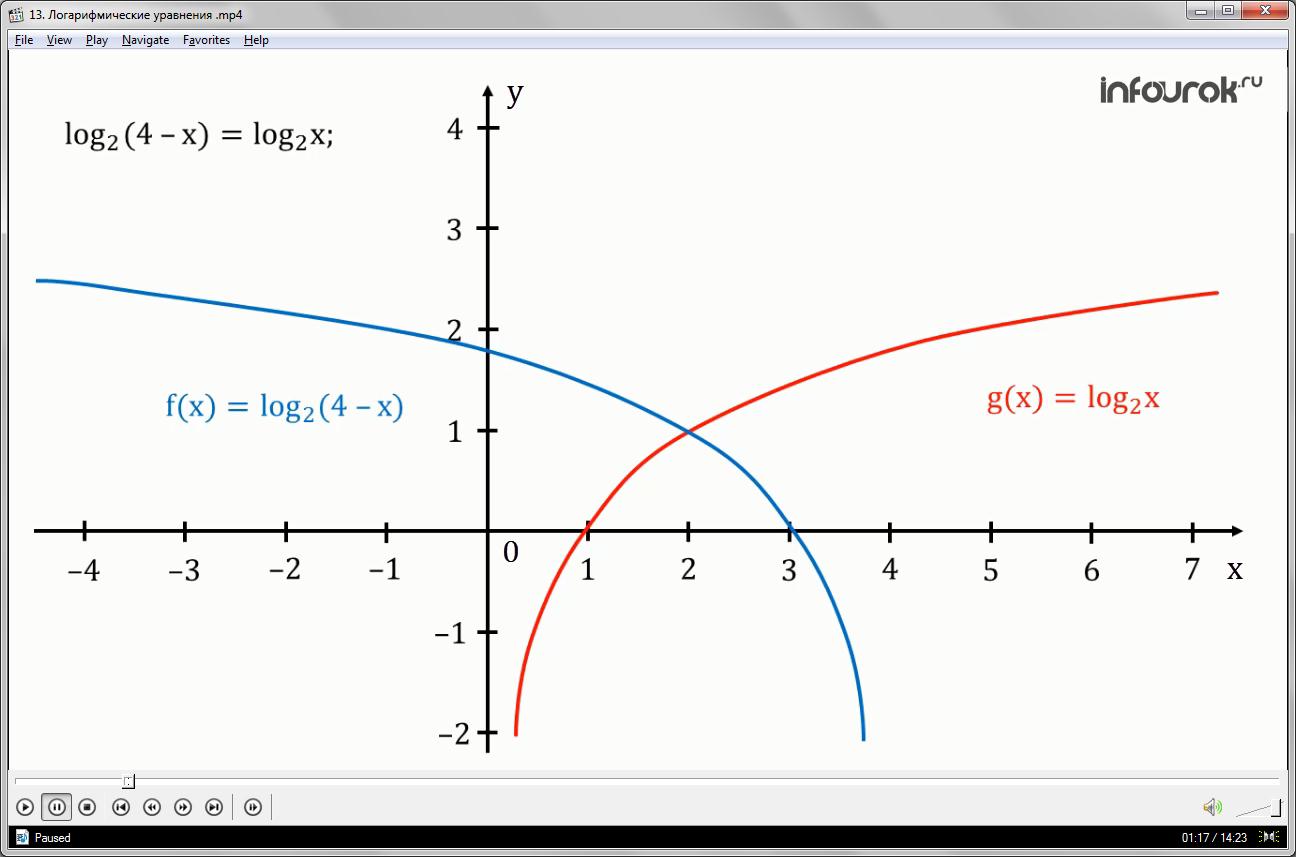
Следует отметить, что х равное 2 входит в область определения функции
и g(x)=.
Рассмотренные уравнения формулируют ряд утверждений и вопросов.
Утверждение первое. Переменная в данных уравнениях находится в подлогарифмических выражениях. Вопрос: К какому типу относятся данные уравнения?
Утверждение второе. Уравнение можно решить графическим способом, но иногда трудно определить значение корня. Возникает вопрос: Как решить уравнение, не используя графическую модель?
Утверждение три. Корень уравнения должен входить в область определения рассматриваемой логарифмической функции. Вопрос: Как учесть область определения функции при решении уравнений не графическим способом?
Попытаемся ответить на возникшие вопросы.
Уравнения вида логарифм f от x по основанию а равен логарифму g от x по основанию а и уравнения сводящиеся к этому виду, где а — положительное число, не равное одному, называются логарифмическими.
корень уравнения, который должен удовлетворять условию f()>о и g()>0.
Рассмотрим уравнение
и его геометрическую иллюстрацию.
В силу монотонности логарифмической функции логарифмы равны на области определения, если равны их подлогарифмические выражения. Таким образом, уравнение
равносильно уравнению 4–х=х при
переход от равенства логарифмов к равенству подлогарифмических выражений при решении уравнений называют потенцированием.
Воспользуемся сделанными выводами и решим данное уравнение способом потенцирования.
Составим условие для выполнения перехода.
Обозначим это условие как ОДЗ – область допустимых значений.
Из левой части уравнения составим неравенство , а из правой . Так как эти неравенства должны выполняться одновременно, объединим их знаком системы. У нас получилась система из двух неравенств с одной переменной. Решением данной системы является промежуток по оси х, которому будет принадлежать корень уравнения. Решим эту систему.
Для этого в первом неравенстве перенесем четыре в правую часть неравенства, изменяя знак четвёрки. Получим. Второе неравенство перепишем. В первом неравенстве поделим обе части неравенства на минус единицу. Получим неравенство Нужно помнить, что при делении или умножении неравенства на отрицательное число знак неравенства меняется на противоположный. Второе неравенство перепишем.
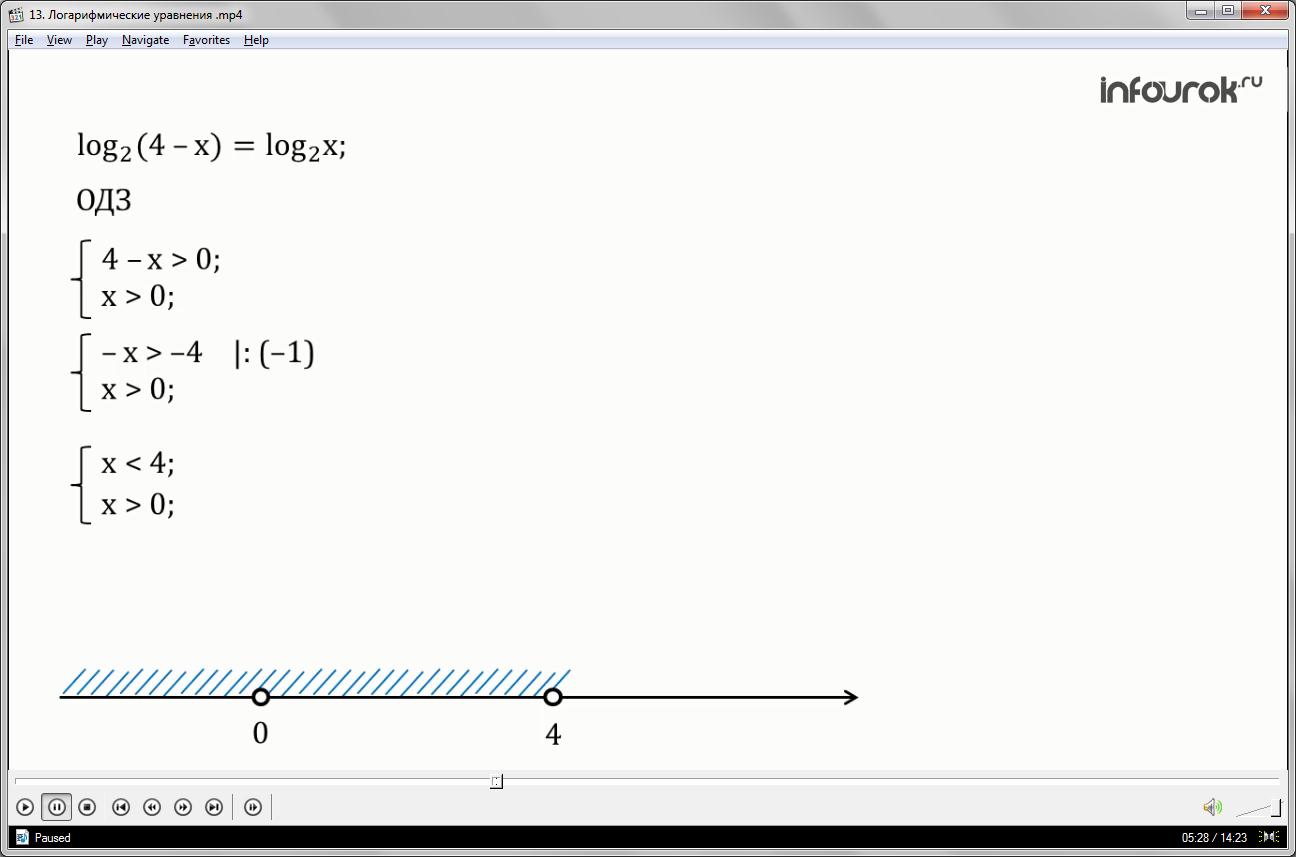
Отметим на одной координатной прямой промежутки, соответствующие полученным неравенствам. Неравенству соответствуют числа левее четырех, отметим их синей штриховкой. Нужно отметить, что данные неравенства являются строгими, и числа ноль и четыре отметим на координатной прямой.
Неравенству соответствуют числа правее нуля. Отметим их красной штриховкой.
Хорошо видно, что неравенства будут выполняться одновременно только для чисел, лежащих между числами ноль и четыре. Запишем их множество в виде выражения.
Для этих чисел исходное уравнение равносильно линейному уравнению.
Решим его путём уединения переменной x.
В уравнении можно переносить слагаемые из одной части уравнения в другую меняя при этом знак слагаемого, поэтому перенесём переменную х из левой части уравнения в правую часть, поменяв знак, получим равносильное уравнение 4=x+x. Приведем подобные слагаемые в правой части уравнения, получим уравнение 4=2х.
Обе части уравнения можно разделить или умножить на любое число не равное нулю, поэтому наше уравнение можно поделить на два, чтобы получить значение переменной х. Четыре поделить на два — получим два, два икс поделить на два — получим икс. Таким образом, икс равен двум.
Проверим полученный корень по условию, определяющему ОДЗ. Число два лежит между числами ноль и четыре, значит, оно лежит в области допустимых значений и является корнем уравнения. Чаще проверка корня, если соответствие условию очевидно, выполняется устно.
Таким образом, по свойствам логарифмической функции решено уравнение без построения графика путем потенцирования. В алгебре этот способ считается одним из основных.
Представляем вашему вниманию таблицу, сопоставляющую два решения: графический и алгебраический.
Сложность графического способа заключается в построении графиков соответствующих функций, поэтому предпочтение отдается алгебраическому способу решения уравнений.
При решении логарифмических уравнений важно уметь правильно решать неравенства и системы неравенств. Вспомним алгоритм решения квадратного неравенства.
Решить неравенство
Квадратные неравенства чаще решаются по свойствам квадратичной функции.
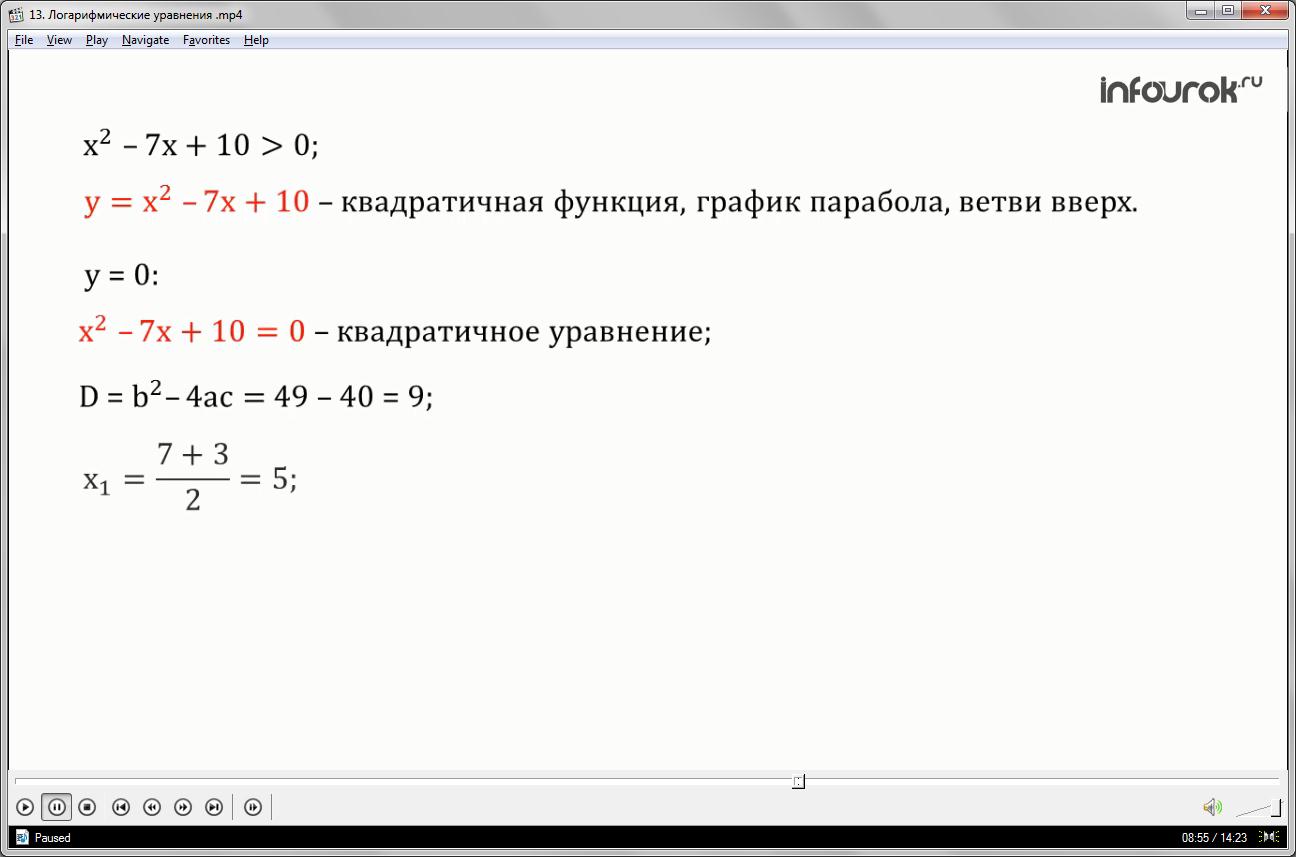
Рассмотрим квадратичную функцию у=, так как коэффициент а равен 1, а это положительное число, то ветви параболы направлены вверх.
Квадратичная функция принимает положительные значения в точках, отличных от нулей функции. Найдём эти точки. Для этого приравняем Данное равенство является квадратным уравнением. Решим его через формулу дискриминанта.
Итак, дискриминант уравнения равен
Подставим значения коэффициентов: b минус семь, а — один, с равен десяти, в результате вычислений дискриминант уравнения равен 9.
Первый корень уравнения равен 5, а второй равен 2.
Отметим эти точки на координатной прямой. В этих точках квадратичная функции принимает нулевые значения, а в остальных точках оси Ох либо положительные, либо отрицательные. Определить это можно по расположению графика функции. Мы выяснили, что парабола расположена ветвями вверх, значит, на промежутке от минус бесконечности до двух и от пяти до плюс бесконечности квадратичная функция принимает положительные значения. Значит, этот промежуток является решением неравенства.
При решении неравенства следует помнить, что все неравенства делятся на строгие и нестрогие.
К строгим относятся неравенства видаf(x)>0, f(0)<0 и им соответствуют обозначения, не включающие значения: круглые скобки и выколотые точки.
К нестрогим неравенствам относятся неравенства вида.
Им соответствуют квадратные скобки и темные точки, включающие значения.
Рассмотрим логарифмическое уравнение.
Графическим методом решить его будет достаточно сложно, поэтому воспользуемся методом потенцирования.
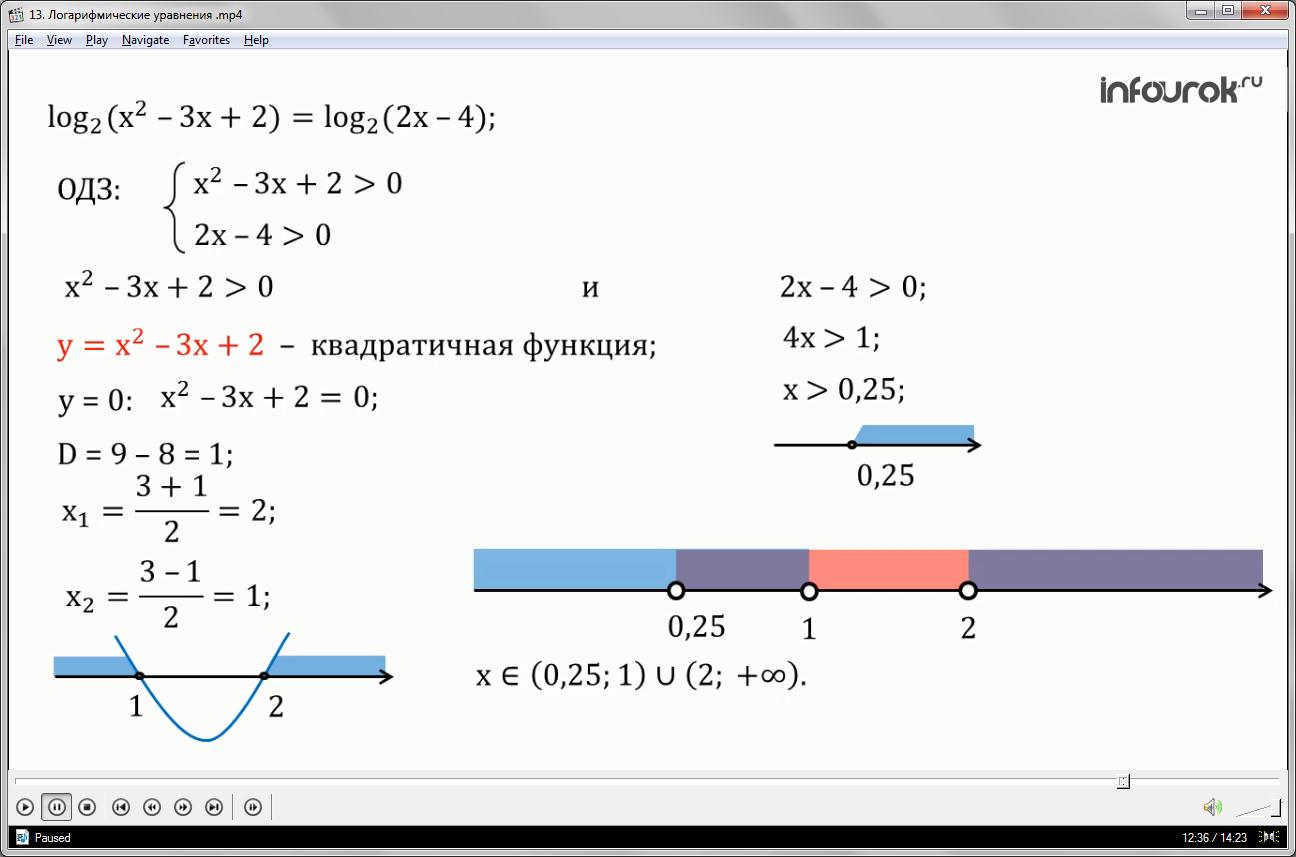
Составим условия, определяющие область допустимых значений (ОДЗ). В уравнении два логарифма, значит в одз будет два условия. Первое .
Решим каждое из неравенств отдельно, а затем найдем общее решение. Первое неравенство.
Повторим алгоритм действий в ранее решенном квадратном неравенстве. Рассмотрим квадратичную функцию у=. Найдем нули этой функции, они равны двум и одному. Отметим их на координатной прямой выколотыми точками один и два, в силу строгости решаемого неравенства.
Промежуток от минус бесконечности до одного и от двух до плюс бесконечности является решением этого неравенства.
Второе условие определяет линейное неравенство . Решим его уединением переменной. Для этого минус один перенесём в правую часть неравенства, поменяв при этом знак минус на плюс, получим . Поделим обе части неравенства на коэффициент четыре, получим линейно неравенство.
Решением этого неравенства является промежуток от 0,25 до плюс бесконечности.
Отметим оба решения на одной координатной прямой. Пересечение промежутков, на изображении их штриховки пересекаются, это множество чисел от 0,25 до одного и от двух до плюс бесконечности. Значит, эти числа образую область допустимых значений и на их множестве возможен переход от равенства логарифмов к равенству подлогарифмических выражений.
То есть исходное уравнение . равносильно уравнению =. Чтобы установить тип нового уравнения, перенесём все слагаемые в левую часть и приведём подобные. Получим уравнение. Это квадратное уравнение и способ его решения очевиден. Дискриминант уравнения равен единице. Первый корень уравнения равен 3 , а второй равен 2.
Проверим найденные корни по условиям, определяющим ОДЗ.Число два не принадлежит найденному множеству чисел, значит не может являться корнем уравнения. Ответ: три.
При решении уравнений, в тех случаях, когда решить систему довольно сложно, можно проверить корни и простой подстановкой корней в условие, определяющее ОДЗ. Мы видим, что корень, равный двум, не удовлетворяет условию, а корень, равный трем, подходит для выполнения и первого и второго условия.
Таким образом, можно сделать вывод, что уравнения, содержащие переменную под знаком логарифма, называются логарифмическими, и основной метод их решения – метод потенцирования. Хотя более сложные уравнения могут решаться комбинацией методов или методом введения новой переменной.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6957 |
| Номер материала | 1062 |