
Урок «Метод координат в пространстве. Прямоугольная система координат»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называются осями координат и обозначаются так: Ох, Оy, Оz, имеют свои названия: ось абсцисс, ось ординат и ось аппликат соответственно, а их общая точка – началом координат. Обычно она обозначается буквой О.
Вся система координат обозначается Охуz.
Если через оси координат Ох и Оу, Оу и Оz, Оz и Ох провести плоскости, то такие плоскости будут называться координатными плоскостями и обозначаться: Оху, Оуz, Оzх соответственно.

Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч — отрицательной полуосью.
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости.
Посмотрим, как это делается.
Проведем через точку М три плоскости, перпендикулярные осям координат, и обозначим через М₁, М₂ и М₃ точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат.
Первая координата точки М (она называется абсциссой и обозначается обычно буквой х) определяется так: х = ОМ₁, если М₁ - точка положительной полуоси;
х= - ОМ₁, если М₁ - точка отрицательной полуоси; х =0, если М₁ совпадает с точкой О.
Аналогично с помощью точки М₂ определяется вторая координата (ордината) у точки М,
а с помощью точки М₃ — третья координата (аппликата) z точки М.
Координаты точки М записываются в скобках после обозначения точки М (х; у; z).
Запомните, что первой указывают абсциссу, второй – ординату, третьей — аппликату.
Задача 1.
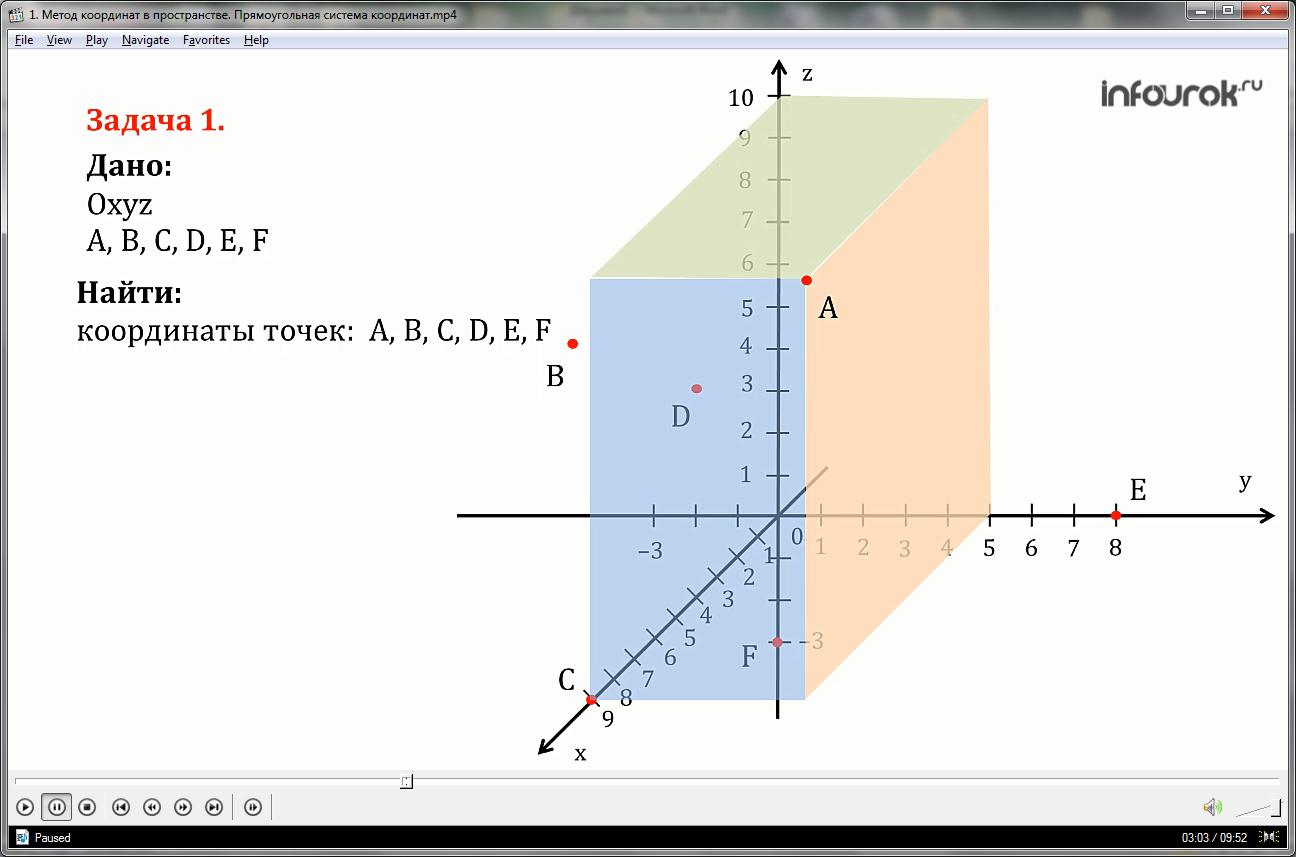
Найдем координаты точек А, В, С, D, E, F, представленные на рисунке.
Проведем через точку А три плоскости, перпендикулярные к осям координат, тогда точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат будут координатами точки А. Точка А имеет координаты: абсцисса = 9, ордината = 5, аппликата = 10 и записывается это так: А (9; 5;10).
Аналогично записываются координаты следующих точек:
Точка В имеет координаты: абсцисса = 4, ордината = -3, аппликата = 6
Точка С имеет координаты: абсцисса = 9, ордината = 0, аппликата = 0
Точка имеет D координаты: абсцисса = 4, ордината = 0, аппликата = 5
Точка Е имеет координаты: абсцисса = 0, ордината = 8, аппликата = 0
Точка F имеет координаты: абсцисса = 0, ордината = 0, аппликата = -3
В (4; -3; 6),
С (9; 0; 0),
D (4; 0; 5),
Е (0; 8; 0),
F (0; 0; -3).
Если точка М (х; у; z) лежит на координатной плоскости на оси координат, то некоторые ее координаты равны нулю.
Если МЄОху (точка М принадлежит плоскости Оху), то аппликата точки М равна нулю: z=0.
Аналогично, если МЄОхz (точка М принадлежит плоскости Оxz), то у = 0, а если МЄОуz (точка М принадлежит плоскости Oyz), то х = 0.
Если МЄОх (точка М лежит на оси абсцисс) ордината и аппликата точки М равны нулю: у=о и z=0. В нашем примере это точка С.
Если МЄОу (точка М лежит на оси ординат), то х=0 и z=0. В нашем примере это точка Е.
Если МЄОz (точка М лежит на оси аппликат), то х = 0 и у = 0. В нашем примере это точка F.
Если все три координаты точки М равны нулю, то это значит, что М=О (0; 0; 0) – начало координат.
Задача 2
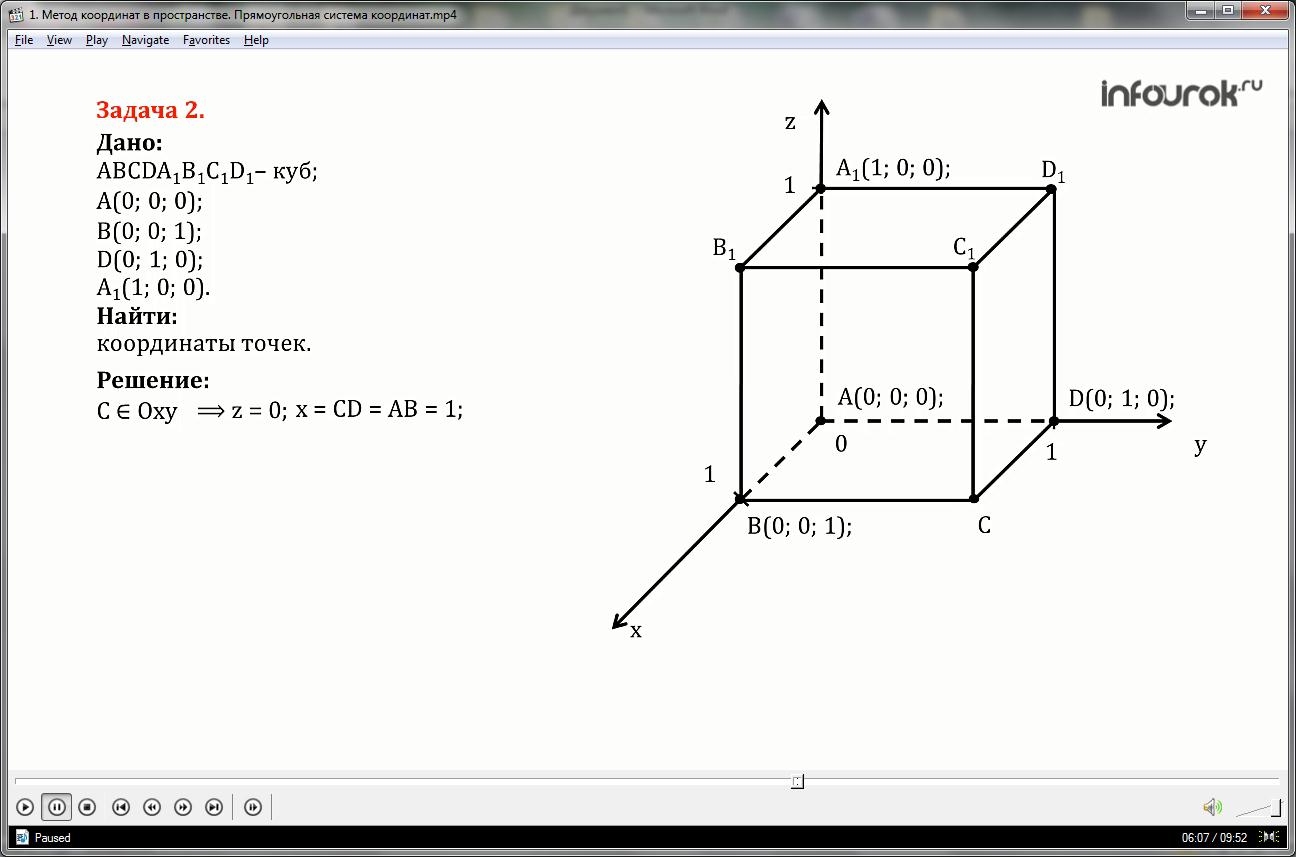
Даны координаты четырех вершин куба ABCDA1B1C1D1: A(0; 0; 0); B(0; 0; 1); D(0; 1; 0); A1(1; 0; 0). Найдите координаты остальных вершин куба.
Решение:
Так как фигура — куб, то все стороны равны единице, все грани являются квадратами.
Точка С принадлежит плоскости Оху, то есть ее координата z равна нулю, координата х равна стороне СД и равна АВ, значит равна единице, координата игрек равна стороне куба СВ, значит равна АД и равна единице.
Аналогично, Точка В1 принадлежи плоскости Охz, то еcть ее координата y равна нулю, координата х равна стороне координата х равна стороне А1B1 и равна АВ значит равна единице, координата зет равна стороне куба В В1значит равна АА1 и равна единице.
Точка Д1 принадлежи плоскости Оуz, то еcть ее координата х равна нулю, координата у равна стороне А1Д1 и равна АД, значит равна единице, координата зет равна стороне куба А1В1 , значит равна АВ и равна единице.
Точка С1 не принадлежит никакой плоскости, то еcть все координаты отличны от нуля, координата х равна стороне C1D1 и равна АB, значит равна единице, координата игрек равна стороне куба В1С1 , значит равна АД и равна единице, и координата зет равна стороне CC1 , то есть AA1 и также равна единице.
Задача 3.
Найдите координаты проекций точки C(; ; ) на координатные плоскости Oxy, Oxz, Oyz и координатные оси Ox, Oy, Oz.
Решение:
1) опустим перпендикуляры на плоскость Oxy— это CN, на плоскость Oxz – CL, и на плоскость Oyz прямая CR.
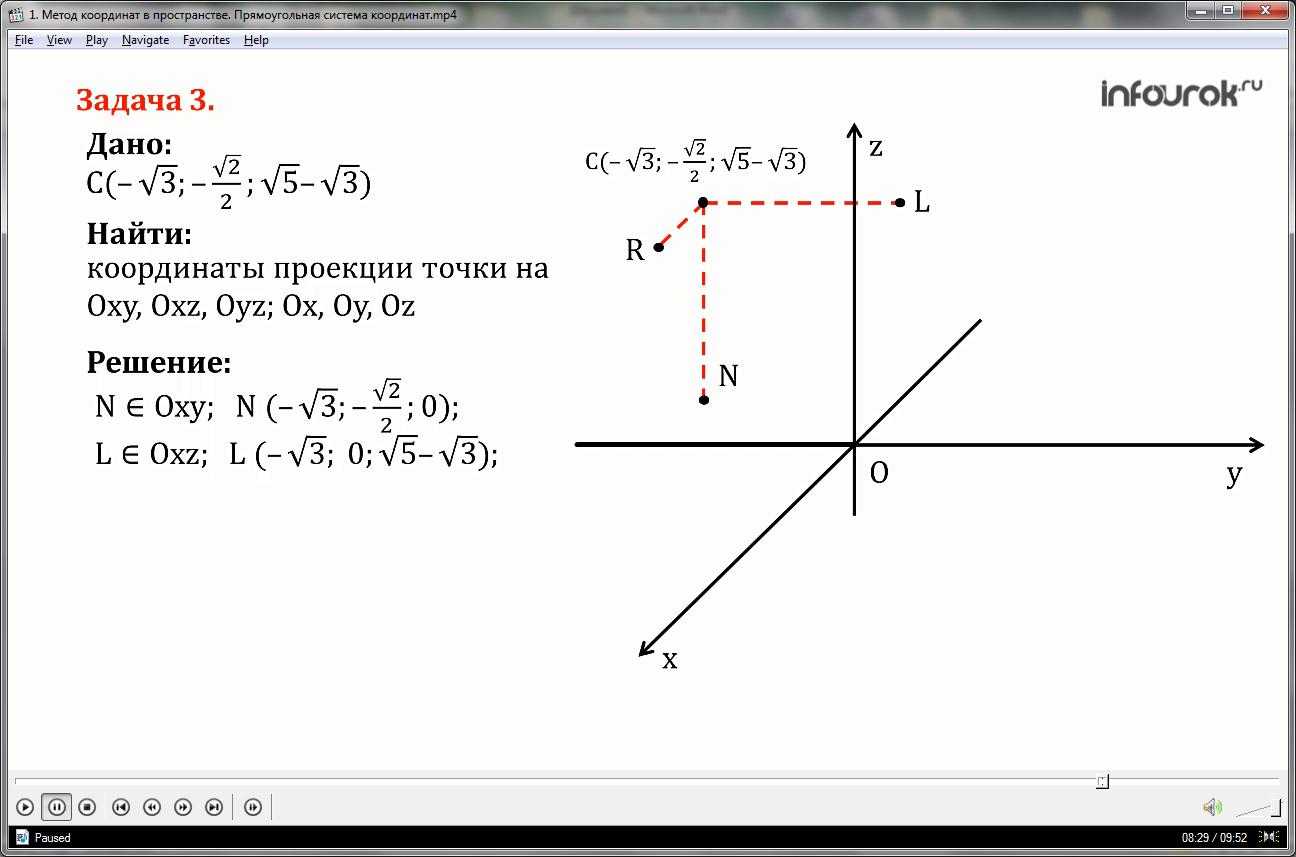
Таким образом, проекция точки С на плоскость Oxy это точка N и она имеет координаты икс равный минус корень из трех, игрек равен минус корень из двух на два, зет равнен нулю.
Проекция точки С на плоскость Oxz – это точка L и она имеет координаты икс равен минус корень из трех, игрек равен нулю, зет равен корень из пяти минус корень из трех.
Проекция точки С на плоскость Oyz– это точка R и она имеет координаты икс равен нулю, игрек равен минус корень из двух на два, зет равен корень из пяти минус корень из трех.
2)Из точки N проводим перпендикуляры на ось Ох – прямая NK, а на Оу – прямая NG, и на ось Оz проводим перпендикуляр из точки R– это прямая RP.
Проекция точки С на ось Ох – точка К имеет координаты икс равный минус корень из трех, а игрек и зет равны нулю.
Проекция точки С на ось Оy– точка G имеет координаты икс и зет равны нулю, игрек равен минус корень из двух на два.
Проекция точки С на ось Оz– точка P имеет координаты икс и игрек равны нулю, зет равный корень из пяти минус корень из трех.
| Автор | |
|---|---|
| Дата добавления | 08.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 15976 |
| Номер материала | 987 |