
Урок «Объемы шарового сегмента, шарового слоя и шарового сектора»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
На уроке мы рассмотрим части шара: шаровой сегмент, шаровой слой и шаровой сектор
Определение. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Секущая плоскость разбивает шар на два шаровых сегмента.
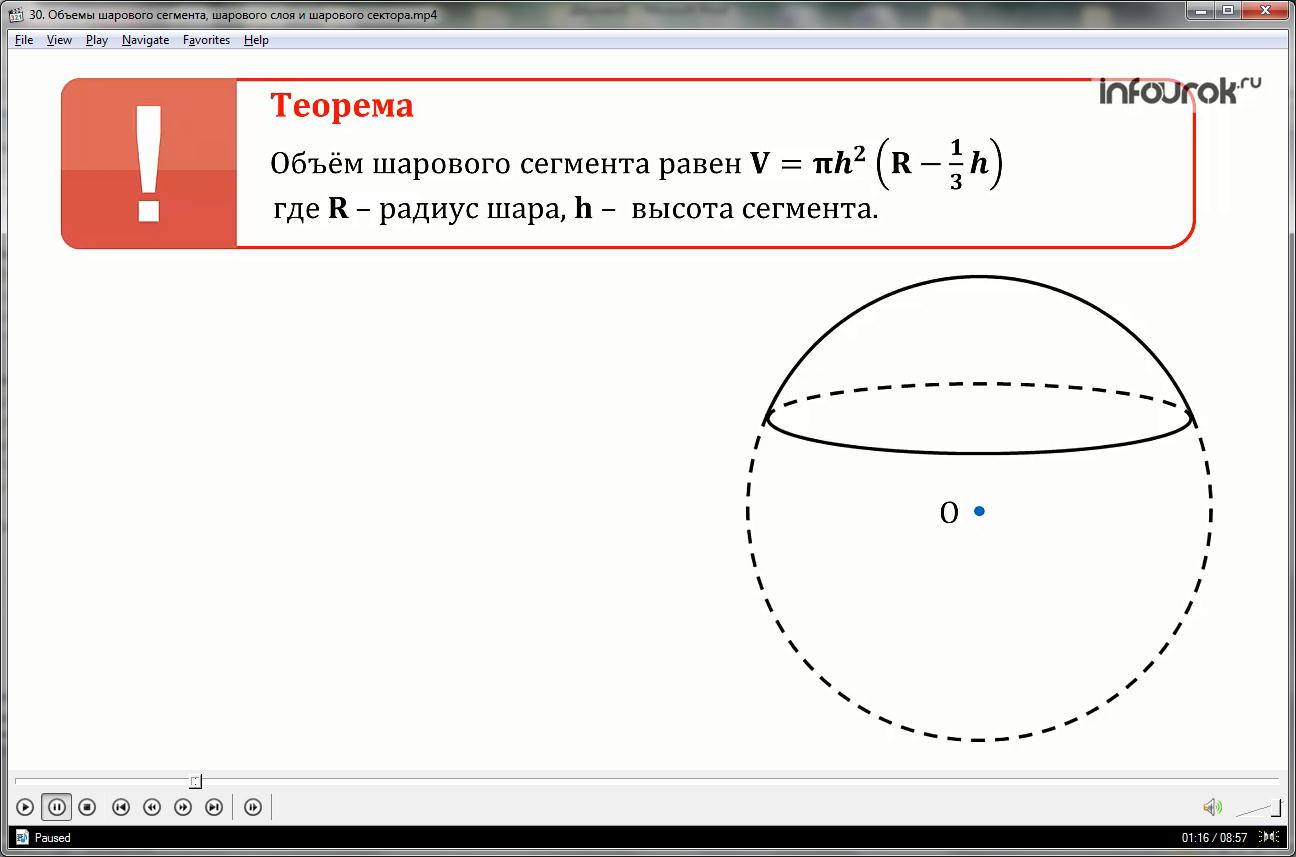
Круг, получающийся в сечении, называется основанием каждого из этих сегментов, а длины отрезков диаметра, перпендикулярного к секущей плоскости, называются высотами сегмента.
На экране высоты сегментов обозначены
Теорема. Объем шарового сегмента равен
где R – радиус шара;
h – высота сегмента.
Доказательство.
Применим уже известную нам интегральную формулу для вычисления объемов тел.
Проведем ось Ox перпендикулярно к плоскости основания.
Тогда произвольное сечение, проведенное перпендикулярно к оси Ox, будет кругом, а его площадь S выражается формулой:
, при R- h<x<R.
Эту формулу мы получили при выводе формулы объема шара.
Вычислив соответствующий определенный интеграл, получаем:
Определение. Шаровым слоем называется часть шара, заключенная между двумя параллельными сечениями.
Расстояние h между сечениями называется высотой слоя, а сами сечения – основаниями слоя.
Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.
Например, объем шарового слоя, изображенного на экране, равен разности объемов шаровых сегментов с высотами AC и BC.
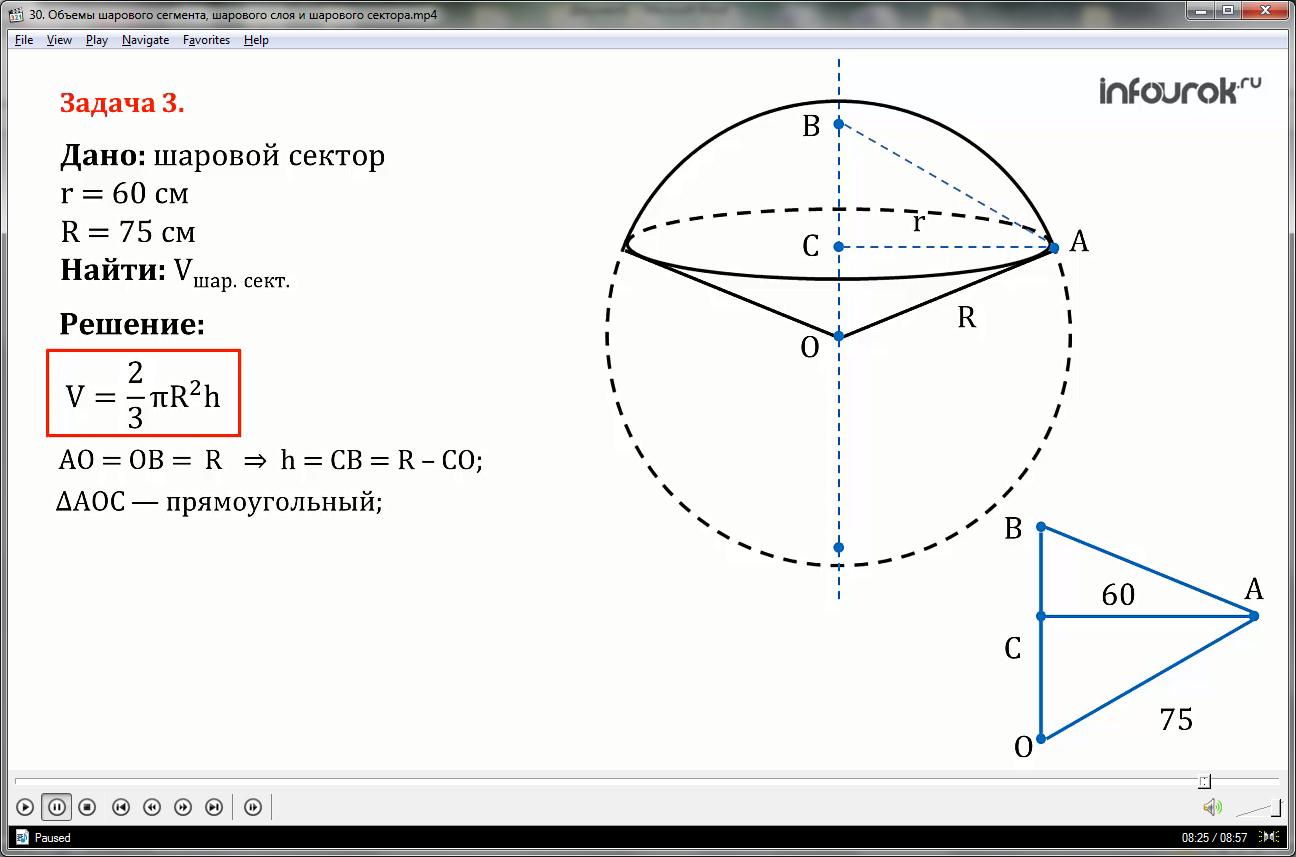
Определение. Шаровым сектором называется тело, полученное вращением кругового сектора с углом меньшим 900, вокруг прямой, содержащей один из ограничивающих сектор радиусов.
Шаровой сектор состоит из шарового сегмента и конуса.
Если радиус шара равен R, а высота шарового сегмента равна h, то объем V шарового сектора вычисляется по формуле:
Переходим к решению задач.
Задача 1
Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объем получившегося шарового слоя, если радиус шара равен R.
Дано:
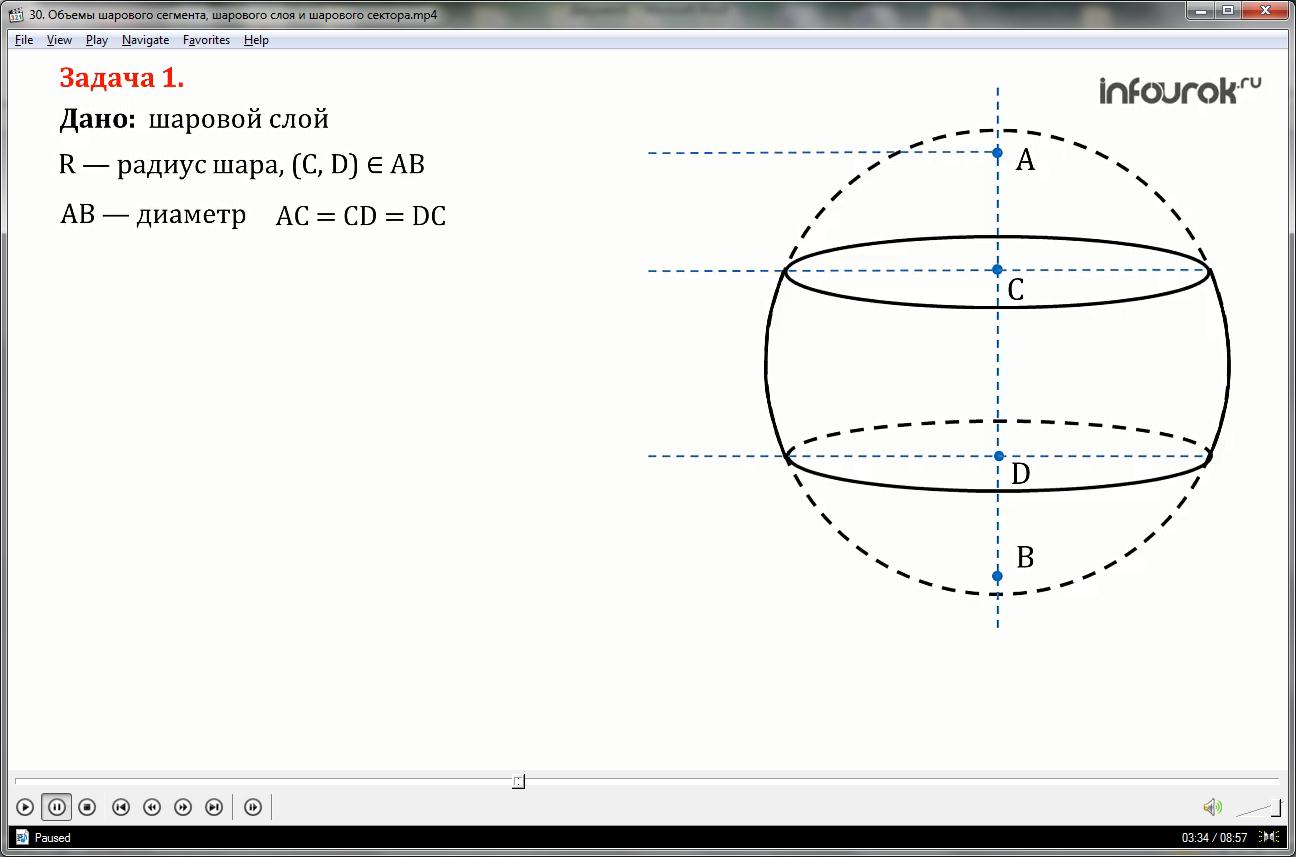
Шаровой слой.
R – радиус шара
D –диаметр, точки C, D делят диаметр на три равные части:
AC = CD = DC
Нужно найти:
Решение:
Объем шарового слоя можно найти как разность объемов двух шаровых сегментов, с высотами AD и AC.
Обозначим высоты сегментов через
На чертеже отрезок AB – диаметр шара и он равен двум радиусам, высота первого сегмента h1 — отрезок AD, высота второго h2 — отрезок AC.
Так как по условию задачи, точки C и D делят диаметр шара AB на три равные части (AC = СD = DB), то
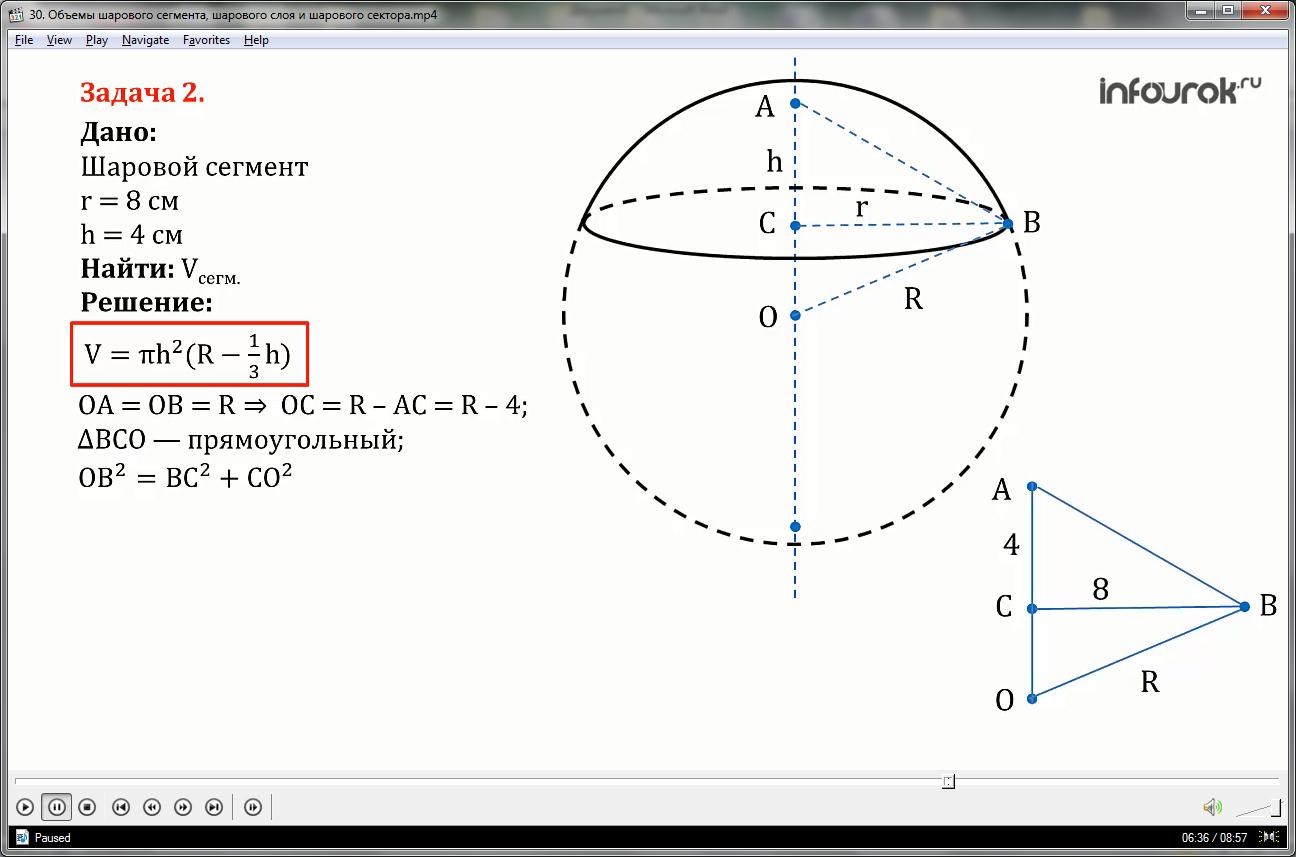
Общая формула для нахождения объема шарового сегмента:
Найдем объем большего сегмента:
Найдем объем меньшего сегмента:
Теперь мы можем вычислить объем шарового слоя, вычислив их разность.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 10768 |
| Номер материала | 1016 |