
Урок «Объем наклонной призмы»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сегодня мы выведем формулу объема наклонной призмы с помощью интеграла.
Вспомним, что такое призма и какая призма называется наклонной?
ПРИЗМА — многогранник, две грани которого (основания) — равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) — параллелограммы.

Если боковые ребра призмы перпендикулярны плоскости основания, то призма прямая, в противном случае призма называется наклонной.
Теорема
Объем наклонной призмы равен произведению площади основания на высоту.
1) Рассмотрим треугольную наклонную призму ВСЕВ2С2Е2. Объем данной призмы равен V, площадь основания — S, высота — h.
Воспользуемся формулой: объем равен интеграл от 0 до h S от икс дэ икс.
V= , где площадь перпендикулярного оси Ох сечения. Выберем ось Ох, причем точка О — начало координат и лежит в плоскости ВСЕ (нижнее основание наклонной призмы). Направление оси Ох перпендикулярно плоскости ВСЕ. Тогда ось Ох пересечет плоскость в точке h, и проведем плоскость Е1 параллельную основаниям наклонной призмы и перпендикулярную оси Ох. Поскольку плоскости параллельны и боковые грани — это параллелограммы, то ВЕ= , СЕ=С1Е1=С2Е2; ВС=В1С1=В2С2

Откуда следует, что треугольники ВСЕ = E2 равны по трем сторонам. Если треугольники равны, значит, равны их площади. Площадь произвольного сечения S(х) равна площади основания Sосн.
S(х)= Sосн.
В данном случае площадь основания является постоянной. В качестве пределов интегрирования возьмем 0 и h. Получаем формулу: объем равен интеграл от 0 до h S от икс дэ икс или интеграл от 0 до h площади основания от икс дэ икс, площадь основания – это константа (постоянная величина), мы можем вынести ее за знак интеграла и получится, что интеграл от 0 до h дэ икс равен аш минус 0:
Получается, что объем наклонной призмы равен произведению площади основания на высоту.
2) Докажем эту формулу для произвольной n- угольной наклонной призмы. Для доказательства возьмем пятиугольную наклонную призму. Выполним разбиения наклонной призмы на несколько треугольных призм, в данном случае — на три (так же, как при доказательстве теоремы об объеме прямой призмы). Обозначим объем наклонной призмы за V. Тогда объем наклонной призмы будет состоять из суммы объемов трех треугольных призм (по свойству объемов).
V=V1+V2+V3, а объем треугольной призмы мы ищем по формуле: объем наклонной призмы равен произведению площади основания на высоту.
VΔ=Sосн∙h
Значит, объем наклонной призмы равен сумме произведений площадей основания на высоту, выносим высоту h за скобки (так как она одинаковая у трех призм) и получаем:
Теорема доказана.
Задача

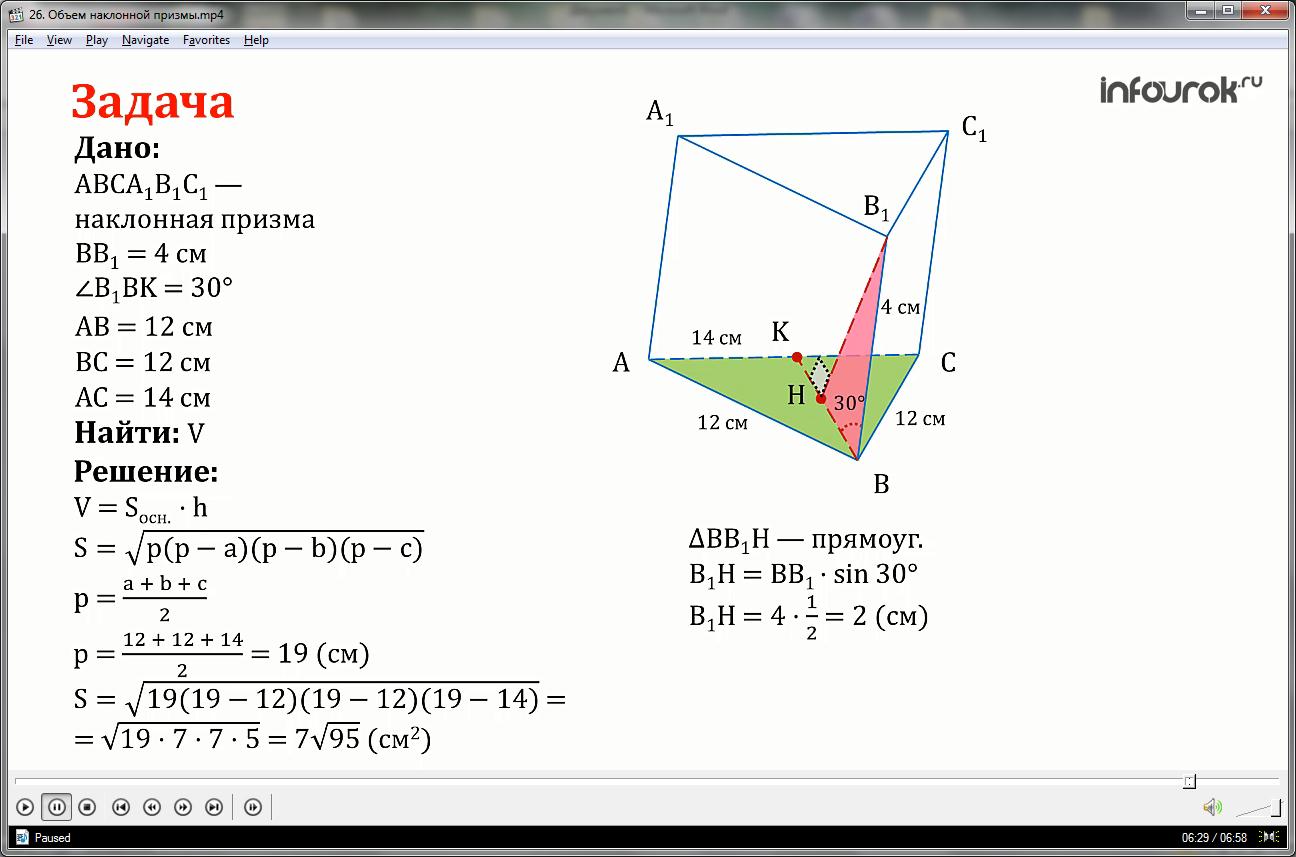
Боковое ребро наклонной призмы — 4 см, составляет с плоскостью основания угол 30°.Стороны треугольника, которые лежат в основании, равны 12, 12, и 14 см. Найти объем наклонной призмы.
Дано: — наклонная призма,
АВ = 12 см, ВС = 12 см, АС = 14 см, В = 4 см, BK = 30° .
Найти: V - ?
Решение.
Дополнительное построение: В наклонной призме проведем высоту Н.
Мы знаем, что объем наклонной призмы равен произведению площади основания на высоту.
В основании наклонной призмы лежит произвольный треугольник, у которого известны все стороны, значит, применим формулу Герона: площадь треугольника равна квадратному корню из произведения пэ на разность пэ и а, на разность пэ и бэ, на разность пэ и цэ, где пэ — полупериметр треугольника, который ищем по формуле: половина суммы всех сторон а, в и с:
считаем полупериметр:
Подставим значение полупериметра в формулу площади основания, упростим и получим ответ: семь корней из 95.
Рассмотрим ΔB H. Он прямоугольный, так как Н – высота наклонной призмы. Из определения синуса, катет равен произведению гипотенузы на синус противолежащего угла
Н = • sin30°
значение синус 30° равен одной второй, значит
Так как
Мы узнали, что
А высота Н – высота наклонной призмы — равна 2.
Следовательно, объем равен
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 25439 |
| Номер материала | 1012 |