
Урок «Объем пирамиды»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Теорема: объем пирамиды равен одной трети произведения площади основания на высоту.
Наша задача вывести формулу для нахождения объема пирамиды. В первом случае возьмем треугольную пирамиду
I. На рисунке треугольная пирамида ОАВС. Пусть V- объем пирамиды ОАВС , S - площадь основания треугольника АВС, ОМ2 - высота пирамиды ОАВС, равная h .
Доказать, что
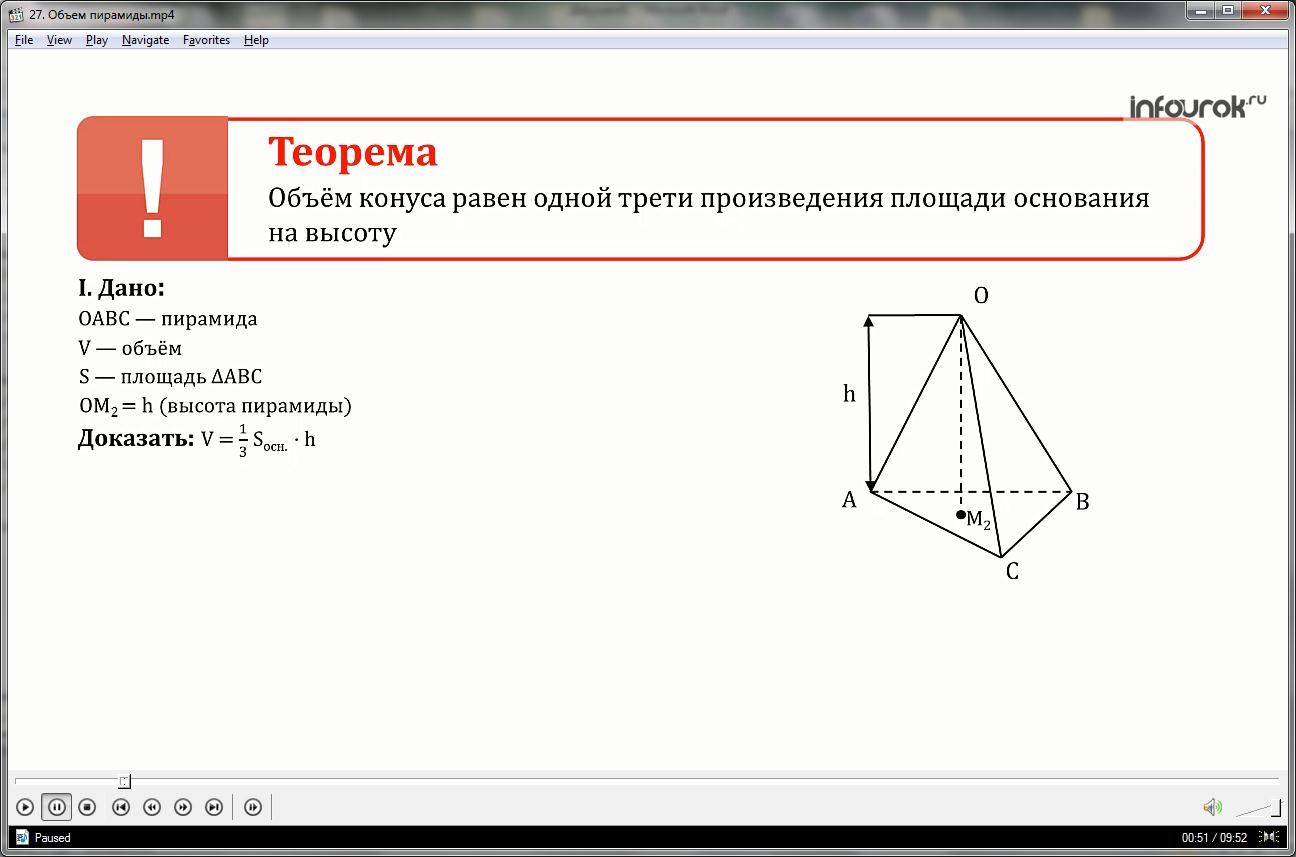
Доказательство:
1) Для доказательства данной теоремы вспомним формулу нахождения объема: объем равен интегралу от 0 до h S от х по dx.
2) Проведем ось координат ох, совпадающую по направлению с высотой, и сечение А1В1С1, параллельное плоскости основания ABC пирамиды.
Длину отрезка ОМ1, где точка М1 — точка пересечения высоты и плоскости А1В1С1, обозначим за х, а через S(x) - площадь сечения. Выразим S(x) через S, h и х.
3) Заметим, что Δ А1В1С1 ΔABC (если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны)
4) Рассмотрим грань параллельна АВ по построению,
тогда , следовательно, из подобия треугольников получаем отношение сторон, т.е. .
5) Сторона А1С1 параллельна АС по построению,
тогда ΔOA1C1 подобен ΔОАС, следовательно, .
А1 С1 так относится к АС, как OC1 к OC.
6) Рассмотрим сторона параллельна ВС,
тогда ΔOВ1C1 ΔОВС, следовательно, из подобия треугольников получаем отношение сторон, то есть .
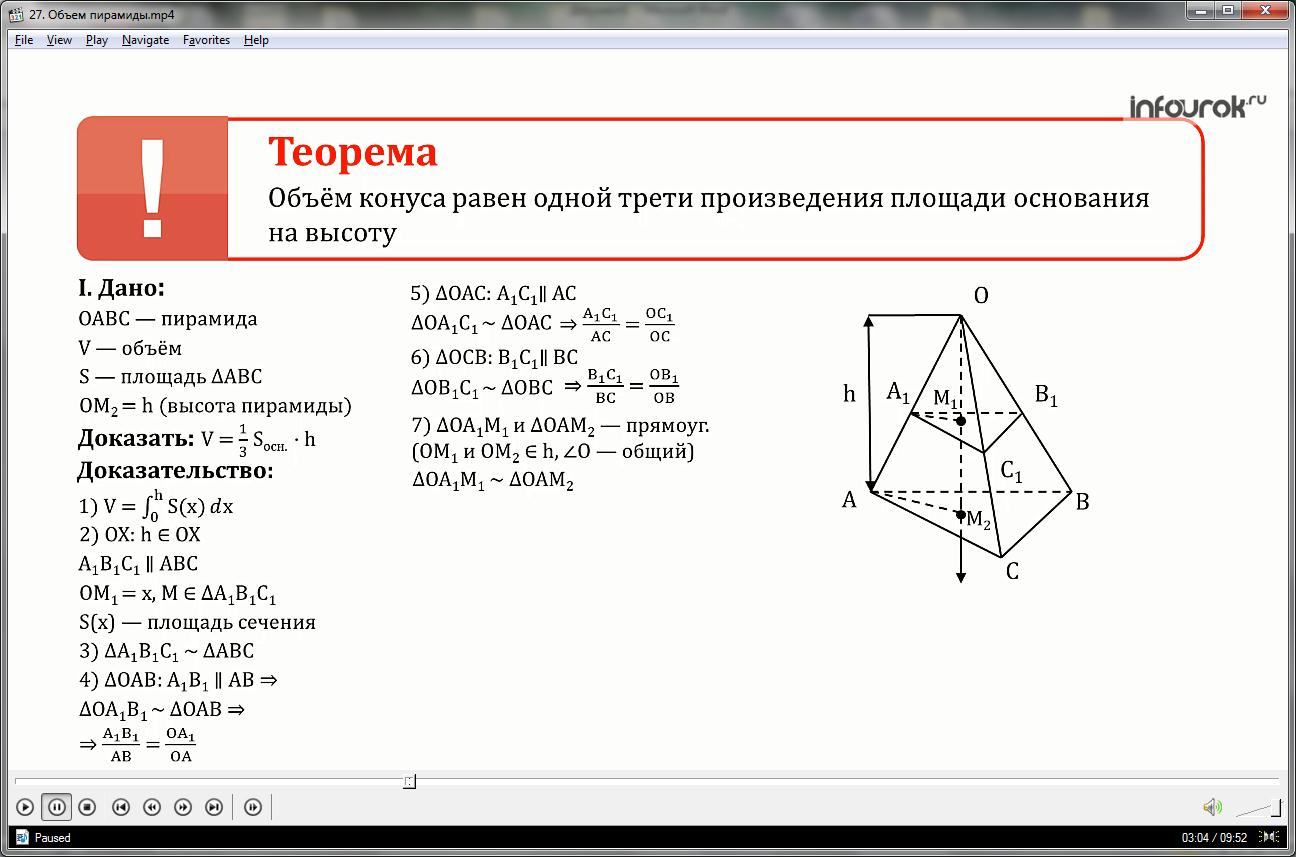
7)Прямоугольные треугольники тоже подобны (они име¬ют прямой угол и общий острый угол при вершине О). В подобных треугольниках стороны одного треугольника пропорциональны соответственным сторонам другого треугольника. Поэтому ОА1 так относится к ОА, как ОМ1 к ОМ2 как х к h.
Так как из ранее доказанного
следовательно, .
Аналогично доказываем , .
Таким образом, ΔА1В1С1 и Δ ABC подобны с коэффициентом подобия . Отношение площадей равно квадрату коэффициента подобия. Следовательно, отношение S от х к S равно квадрату коэффициента подобия:
Выразим из формулы (1) S от х: S от х равно произведению отношения S и квадрата h и квадрата х:
Применим теперь основную формулу для вычисления объемов тел при a = 0, b = h получаем формулу (2):
Объем равен интегралу от 0 до h S от х dx равно интегралу от 0 до h произведения отношения S и квадрата h на квадрат х дэ х, можно вынести отношение S и квадрат h за знак интегрирования, а интеграл от квадрата х равен х в кубе деленный на 3. Подставив пределы интегрирования, мы получим формулу для вычисления объема пирамиды:
II. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S. Такую пирамиду можно разбить на треугольные пи¬рамиды с общей высотой h.
Объем пирамиды OABCDF равен сумме объемов треугольных пирамид
V=VAFDO+VADCO+VABCO
Выразим объем каждой треугольной пирамиды по доказанной нами формуле.
2) Объем пирамиды AFDO равен одной трети произведения площади основания AFD на высоту.
3) Объем пирамиды ADCO равен одной трети произведения площади основания ADC на высоту.
4)Объем пирамиды ABCO равен одной трети произведения площади основания ABC на высоту.
Сложим эти объемы: объем пирамиды равен сумме одной трети произведения площади основания AFD на высоту, одной трети произведения площади основания ADC на высоту, одной трети произведения площади основания ABC на высоту.
Вынося за скобки общий множитель , получим в скобках сумму оснований треугольных пирамид. Объем пирамиды равен одной трети умноженной на высоту и на сумму площадей оснований.
т.е. площадь S оснований исходной пирамиды.
Таким образом, объем исходной пирамиды равен
Теорема доказана.

Решение задач.
Задача 1.
Найдите объем правильной треугольной пирамиды, сторона основания которой равна 1, а высота равна .
Решение:
Объем пирамиды ищем по формуле: объем пирамиды равен одной трети, произведения площади основания на высоту
В основании правильной пирамиды лежит правильный треугольник (равносторонний треугольник).
Найдем площадь треугольника по формуле: Площадь треугольника равна половине произведения сторон на синус угла между ними: S= ∙ a∙b∙ sinα.
В равностороннем треугольнике все углы равны по 60° (сумма углов треугольника равна 180, а углы равны друг другу). Синус 60 градусов равен корень из трех деленный на два.
Стороны равностороннего треугольника равны, значит сторона а равна стороне b:
подставим в формулу площади треугольника: вместо b а, вместо sinα корень из трех на 2 ( ), получим
Итак, площадь основания ищем по формуле: площадь правильного треугольника равна произведению квадрата стороны а и корня из трех, деленного на четыре
Таким образом, в формулу объема пирамиды вместо площади основания подставим формулу (1), получаем объем пирамиды равен одной трети квадрата стороны а и корня из трех, деленного на четыре, умноженной на высоту h:
Подставим в формулу данные значения, получаем: объем пирамиды равен одной трети квадрата единицы и корня из трех, деленного на четыре, умноженной на корень из трех. Умножим корень из трех на корень из трех, получаем корень из девяти или 3, произведем сокращение на 3, получим одну четвертую или 0,25:
Ответ: объём равен 0,25
Задача 2. Дана пирамида, основанием которой является прямоугольник со сторонами 3 и 4. объем пирамиды равен 16. Найдите высоту этой пирамиды.

Решение:
Объем пирамиды ищем по формуле: объем пирамиды равен одной трети, произведения площади основания на высоту
В основании данной пирамиды лежит прямоугольник, значит площадь основания равна произведению длины а на ширину b
Подставим в формулу для вычисления объема пирамиды вместо площади основания формулу (1): объем пирамиды равен одной трети произведения ab и h
Выразим из формулы величину h: высота равна объему пирамиды, разделенному на произведение одной трети а и b
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 23308 |
| Номер материала | 1013 |