
Урок «Вычисление объемов тел с помощью определенного интеграла»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сегодня на уроке мы выведем формулу для вычисления объема тела при помощи определенного интеграла и применения формулы к решению задачи.
Вспомним, что называется определенным интегралом.
Если функция f(x) непрерывна на промежутке I числовой оси, содержащей точки х=а и х=b, то разность значений F(b)-F(a) (где F(x) - первообразная f(x) на I) называется определенным интегралом от функции f(x) от a до b.
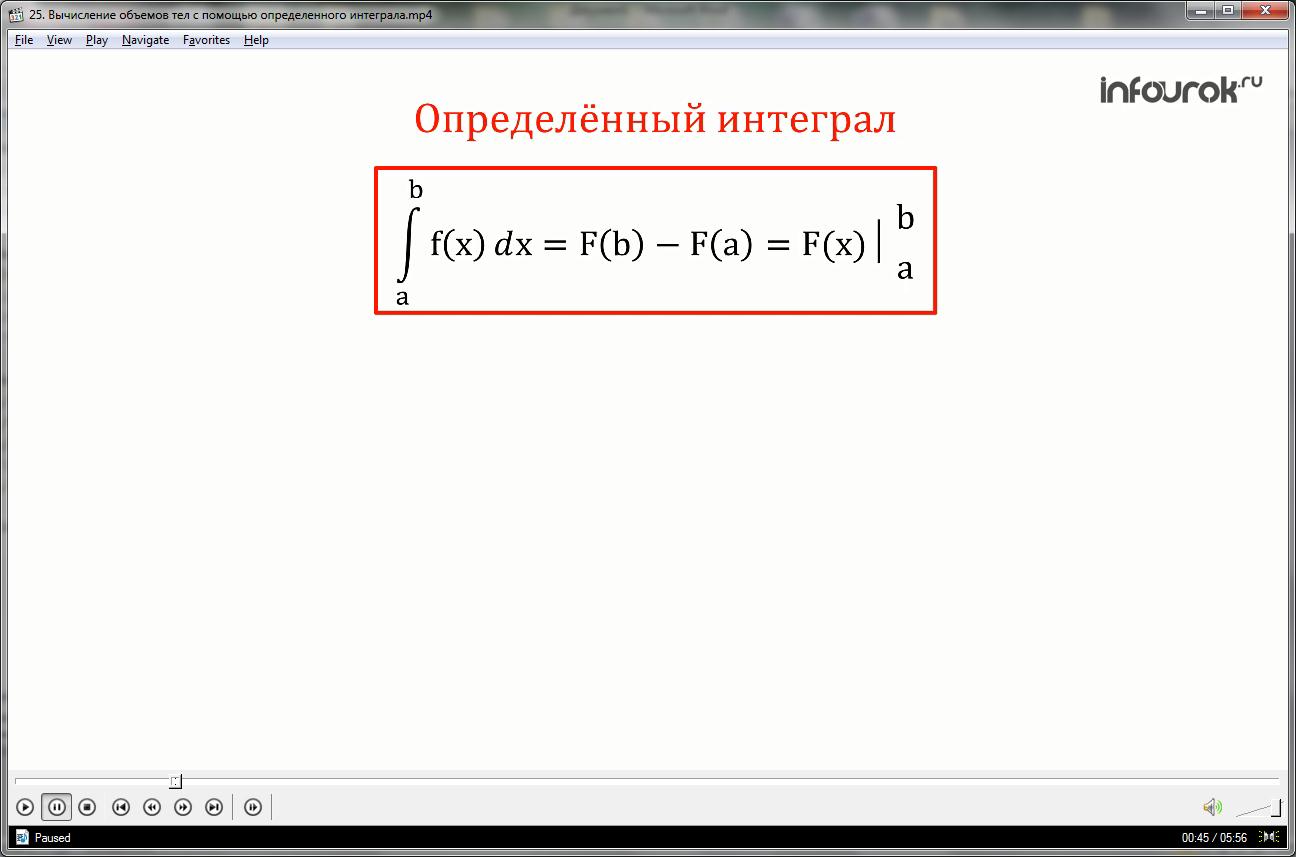
Это формула получила название Ньютона-Лейбница.
(интеграл от a до b эф от икс дэ икс равен разности значений первообразной эф большое от бэ и а)
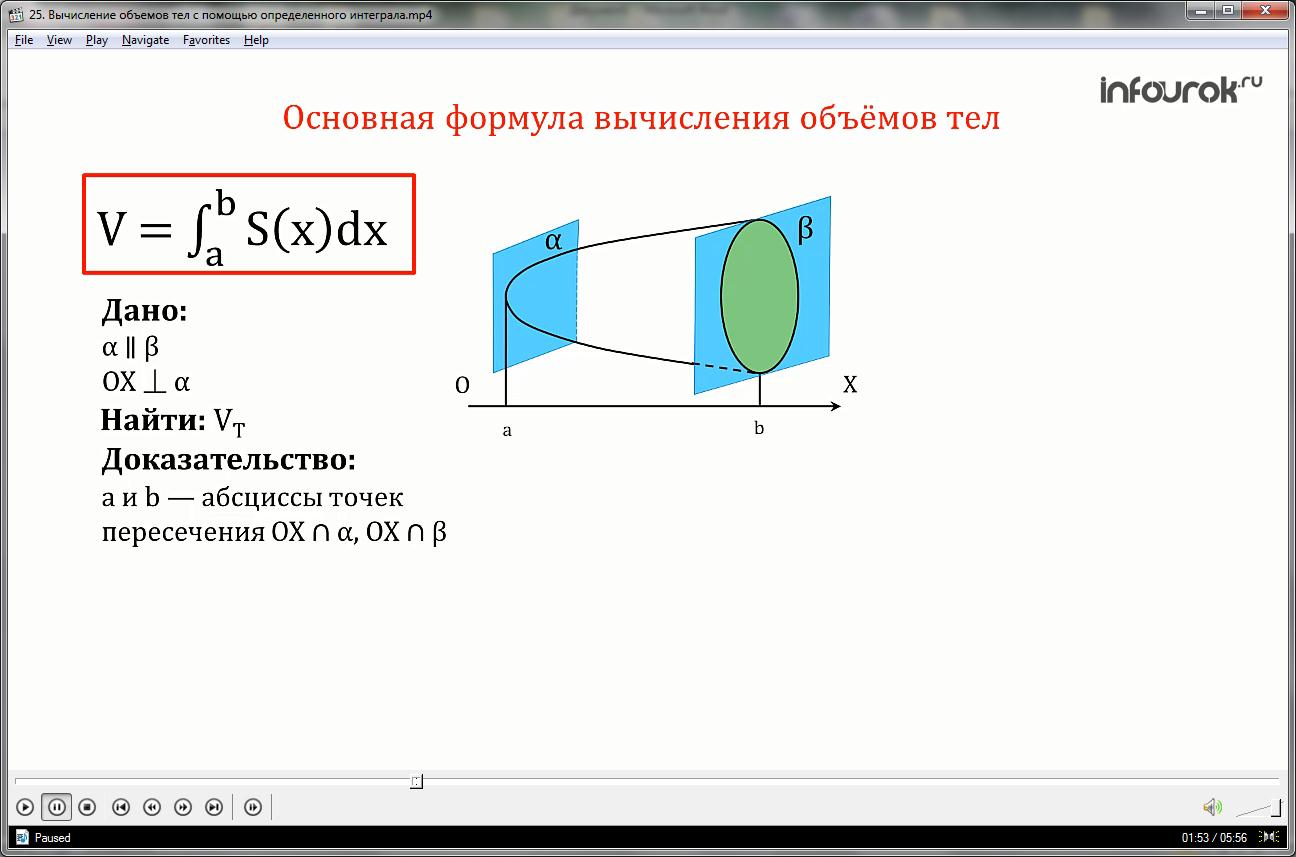
Выведем основную формулу для вычисления объемов тел, основанную на понятии интеграла: объем тела равен интегралу от а до b площади основания фигуры дэ икс,
Доказательство:
Будем рассматривать произвольное тело объёмом V, заключенное между двумя параллельными плоскостями которая перпендикулярна данным плоскостям.
а и b — абсциссы точек пересечения оси ох с этими плоскостями соответственно (а < b).
Рассмотрим сечение данного тела плоскостью, перпендикулярной оси , в данном случае Ф(х), эту фигуру мы будем считать либо кругом, либо многоугольником. Обозначим площадь этой фигуры S(x)=S( ). Далее нам необходимо разделить отрезок [а;b] на n частей. Введем обозначение: а - это , b - это . Расстояние между каждым будет равно
дельта х итое равно отношению разности а и b к n .
Далее рассмотрим тело, которое получается между двумя такими плоскостями. Отрезки разобьют тело на n тел.
Рассмотрим тело, которое получается между двумя такими плоскостями T. Объем этого тела приближенно равен объему призмы, то есть площадь основания фигуры, умноженная на высоту дельта х итое (длину этого отрезка)
S( )
Тогда объем всего тела приближенно равен сумме таких тел Т, то есть сумме по i от одного до n объемов этих тел, то есть сумме эс по х итое на дельта х итое, при этом мы предполагаем, что эс от х итое это непрерывная функция на отрезке [а;b]
Предел данной суммы будет равен объему этого тела, но поскольку это предел интегральной суммы, то он равен интегралу от а до b эс от х дэ х.

Таким образом, мы получили формулу для вычисления объема произвольного тела через площадь перпендикулярного сечения. Объем тела равен интегралу от а до b площади основания фигуры дэ х
Найдем объёмы тел, используя полученную формулу.
Задача.
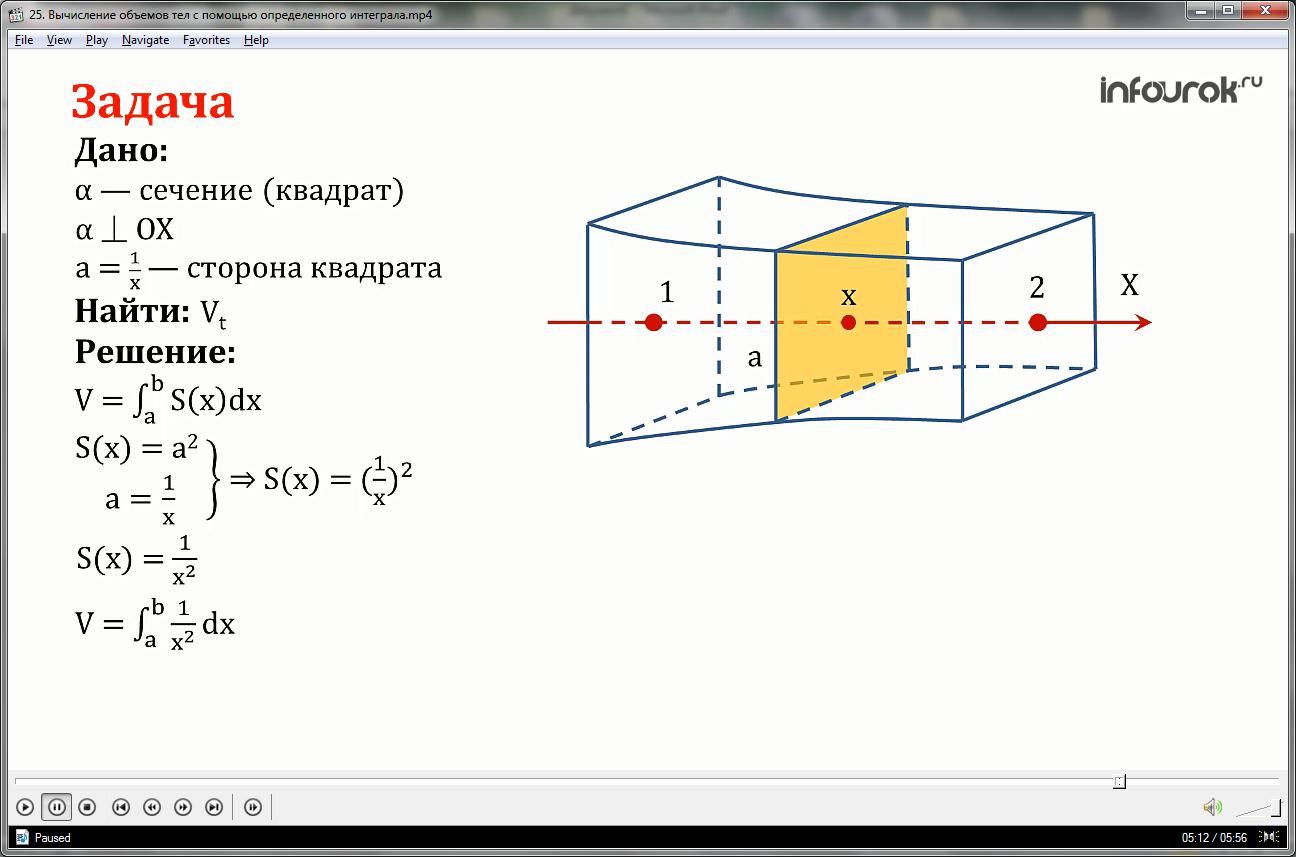
Найти объем тела, изображенного на рисунке, если сечение этого тела плоскостью, перпендикулярной к оси Ох и проходящей через точку с абсциссой х, является квадратом, сторона которого равна .
Дано: сечение — квадрат
Найти
Решение: рассмотрим рисунок
На основании выведенной нами формулы объем тела равен определенному интегралу от а до b эс от х дэ х
Площадь квадрата будем искать по формуле
S(х)= , значит эс от х равна квадрату стороны квадрата, подставим вместо а единицу деленную на х , получим
Подставим данное значение в формулу для нахождения объема при помощи определенного интеграла: объем тела равен определенному интегралу от а до b от b в восьмой степени дэ х
Первообразную степенной функции
Тогда формула (1), примет вид: объем тела равен интегралу от 1 до 2 единицы деленной на х в квадрате дэ х, равен минус единице деленной на х от 1 до 2, подставим значения пределов интегрирования два и один, получим 0,5.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 21892 |
| Номер материала | 1011 |