
Урок «Объем конуса»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем изучение раздела стереометрии «Тела вращения».
К телам вращения относят: цилиндры, конусы, шары.
Вспомним, определения.
Высота – это расстояние от вершины фигуры или тела до основания фигуры (тела). Иначе – отрезок, соединяющий вершину и основание фигуры и перпендикулярный ему.
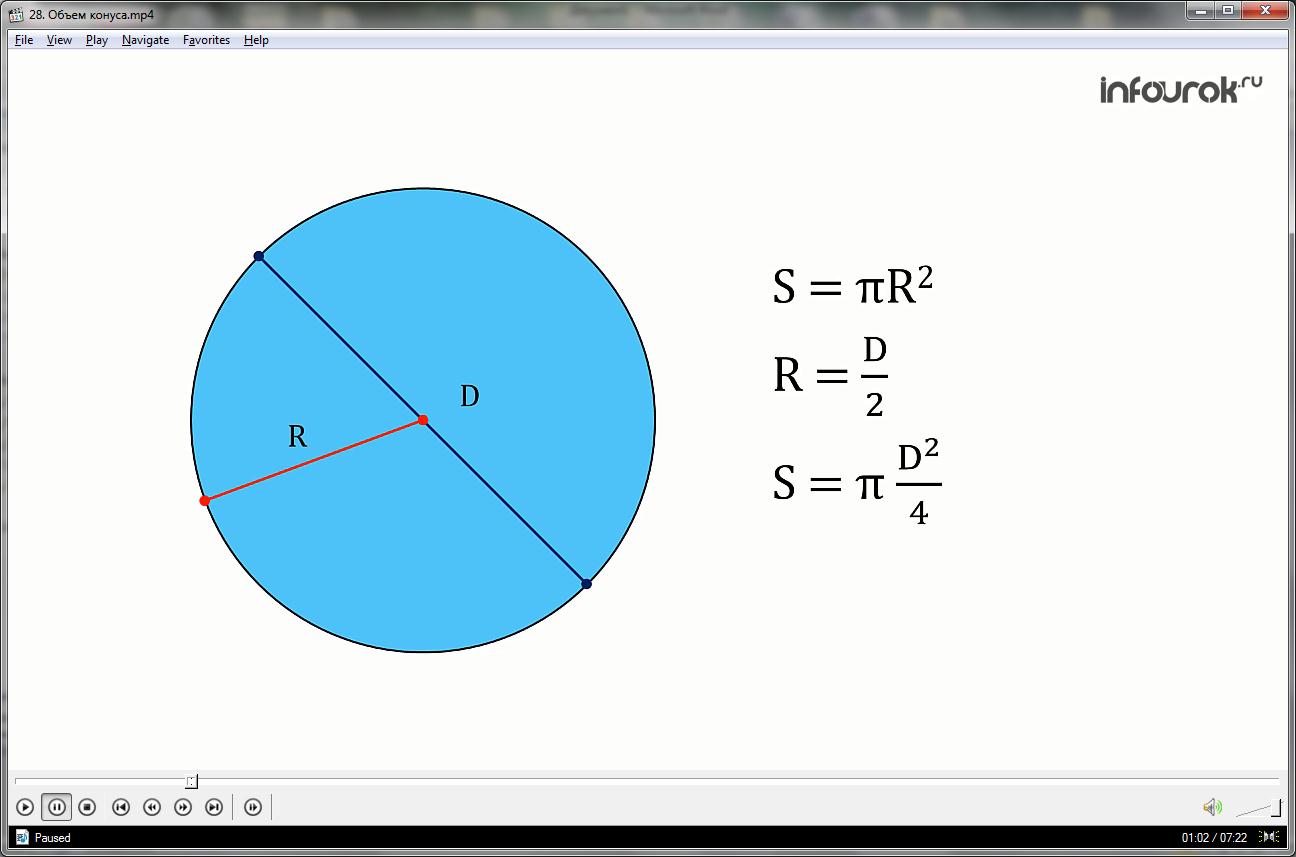
Вспомним, чтобы найти площадь круга нужно пи умножить на квадрат радиуса .
Площадь круга равна .
Вспомним, как найти площадь круга, зная диаметр? Так как
подставим в формулу:
Конус тоже является телом вращения.
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основа¬ния.
Познакомимся с формулой нахождения объема конуса.
Теорема. Объем конуса равен одной трети произведения площади основания на высоту.
Докажем данную теорему.
Дано: конус, S — площадь его основания,
h — высота конуса
Доказать: V=
Доказательство: Рассмотрим конус объемом V, радиусом основания R, высотой h и вершиной в точке O.
Введем ось Оx через ОМ — ось конуса. Произвольное сечение конуса плоскостью , перпендикулярной к оси Ох, является кругом с центром в точке
М1 – точке пересечения этой плоскости с осью Ох. Обозначим радиус этого круга через R1, а площадь сечения через S(х), где х — абсцисса точки М1.
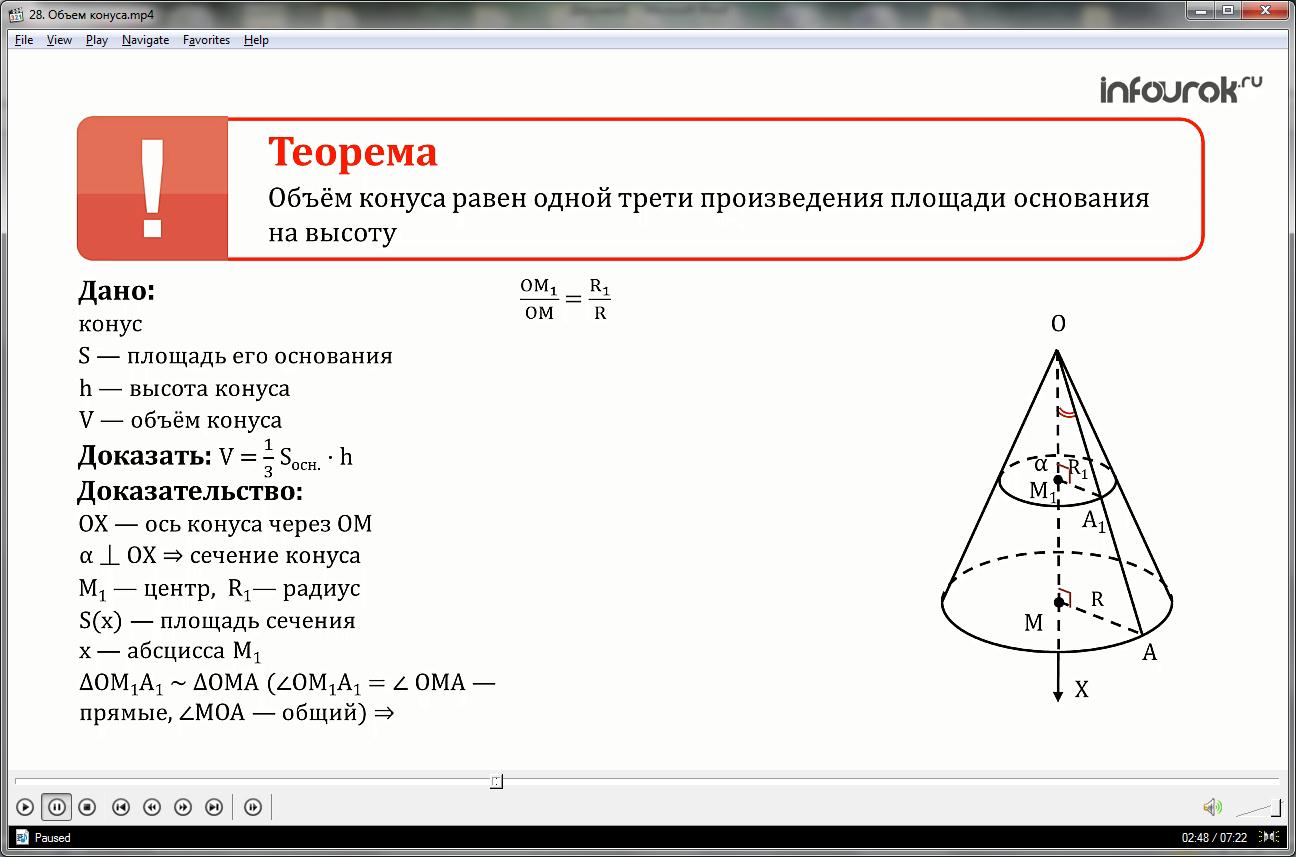
Из подобия прямоугольных треугольников ОМ1A1 и ОМА (ے ОМ1A1 = ے ОМА — прямые, ےМОА-общий, значит, треугольники подобны по двум углам) следует, что
Из рисунка видно что ОМ1=х, OM=h
или откуда по свойству пропорции находим R1 = .
Поскольку сечением является круг, то S(х)=πR12 , подставим вместо R1 предыдущее выражение, площадь сечения равна отношению произведения пи эр квадрата на квадрат х к квадрату высоты:
Применим основную формулу
вычисления объёмов тел, при а=0, b=h, получим выражение (1)
Так как основание конуса – круг, то площадь S основания конуса будет равна пи эр квадрат
в формуле вычисления объема тела заменим значение пи эр квадрат на площадь основания и получим, что объем конуса равен одной трети произведения площади основания на высоту
Теорема доказана.
Следствие из теоремы (формула объема усеченного конуса)
Объем V усеченного конуса, высота которого равна h, а площади оснований S и S1, вычисляется по формуле
Вэ равно одна третья аш умноженное на сумму площадей оснований и корня квадратного из произведения площадей основания.
Решение задач
Задача 1.
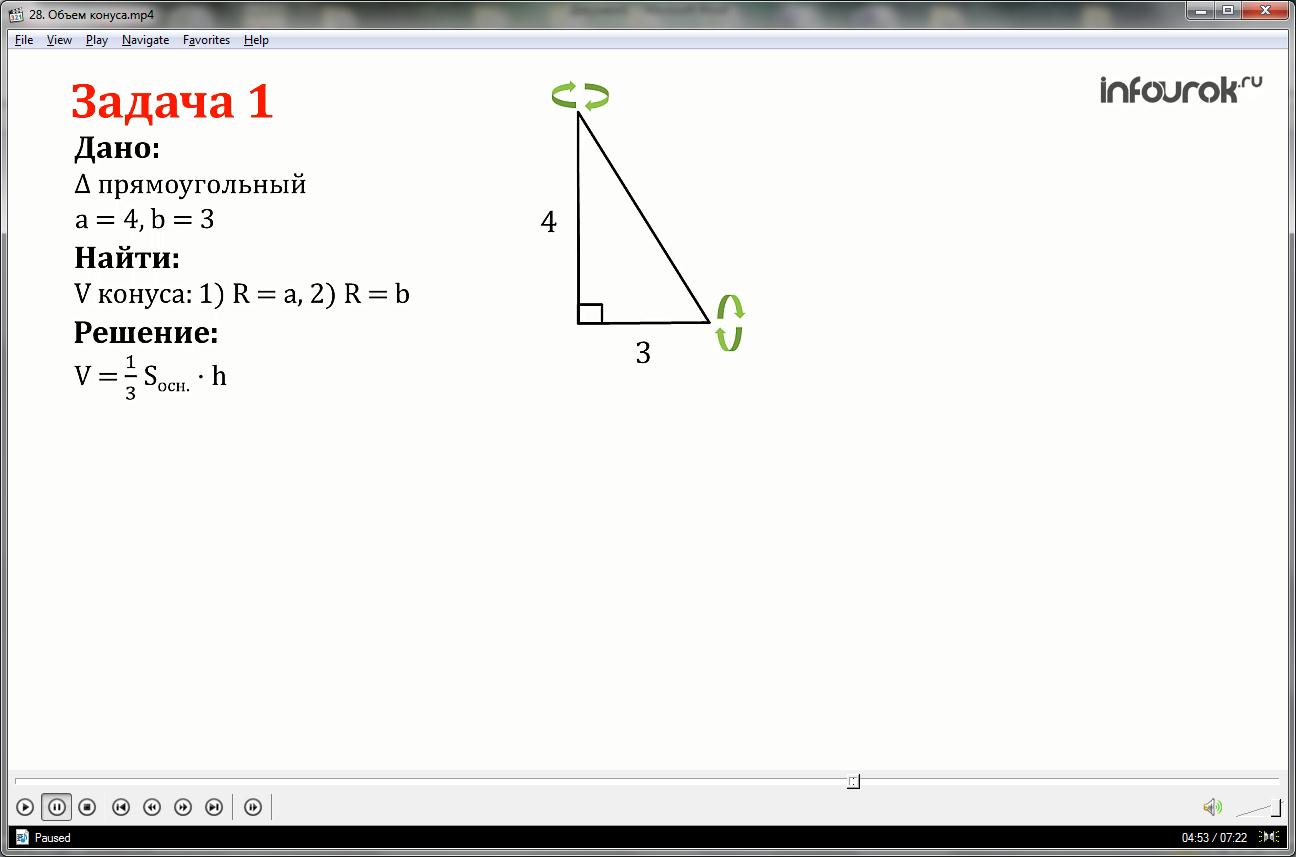
Прямоугольный треугольник с катетами 3 см и 4 см вращается около гипотенузы. Определите объем полученного тела.
Решение:
При вращении треугольника вокруг гипотенузы получаем конус. При решении данной задачи важно понимать, что возможно два случая. В каждом из них мы применяем формулу для нахождения объема конуса: объем конуса равен одной трети произведения основания на высоту
В первом случае рисунок будет выглядеть следующим образом: дан конус. Пусть радиус r = 4, высота h = 3
Объем конуса равен одной трети произведения площади основания на высоту:
Площадь основания равна произведению π на квадрат радиуса
Тогда объем конуса равен одной трети произведения π на квадрат радиуса и на высоту.
V= πR2h
Подставим в формулу значение, получается, объем конуса равен 16π.
Во втором случае вот так: дан конус. Пусть радиус r = 3, высота h = 4
Объем конуса равен одной трети произведения площади основания на высоту:
Площадь основания равна произведению π на квадрат радиуса:
Sосн=πR2
Тогда объем конуса равен одной трети произведения π на квадрат радиуса и на высоту:
V= πR2h
Подставим в формулу значение, получается, объем конуса равен 12π.
Ответ: Объём конуса V равен 16 π или 12 π
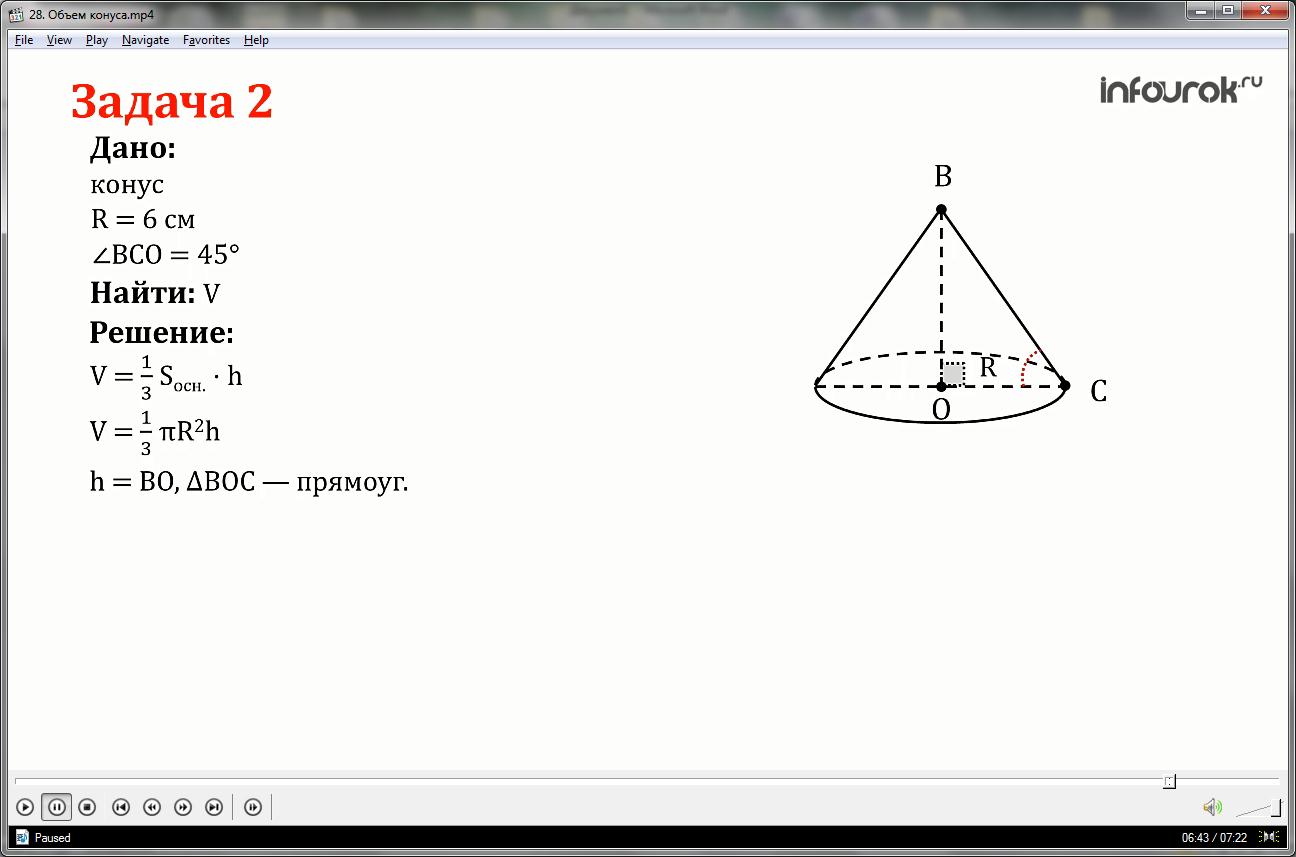
Задача 2. Дан прямой круговой конус с радиусом 6 см, угол ВСО = 45 .
Найдите объем конуса.
Решение: К данной задаче дается готовый чертеж.
Запишем формулу для нахождения объема конуса:
Выразим её через радиус основания R:
Находим h =BO по построению, – прямоугольный, т.к. угол ВОС=90 (сумма углов треугольника), углы при основании равны, значит треугольник ΔBOC равнобедренный и BO=OC=6 см.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 15907 |
| Номер материала | 1014 |