
Урок «Метод математической индукции»

Краткое описание документа:
Видеоурок «Метод математической индукции» помогает освоить метод математической индукции. Видео содержит материал, помогающий понять суть метода, запомнить особенности его применения, научится применять данный метод при решении задач. Цель данного видеопособия – облегчить освоение материала, формировать умения решать математические задачи методом индукции.
Для удержания внимания учащихся на изучении материала используются анимационные эффекты, иллюстрации, представление информации в цвете. Видеоурок освобождает время учителя на уроке для улучшения качества индивидуальной работы, решения других учебных задач.
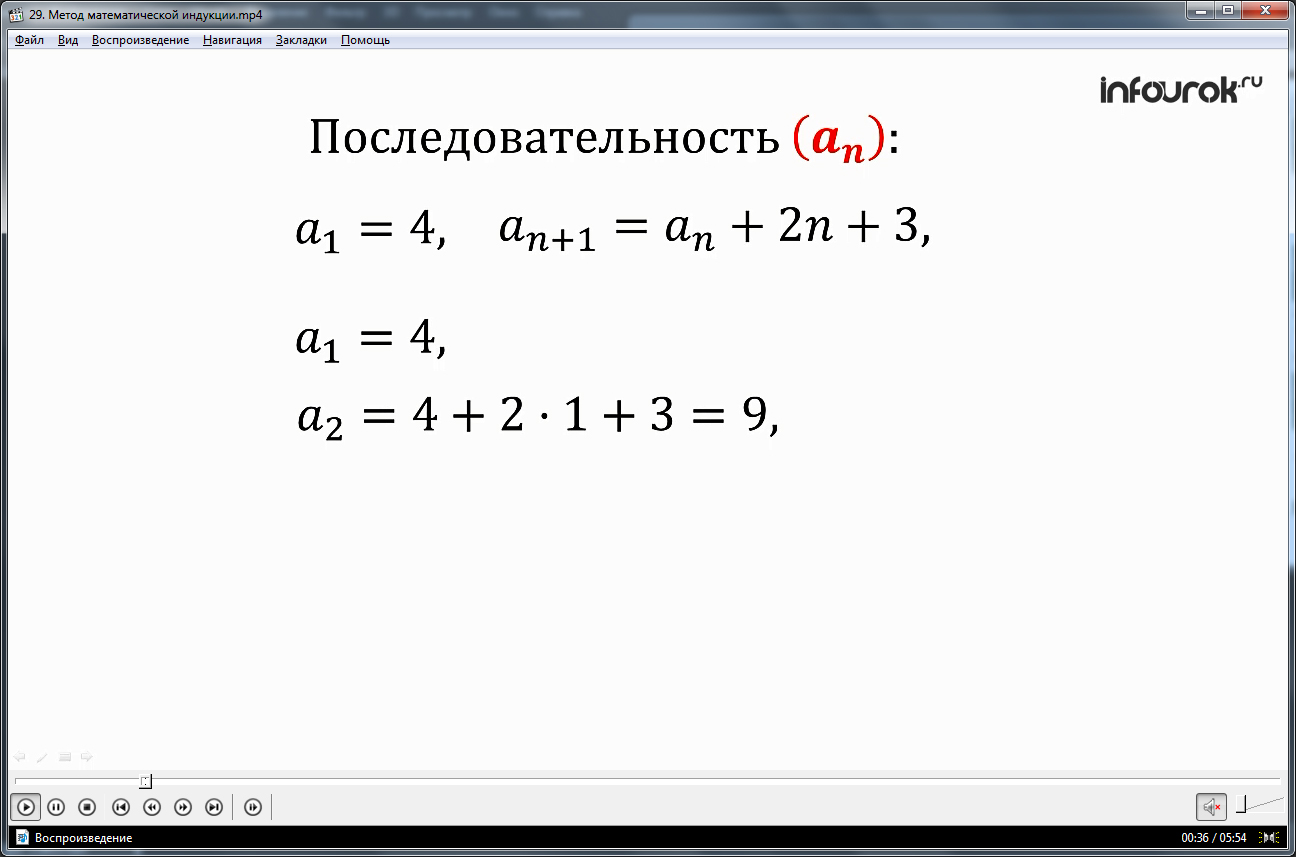
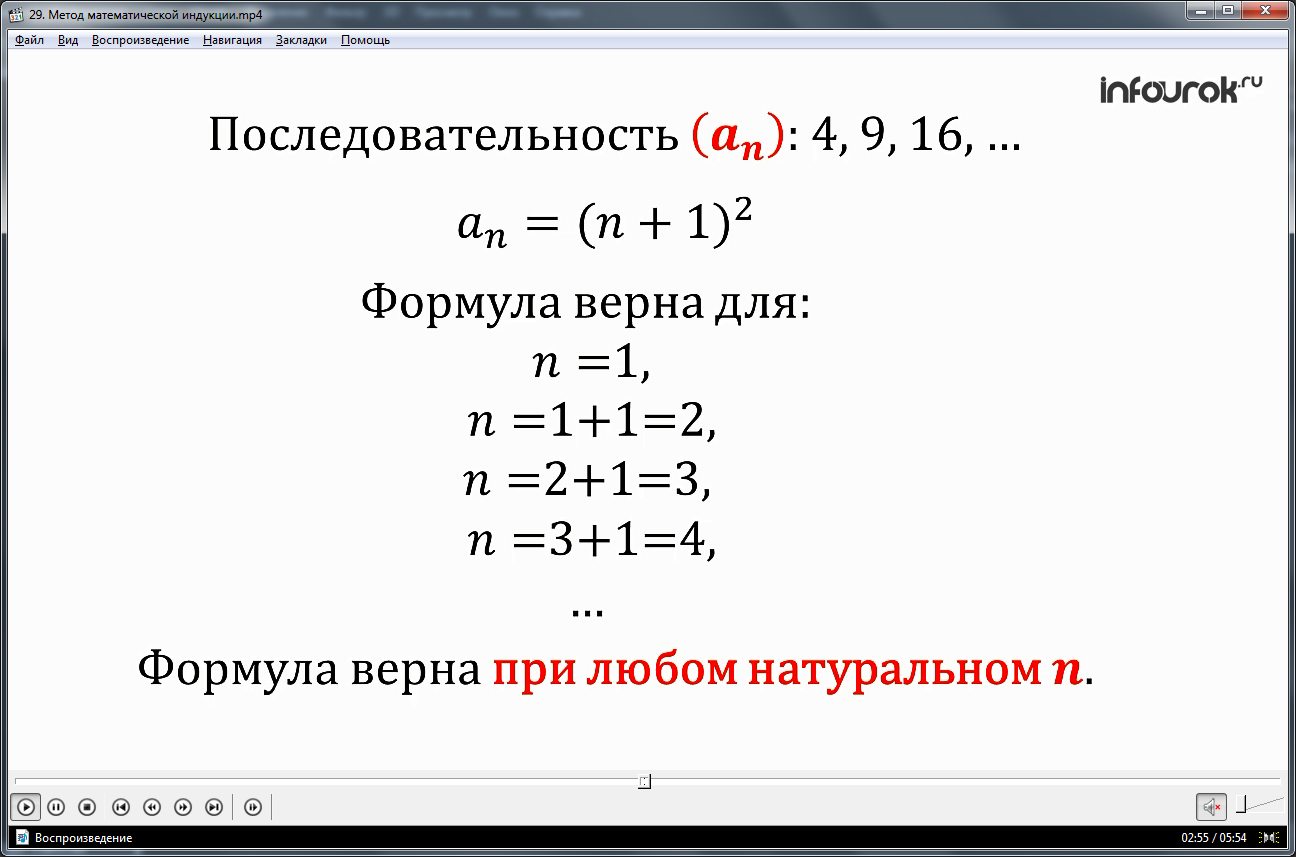
Понятие метода математической индукции вводится на примере рассмотрения последовательности an , в которой a1=4, а an+1= an+2n+3. В соответствии с общим представлением члена последовательности, определяется, что a1=4, a2=4+2·1+3=9, a3=9+2·2+3=16, то есть последовательность чисел 4, 9, 16,… Предполагается, что для данной последовательности верно an=(n+1)2. Для указанных членов последовательности – первого, второго, третьего – формула верна. Необходимо доказать справедливость данной формулы для любого сколь угодно большого n. Указывается, что в подобных случаях применяется метод математической индукции, помогающий доказать утверждение.
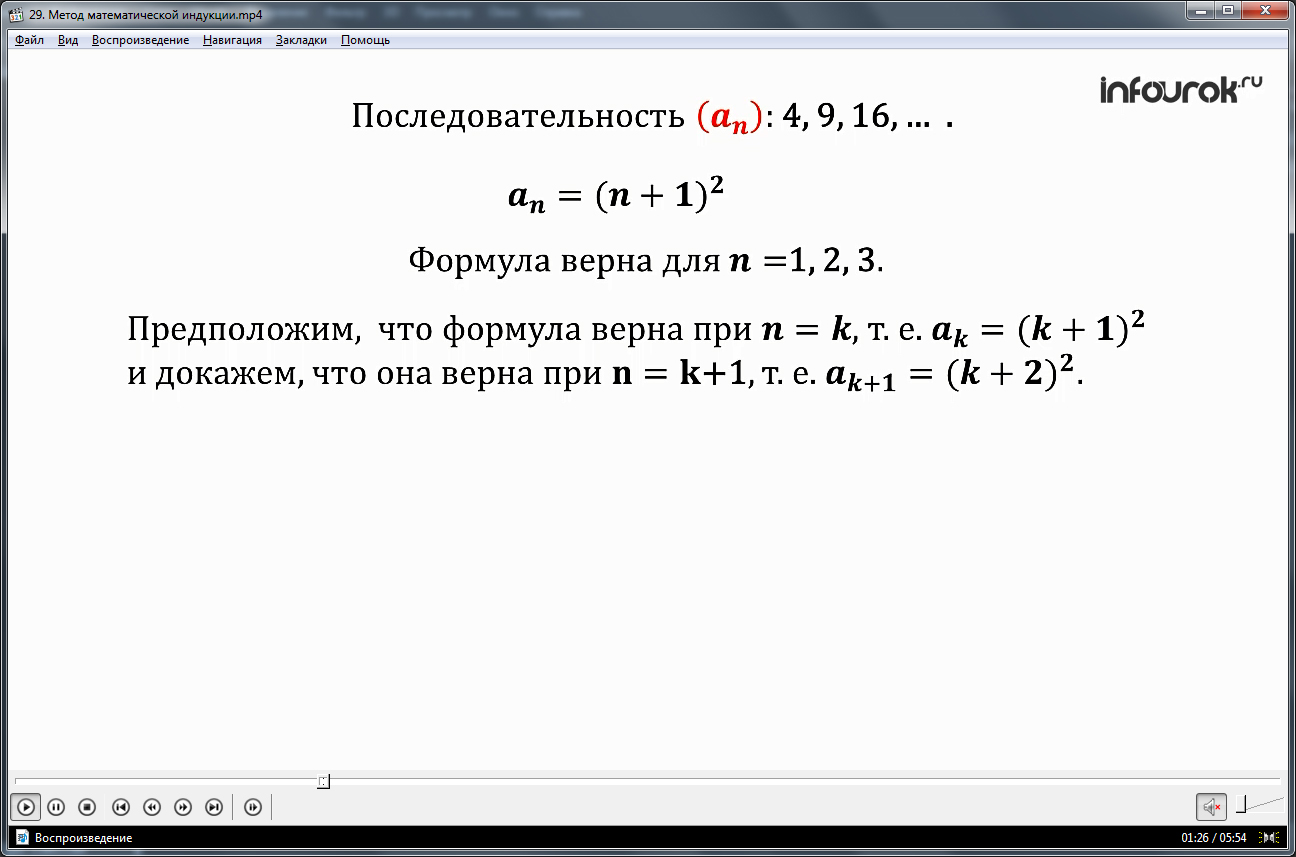
Раскрывается суть метода. Предполагается справедливость формулы для n=k, значение ak=( k+1)2. Необходимо доказать, что равенство будет справедливым также при k+1, что значит ak+1=( k+2)2. Для этого в формуле ak+1=ak+2k+3 заменяем ak на (k+1)2. После подстановки и приведения подобных получаем равенство ak+1=( k+2)2. Это дает право утверждать, что справедливость формулы для n делает ее верной и для n=k+1. Рассмотренное доказательство применительно к последовательности an, которая представлена числами 4, 9, 16,… и общим членом an=(n+1)2 дает право утверждать, если формула превращается в верное равенство для n=1, то также для n=1+1=2, и для 3 и т.д., то есть при всяком натуральном n.
Далее суть метода индукции излагается математическим языком. Принцип метода основан на справедливости утверждения, что факт имеет место для произвольного натурального n при выполнении двух условий: 1) утверждение является верным для n=1 2) из справедливости данной формулы для n=k следует справедливость ее для n=k+1. Из данного принципа следует и строение доказательства, с использованием метода математической индукции. Отмечается, что данный метод предполагает для n=1 доказательство справедливости утверждения, а при предположении справедливости доказательства для n=k доказывается, что верно также для n=k+1.
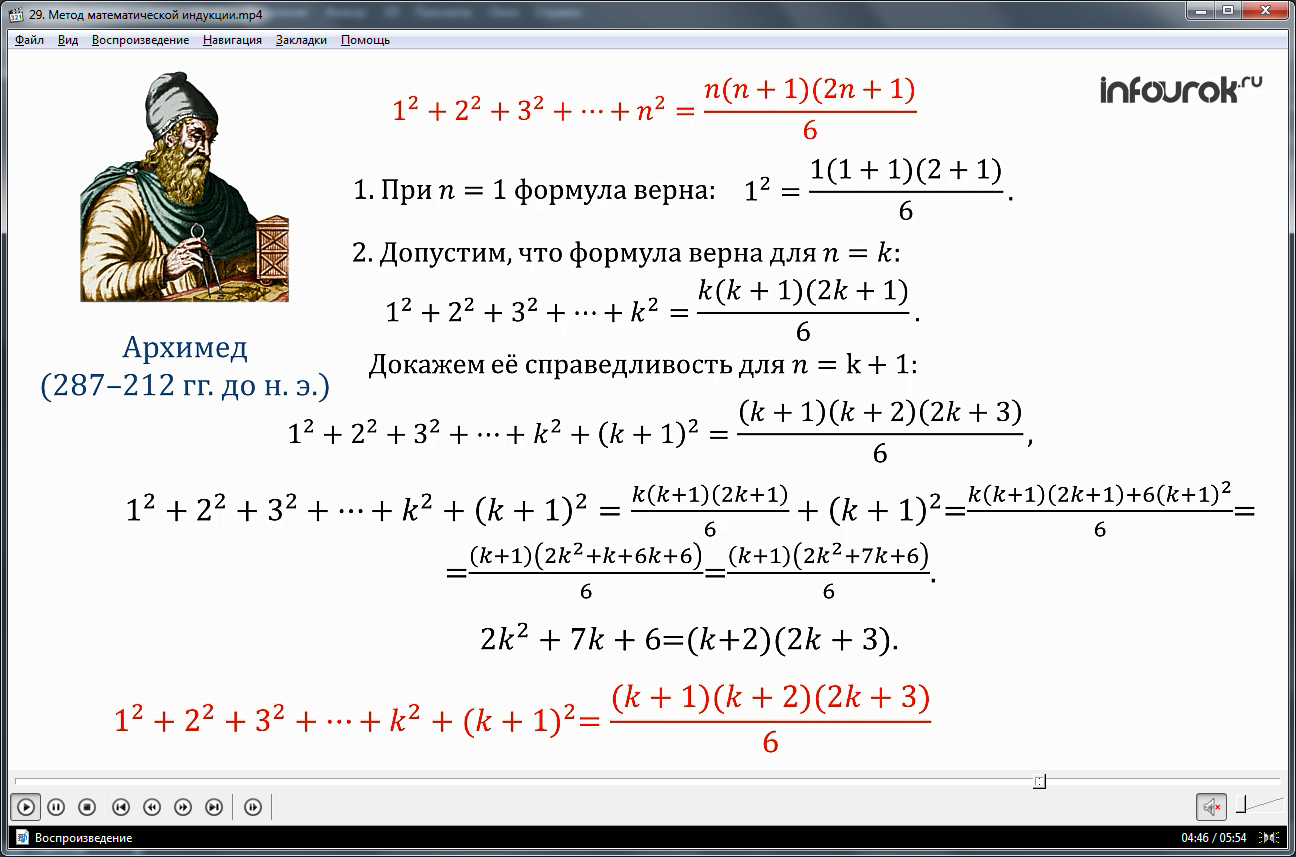
Разбирается пример доказательства формулы Архимеда методом математической индукции. Дана формула 12+22+32+…+n2=n(n+1)(2n+1)/6. На экране проводятся вычисления, выводящие справедливость формулы для n=1. Вторым пунктом доказательства является предположение, что для n=k формула справедлива, то есть она принимает вид 12+22+32+…+k2=k(k+1)(2k+1)/6.Основываясь на этом, доказывается, что формула верна и для n=k+1. После подстановки n=k+1 получаем значение формулы 12+22+32+…+k2+(k+1)2=(k+1)(k+2)(2k+3)/6. Таким образом, формула Архимеда доказана.
Еще в одном примере рассматривается доказательство кратности 7 суммы 15n+6 для всякого натурального n. В доказательстве пользуемся методом математической индукции. Сначала справедливость утверждения проверяем для n=1. Действительно, 151+6=21. Затем допускаем справедливость для n=k. Это означает, что 15k+6 является кратным 7. Подстановкой n=k+1 в формулу доказываем кратность 7 значения 15k+1+6. После преобразования выражения получаем: 15k+1+6=15k+1·14+(15k+6). Поэтому сумма15n+6 является кратной 7.
Видеоурок «Метод математической индукции» доходчиво и детально раскрывает суть и механизм применения метода математической индукции в доказательстве. Поэтому данный видеоматериал может послужить не только наглядным пособием на уроке алгебры, но будет полезен при самостоятельном изучении материала учеником, поможет объяснить тему учителю в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7635 |
| Номер материала | 673 |