
Урок "Умножение и деление степеней"

Краткое описание документа:
В прошлом видеоуроке мы узнали, что степенью некоего основания называется такое выражение, которое представляет собой произведение основания на самого себя, взятого в количестве, равном показателю степени. Изучим теперь некоторые важнейшие свойства и операции степеней.
Например, умножим две разные степени с одинаковым основанием:
(2)3 * (2)2
Представим это произведение в полном виде:
(2)3 * (2)2 = (2)*(2)*(2)*(2)*(2) = 32
Вычислив значение этого выражения, мы получим число 32. С другой стороны, как видно из этого же примера, 32 можно представить в виде произведения одного и того же основания (двойки), взятого в количестве 5 раз. И действительно, если пересчитать, то:
(2)5 = 32
Таким образом, можно с уверенностью прийти к выводу, что:
(2)3 * (2)2 = (2)5
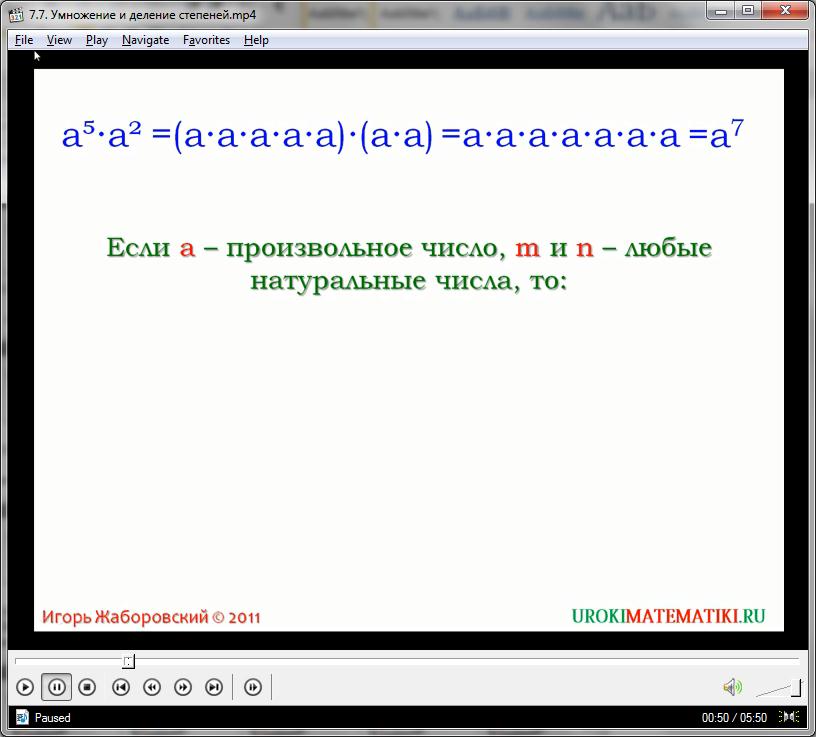
Подобное правило успешно работает для любых показателей и любых оснований. Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
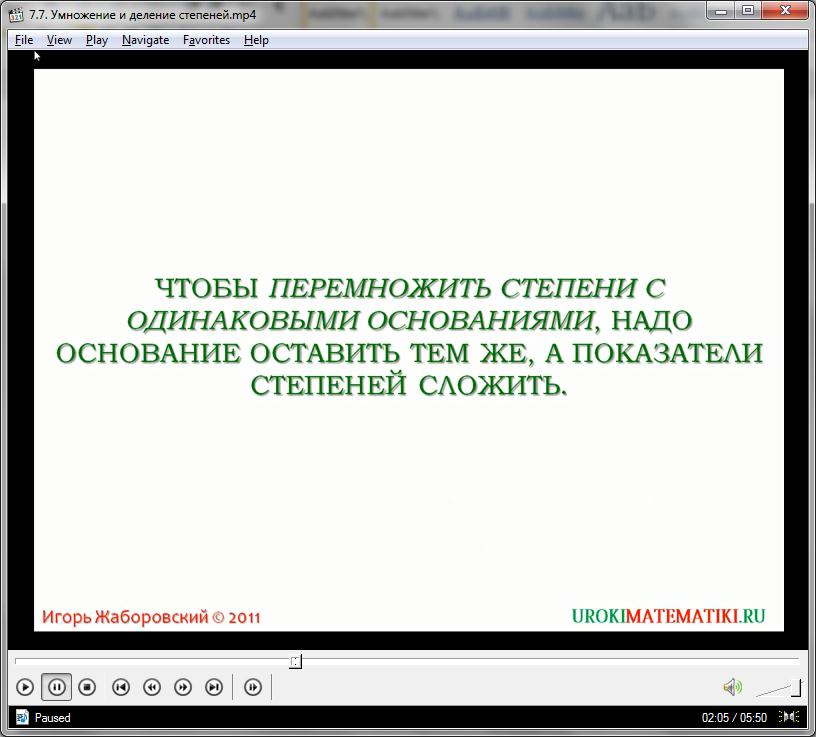
Представляемое правило прекрасно работает и при умножении нескольких выражений. Главное условие – что бы основания у всех были одинаковыми. Например:
(2)1 * (2)3 * (2)4 = (2)8
Нельзя складывать степени, да и вообще проводить какие-либо степенные совместные действия с двумя элементами выражения, если основания у них являются разными.
Как показывает наше видео, в силу схожести процессов умножения и деления правила сложения степеней при произведении прекрасно передаются и на процедуру деления. Рассмотрим такой пример:
(2)6 / (2)4
Произведем почленное преобразование выражения в полный вид и сократим одинаковые элементы в делимом и делителе:
(2)*(2)*(2)*(2)*(2)*(2) / (2)*(2)*(2)*(2) = (2)(2) = (2)2 = 4
Конечный результат этого примера не так интересен, ведь уже в ходе его решения ясно, что значение выражения равно квадрату двойки. И именно двойка получается при вычитании степени второго выражения из степени первого.
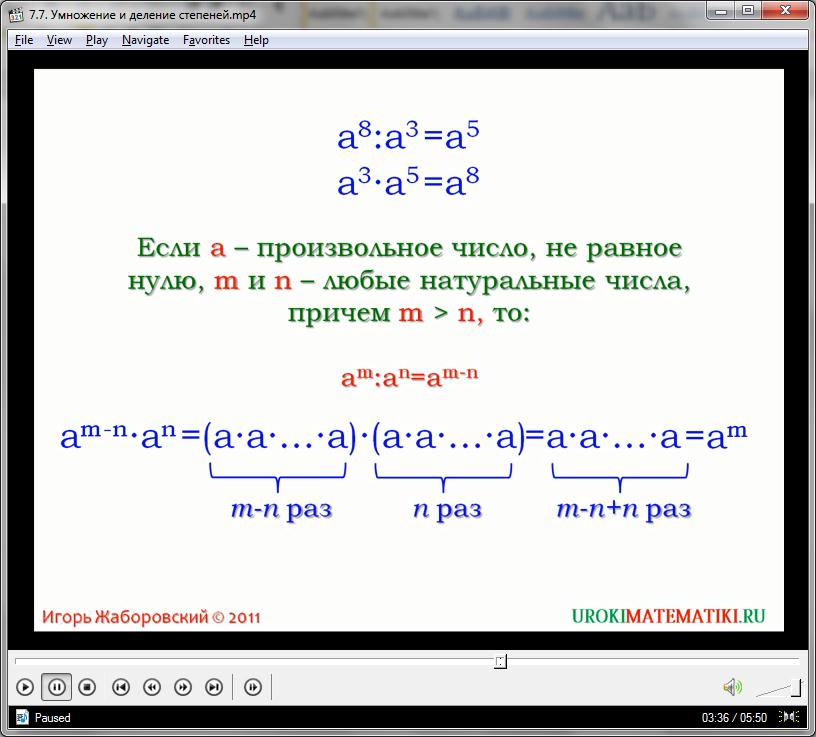
Чтобы определить степень частного необходимо из степени делимого вычесть степень делителя. Правило работает при одинаковом основании для всех его значений и для всех натуральных степеней. В виде абстракции имеем:
(а)х / (а)у = (а)х – у
Из правила деления одинаковых оснований со степенями вытекает определение для нулевой степени. Очевидно, что следующее выражение имеет вид:
(а)х / (а)х = (а)(х – х) = (а)0
С другой стороны, если мы произведем деление более наглядным способом, то получим:
(а)2 / (а)2 = (а) (а) / (а) (а) = 1
При сокращении всех видимых элементов дроби всегда получается выражение 1/1, то есть, единица. Поэтому принято считать, что любое основание, возведенное в нулевую степень, равно единице:
(а)0 = 1
Вне зависимости от значения а.
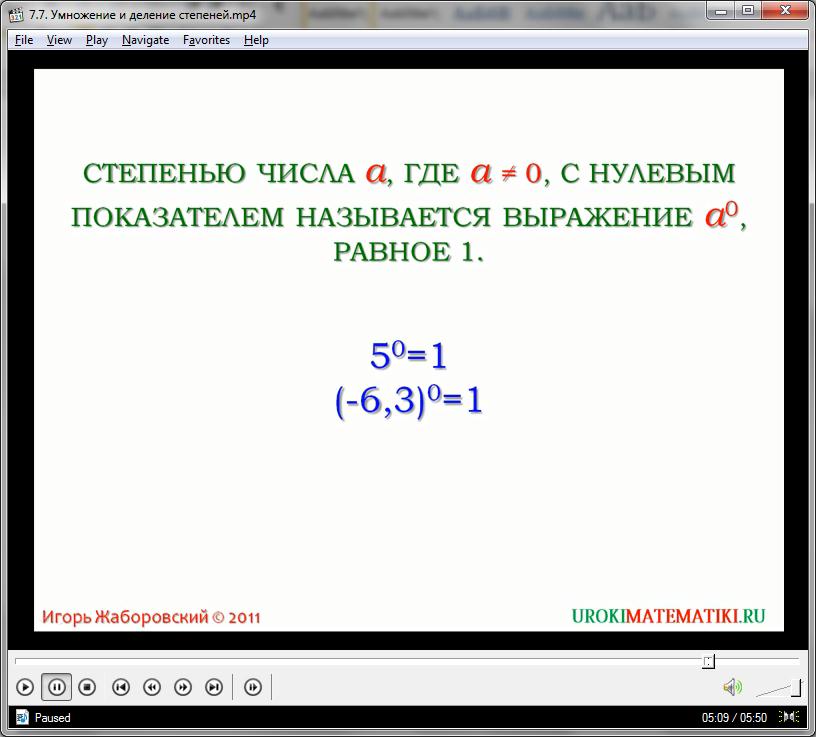
Однако будет абсурдно, если 0 (при любых перемножениях дающий все равно 0) будет каким-то образом равен единице, поэтому выражение вида (0)0 (ноль в нулевой степени) просто не имеет смысла, а к формуле (а)0 = 1 добавляют условие: «если а не равно 0».
Решим упражнение. Найдем значение выражения:
(34)7 * (34)4 / (34)11
Так как основание везде одинаково и равно 34, то итоговое значение будет иметь такое же основание со степенью (согласно вышеуказанных правил):
7 + 4 – 11 = 0
Иначе говоря:
(34)7 * (34)4 / (34)11 = (34)0 = 1
Ответ: выражение равно единице.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6655 |
| Номер материала | 445 |