
Урок "Наложения и движения"

Краткое описание документа:
Видеоурок«Наложения и движения» демонстрирует учебный материал по данной теме. В ходе видеоурока углубляются понятия наложения и движения, доказываются важные теоремы, связанные с этими понятиями и следствия из них. Задача видеоурока – сформировать глубокое понимание рассматриваемых понятий, формировать умение доказывать математические утверждения, облегчить усвоение материала, способствовать его запоминанию в ходе изучения. Видеоматериал может стать самостоятельной частью урока, а также может сопровождать объяснение учителя, послужив наглядным пособием.

Форма видеоурока – наиболее удобная для представления учебного материала, так как в ней может применяться комплекс средств, включающих ученика в активную учебную деятельность. При помощи анимации и кадрирования, учебный материал подается последовательно и логично. Использование озвучивания дает возможность давать важные комментарии и советы, а выделение цветом способствует более быстрому запоминанию понятий и формул, хода рассуждения при доказательстве.
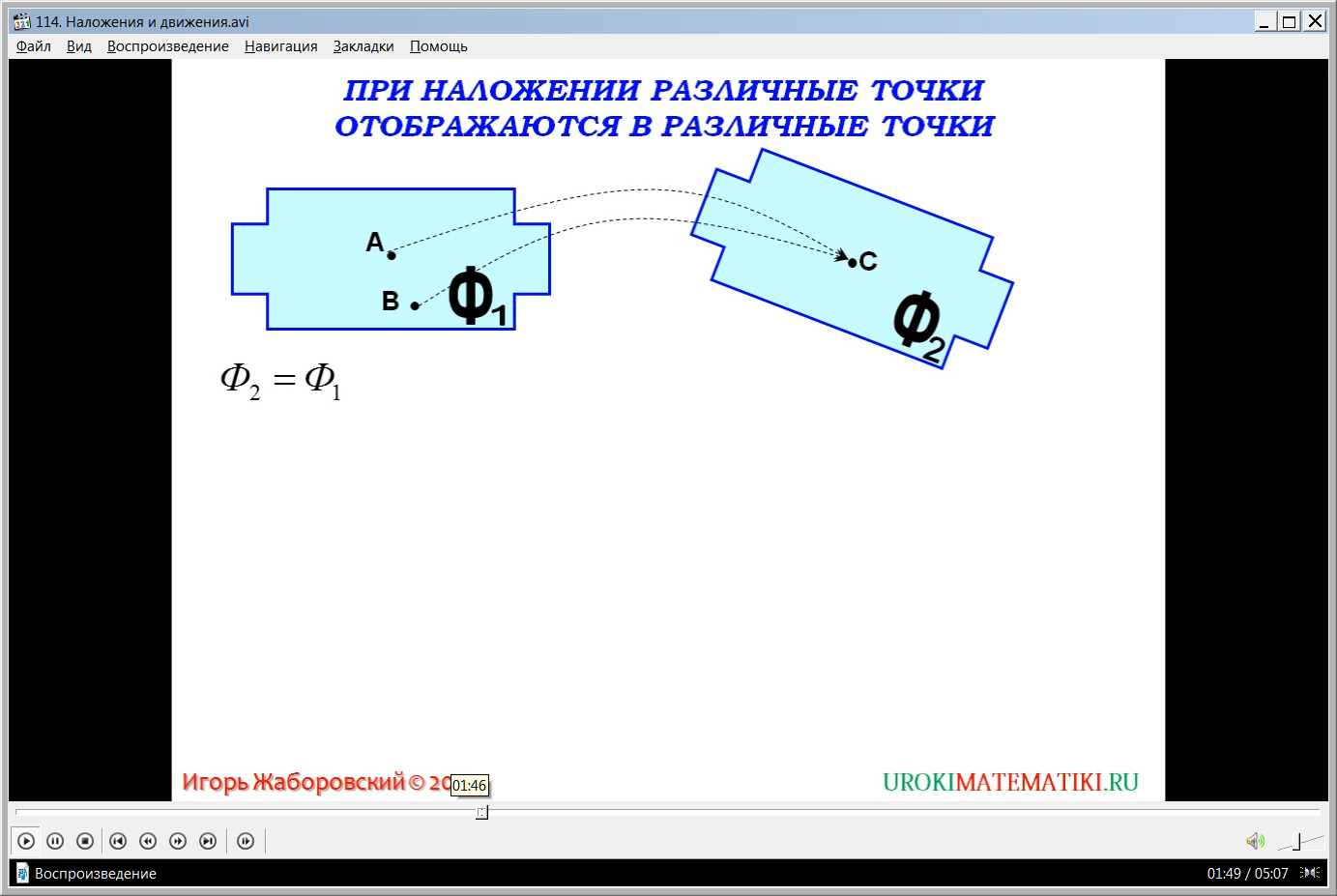
Видеоурок начинается с представления названия темы. Ученикам напоминается, что при рассмотрении понятия равенства фигур обсуждалась операция наложения двух фигур. Если при наложении две фигуры совпадали, они назывались равными. Для демонстрации данной операции на экране демонстрируются две фигуры Ф и Ф1, а также направление движения, которое указывает, как фигуры накладываются одна на другую. Отмечается, что наложением называется отображение фигуры Ф в фигуру Ф1, при котором происходит не только наложение точек данных фигур. Но при этом каждая точка плоскости, которой принадлежит фигура Ф, отображается в точку плоскости, содержащей фигуру Ф1.
Из рассмотренного примера делается вывод, что операция наложения являет собой отображение на себя плоскости. При этом замечено, что не всякое отображение плоскости - наложение. Понятие операции наложения содержит еще свойства, выраженные в определенных аксиомах. Именно эти аксиомы используют математики для наглядности при решении задач, в доказательстве теорем, следствий из них.
Далее описывается доказательство теоремы, утверждающей, что разные точки при наложении отображаются также в разные точки. Выполняется доказательство от противного. Предполагается, что две разные точки А, В отображаются в одну точку С. Это означает, что некоторая фигура Ф1, состоящая из этих двух точек, отображается в фигуру Ф2, состоящую из одной точки. Если при наложении Ф1=Ф2, то фигура Ф1 отображается в фигуру Ф2. Для отображения верно и обратное – то есть каждая точка фигуры Ф2 отображается в точку Ф1. Однако известно, что особенность отображения - в соответствие одной точке ставится только одна точка, значит, точке С соответствует всего одна точка плоскости. Мы пришли к противоречию, поэтому теорема доказана.
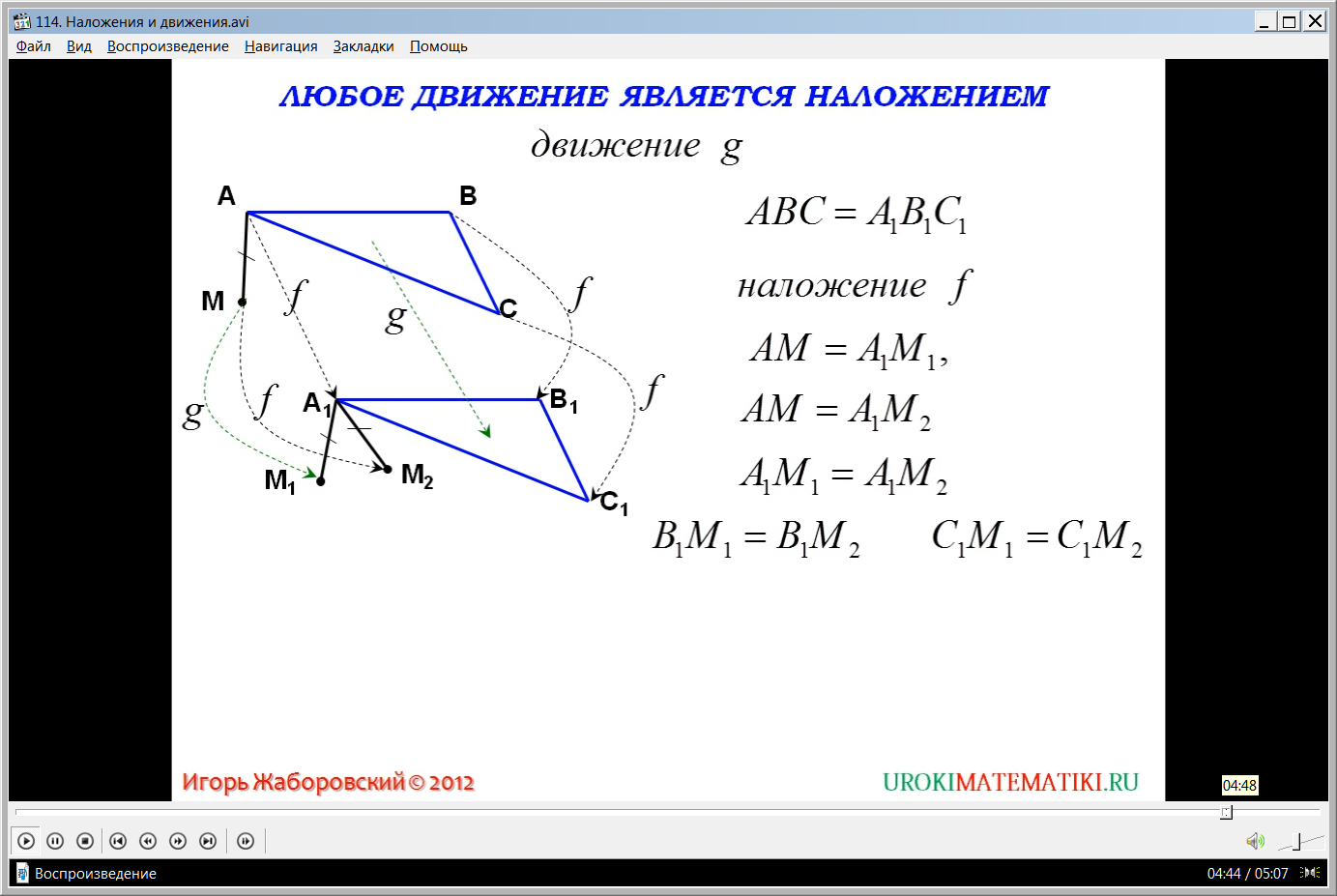
Следствием из доказанной теоремы является утверждение о равенстве отрезка, в который отображается некоторый отрезок при наложении. Для доказательства справедливости этого утверждения демонстрируется построение двух отрезков АВ и А1В1, а также направление движения при наложении. Отмечается, что при наложении А, В отображаются А1, В1. При этом весь отрезок АВ также отображается в отрезок А1В1.Поэтому АВ=А1В1. Отмечается, так как при наложении сохраняются расстояния между точками, наложение являет собой отображение на саму себя плоскости. Всякое наложение – движение плоскости. Этот вывод выведен на экран и выделен для запоминания. Необходимо доказать, что наложения g, f совпадают. Доказательство выполняется от противного – предполагается, что наложения не совпадают. Это означает, что существует некоторая точка М, которая под действием наложения g отображается в М1, при наложении f отображается в М2.Однако важным свойством движения является сохранение расстояний, поэтому расстояние от точки А до таких точек будет соответствовать равенствам АМ=А1М1, АМ=А1М2, следовательно, А1М1=А1М2, что означает равноудаленность точки А1 от точек М и М1. Отмечается, что аналогично можно доказать равноудаленность до данных точек М и М1 точки В1, а также точки С1. Но это бы означало, что А1, В1, С1 располагаются на серединном перпендикуляре к отрезку М1М2, однако эти точки не принадлежат одной прямой. Это означает, что мы пришли к противоречию, и все же движения gиf совпадают, а g есть наложение – что и требовалось доказать.
В конце видеоурока демонстрируется следствие из теоремы, утверждающее, что каждая фигура при движении отображается на равную фигуру.
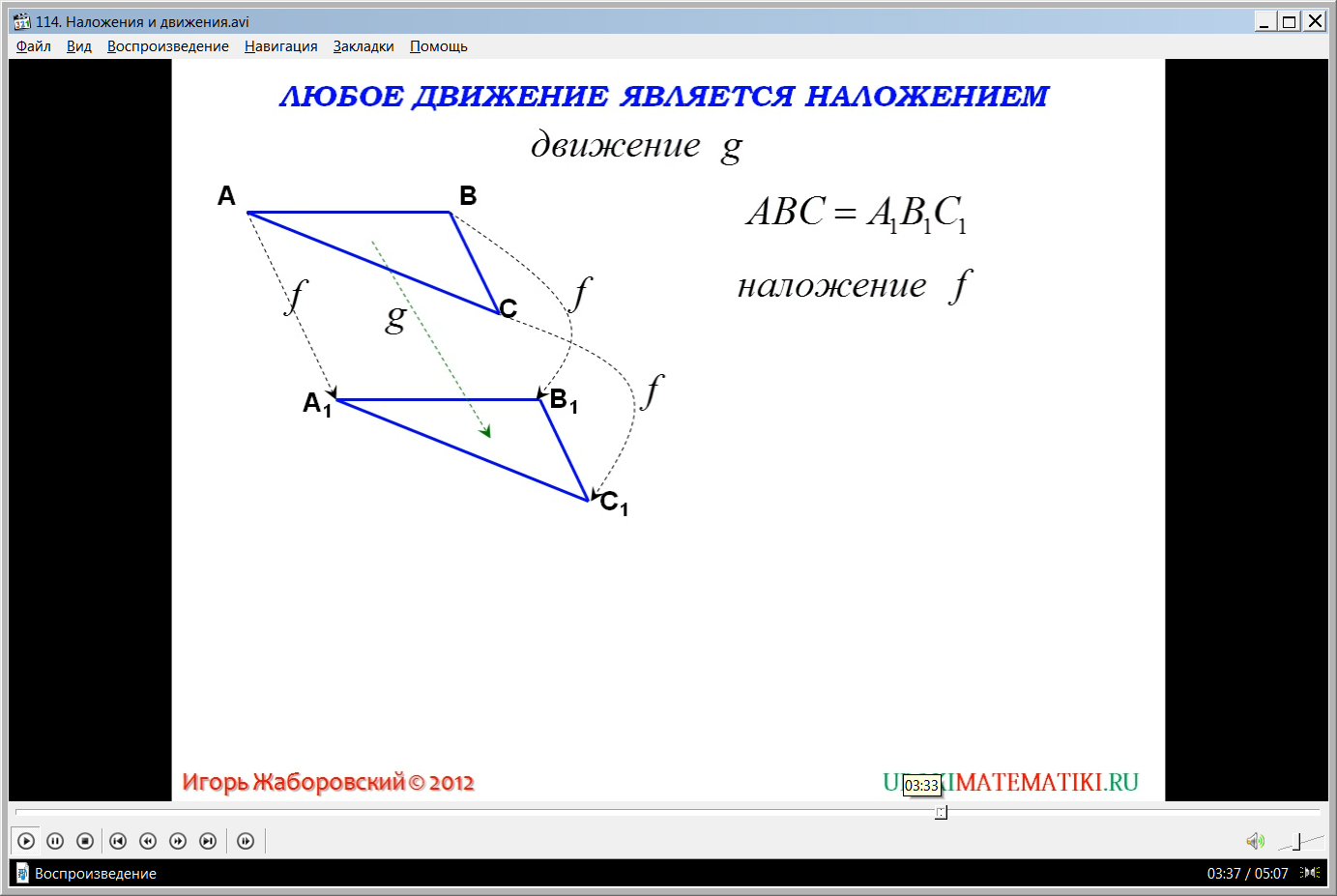
Также доказывается следствие из теоремы, обратное сделанному выводу. Доказывается, что любое наложение является движением. Для этого вводится обозначение некоторого наложения g, демонстрируются два равных треугольника АВС и А1В1С1. При наложении g один треугольник накладывается на другой, и они совпадают АВС=А1В1С1. Предполагается, что есть некоторое наложение f, при котором точки А, В и С совпадают с точками А1, В1, С1.
Видеоурок «Наложения и движения» может применяться для повышения эффективности традиционного школьного урока геометрии. Также данный материал с успехом может использоваться при дистанционном обучении. Ученикам, требующим дополнительных занятий или самостоятельно изучающим предмет, видеоурок также рекомендуется для самостоятельного рассмотрения темы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7197 |
| Номер материала | 752 |