
Урок «Натуральные логарифмы. Функция у=ln х, ее свойства, график, дифференцирование»

Краткое описание документа:
На предыдущем уроке мы открыли
новое иррациональное число. Это число
в ряду иррациональных чисел стоит
перед числом «пи»
Тогда справедливо полагать, что в это
число можно использовать в операциях
над иррациональными числами,
действительными числами. Например,
вычислить значение дроби
<!--?mso-application progid="Word.Document"?--> 14(tg 60В°-tg 45В°)(tg 45В°-e)26в€™cos 270В°">
Посчитать это значение будет довольно сложно, так как <!--?mso-application progid="Word.Document"?--> 14tg 60В°"> , число e, <!--?mso-application progid="Word.Document"?--> 1426"> числа иррациональные, но <!--?mso-application progid="Word.Document"?--> 14cos 270В°"> равен 0. Значит и значение выражения также будет равно 0.
Но чаще число е встречается не в
примерах и выражениях, а в с
основании логарифма.
Логарифм 2 по основанию 7, логарифм
5 по основанию 3, логарифм 5 по
основанию 10 называется десятичным
логарифмом, а вот логарифм 5 по
основанию е, называется натуральным
логарифмом пяти и записывается <!--?mso-application progid="Word.Document"?--> 14ln5"> .
В общем виде натуральный логарифм
записывается как <!--?mso-application progid="Word.Document"?--> 14lna">
Так как для любого логарифма можно
построить зависимость вида <!--?mso-application progid="Word.Document"?--> 14y=logax"> .
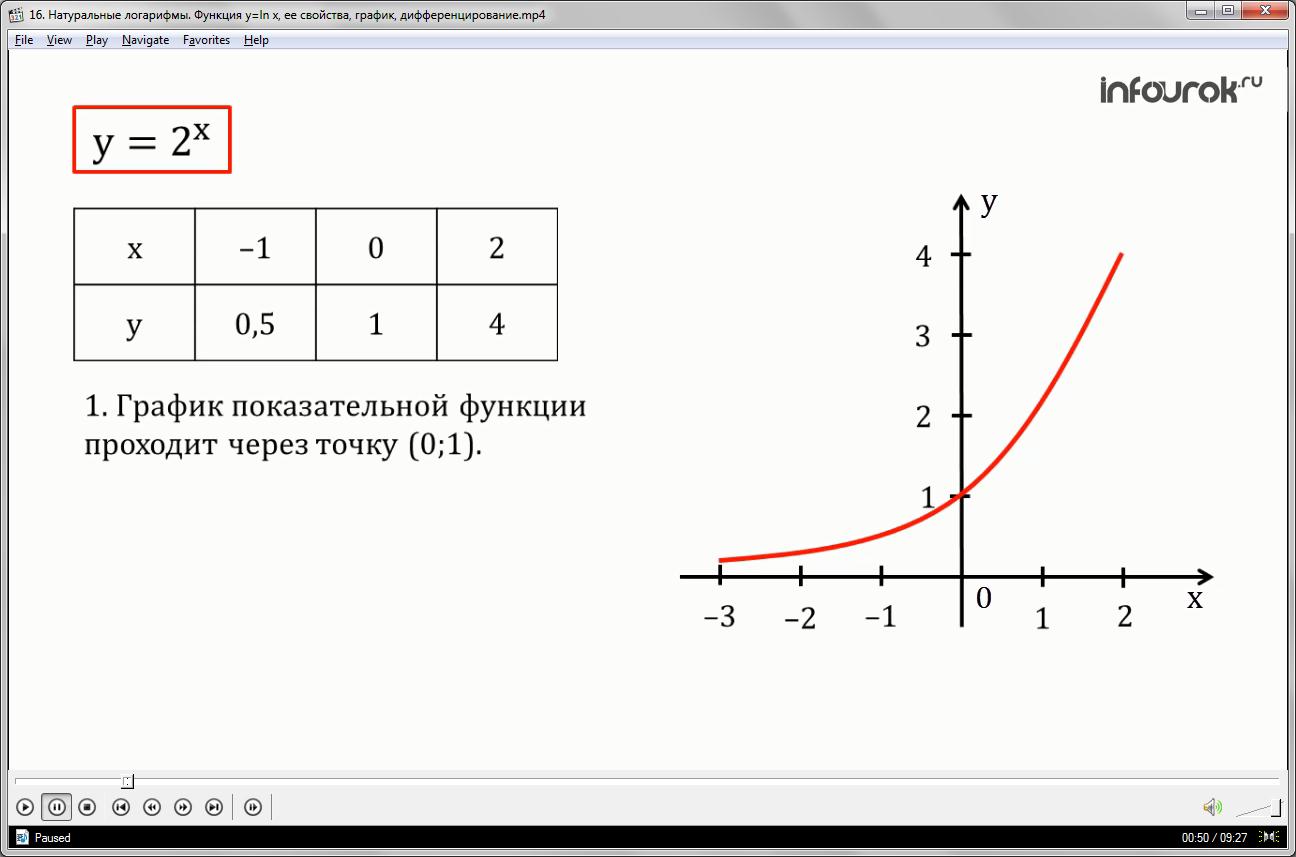
Причём график этой зависимости
симметричен графику показательной
функции <!--?mso-application progid="Word.Document"?--> 14y=ax"> относительно прямой
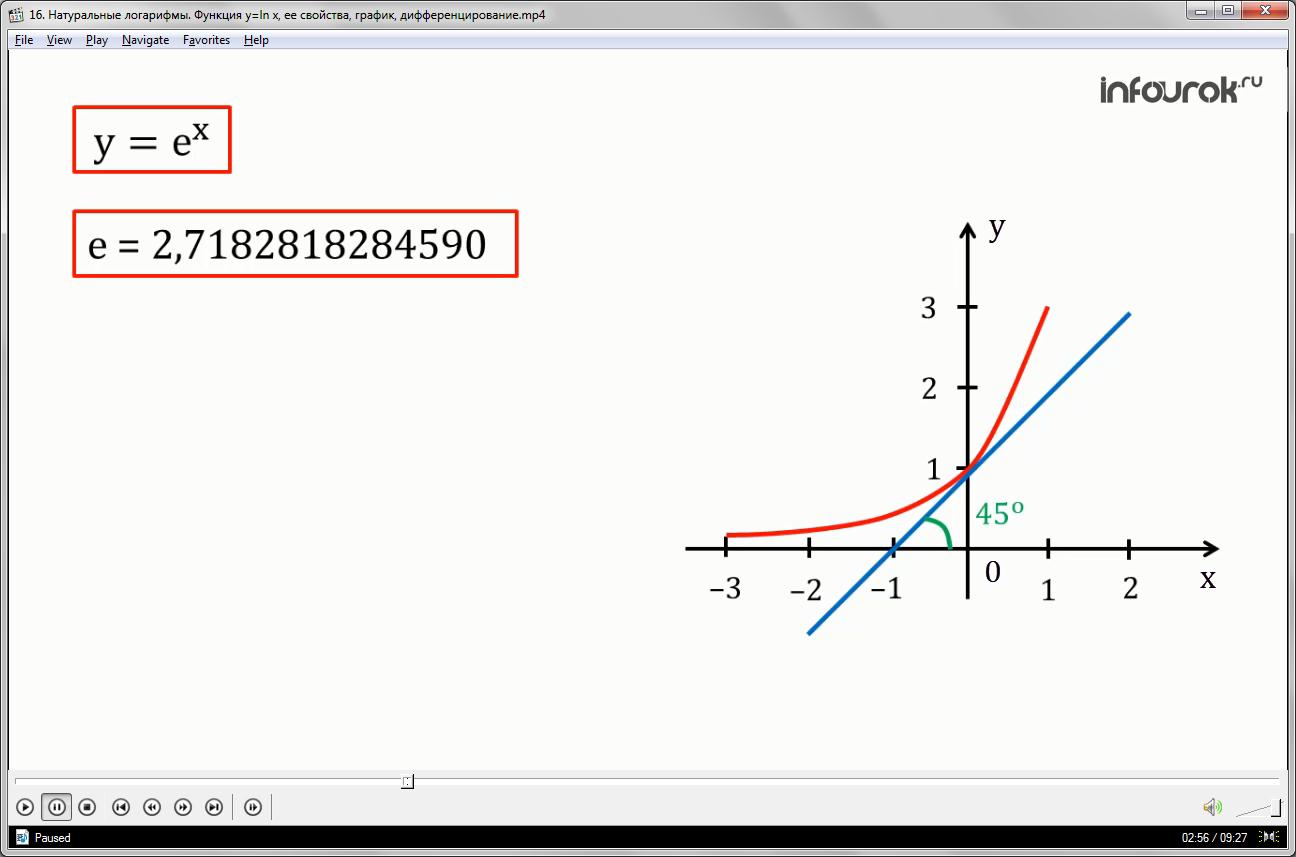
у=x. Тогда график логарифмической
функции <!--?mso-application progid="Word.Document"?--> 14y=lnx"> симметричен графику
<!--?mso-application progid="Word.Document"?--> 14y=ex"> относительно прямой y=x.
Свойства функции <!--?mso-application progid="Word.Document"?--> 14y=lnx"> не
отличаются от свойств функции
- D(f)=(0; +∞);
- Не является ни четной, ни нечетной;
- Возрастает на (0; +∞);
- Не ограничена ни сверху, ни снизу;
- Не имеет ни большего, ни наименьшего значений;
- Непрерывна;
- E(f)=(- ∞; +∞);
- Выпукла вверх;
- Дифференцируема.
Известно, что производная для <!--?mso-application progid="Word.Document"?--> 14lnx"> для
всех положительных значений х равна
1/х.
Рассмотрим примеры решения задач.
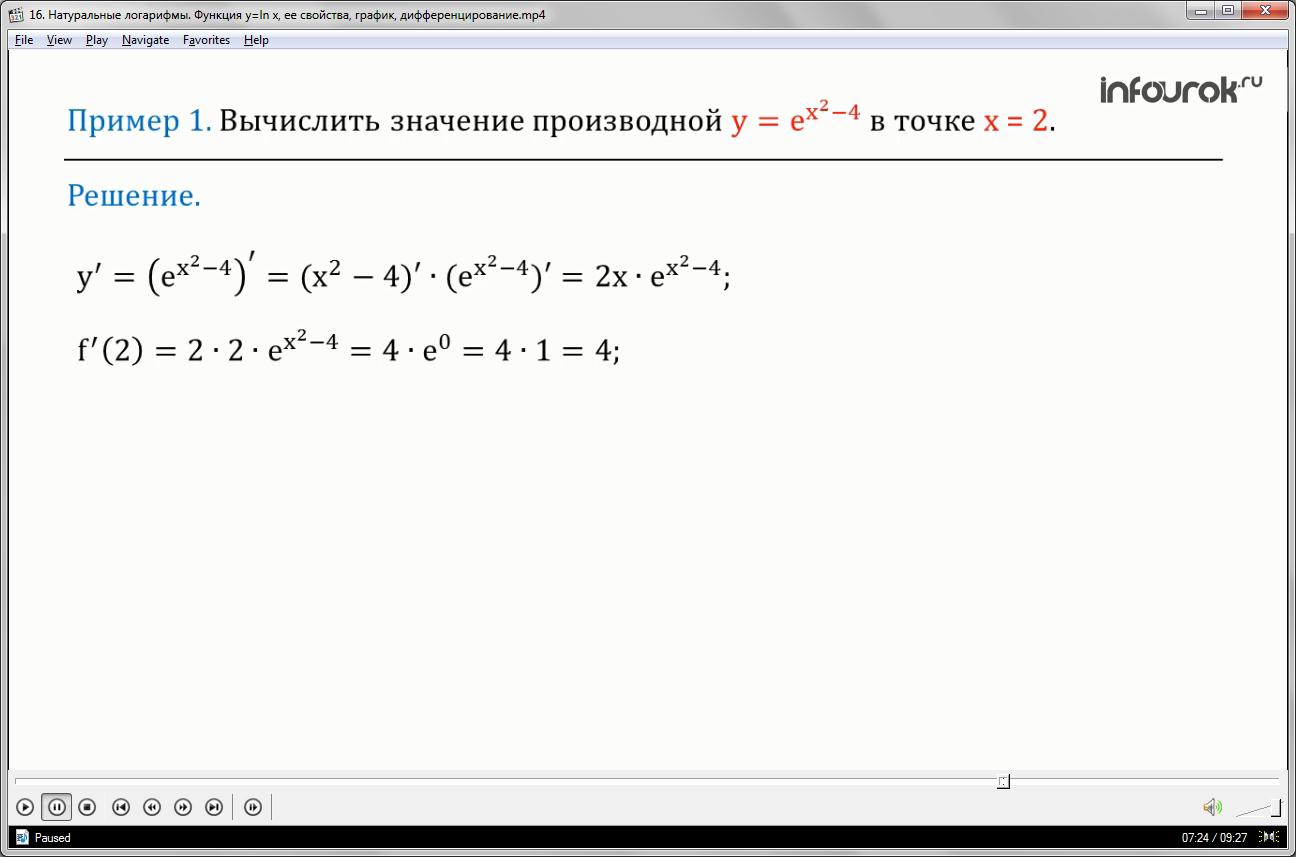
Пример 1. Вычислить значение
производной функции <!--?mso-application progid="Word.Document"?--> 14y=ln(8x+5) "> в точке х=-1
Воспользуемся правилом дифференцирования функций вида <!--?mso-application progid="Word.Document"?--> 14y=f(kx+m)"> , согласно которому <!--?mso-application progid="Word.Document"?--> 14y'=kв€™f'(kx+m)"> и тем, что <!--?mso-application progid="Word.Document"?--> 14(lnx)'=1x"> . Получим, что производная функции будет равна <!--?mso-application progid="Word.Document"?--> 1488x+5"> . Подставим в производную
вместо х минус один и получим, что
значение прозводной функции в точке
х=-1 равно <!--?mso-application progid="Word.Document"?--> 14-223">
Рассмотрим следующий пример.
Составьте уравнение касательной к графику функции <!--?mso-application progid="Word.Document"?--> 14y=f(x)"> в точке с абсциссой <!--?mso-application progid="Word.Document"?--> 14x=a"> :
<!--?mso-application progid="Word.Document"?--> 14fx=x5-lnx"> , a=1 ;
Для составления воспользуемся
алгоритмом составления уравнения
касательной к графику функции.
Число а равно одному. Значение
функции в точке равно 1. Производная
функции равна: производная разности
равна разности производных
уменьшаемого и вычитаемого ,
производная от икс в пятой степени
равна пять умножить на икс в четвертой
степени минус производная <!--?mso-application progid="Word.Document"?--> 14lnx"> , это 1/х. Следует учесть, что производная
существует при x ≠0 . Значение
производной функции от числа 1 равно
4. Составим уравнение касательной к
графику функции y=1+4(х-4)=1+4х-16=4x-15, получим y=4x-15
Пример 3. Исследовать функцию <!--?mso-application progid="Word.Document"?--> 14y=lnxx"> на экстремум функции. Для этого найдем производную функции. Она будет равна <!--?mso-application progid="Word.Document"?--> 141-lnxx"> .
При этом область определения функции
все действительные числа кроме 0.
Найдём нули производной, для этого
приравняем производную функции к нулю. Корень данного уравнения равен
числу е
Это единственная стационарная точка. Если x<e , то y’>0; если x>e , то y’<0. Значит, точка e- точка максимума функции <!--?mso-application progid="Word.Document"?--> 14ymax=lnee=1e"> .
Ответ: х=е – точка максимума <!--?mso-application progid="Word.Document"?--> 14ymax=1e"> .
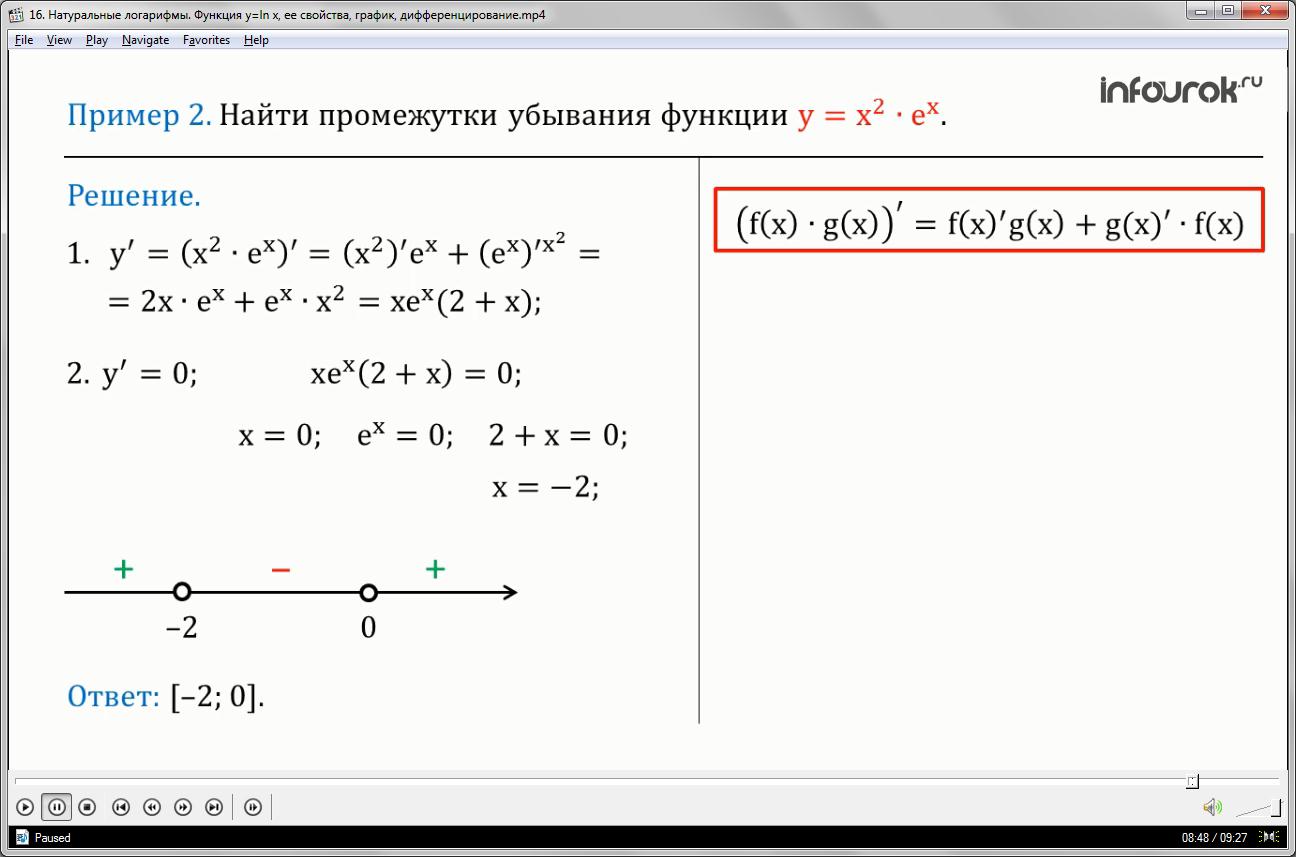
Пример 4. Найти производную функции
<!--?mso-application progid="Word.Document"?--> 14fx=2e-7x+9">
Производную найдём по правилу
дифференцирования сложной функции.
Для логарифмической функции
найдём производную. Для
этого перейдём от логарифма по
основанию а к логарифму по
основанию е. Запишем логарифм х по
основанию а виде частного
натуральных логарифмов от х и а.
выражение <!--?mso-application progid="Word.Document"?--> 14(lnxlna)'"> заменим на
произведение коэффициента 1/lna на
натуральный логарифм х. Производная
от lnx равна 1/х . таким образом
производная функции <!--?mso-application progid="Word.Document"?--> 14y=logax"> равна частного единицы к произведению .
Пример 5
Найдите значение производной заданной функции в указанной точке : <!--?mso-application progid="Word.Document"?--> 14y=lnвЃЎ(2x+2)"> , <!--?mso-application progid="Word.Document"?--> 14x0=14"> ;
Найдем производную функции по правилу <!--?mso-application progid="Word.Document"?--> 14y'=kв€™f'(kx+m)"> и <!--?mso-application progid="Word.Document"?--> 14(logax)'=1x ln a"> .
Производная логарифма равна
Частному <!--?mso-application progid="Word.Document"?--> 141x ln a"> , тогда производная равна частному <!--?mso-application progid="Word.Document"?--> 142(2x+2)lne"> . Причём натуральный логарифм числа е
это есть 1. Полученную дробь можно
сократить на два, получим что
производная <!--?mso-application progid="Word.Document"?--> 14lnвЃЎ(2x+2)"> будет равна
1/(х+1). Подставим значения
переменной в формулу -0,25+1 в
знаменателе дадут 0,75. А дробь <!--?mso-application progid="Word.Document"?--> 1410,75"> равна 4/3
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6287 |
| Номер материала | 1065 |