
Урок «Некоторые приемы решения целых уравнений»

Краткое описание документа:
Видеоурок «Некоторые приемы решения целых уравнений» помогает освоить приемы, помогающие решить более эффективно целые уравнения с различными особенностями. При помощи данного материала расширяется и углубляется понятие учеников о способах решения уравнений, формируются навыки поиска эффективных способов решения.
Задача видеоурока – при помощи подробного объяснения с использованием анимации и других приемов, применяемых для лучшей наглядности, облегчить понимание материала, представить его в наиболее удобном виде для понимания и запоминания.
Видеоурок начинается в представления темы. Ученикам напоминается, что нахождение корней многочлена высокой степени осложняется, так как удобных формул на нахождения корней нет или они вовсе не выведены. Поэтому для решения уравнений, содержащих многочлены высоких степеней, применяются методы, основанные на особенностях решаемых уравнений. В зависимости от особенностей уравнения, могут быть применены разные способы решения – к примеру, уже рассмотренный метод интервалов.
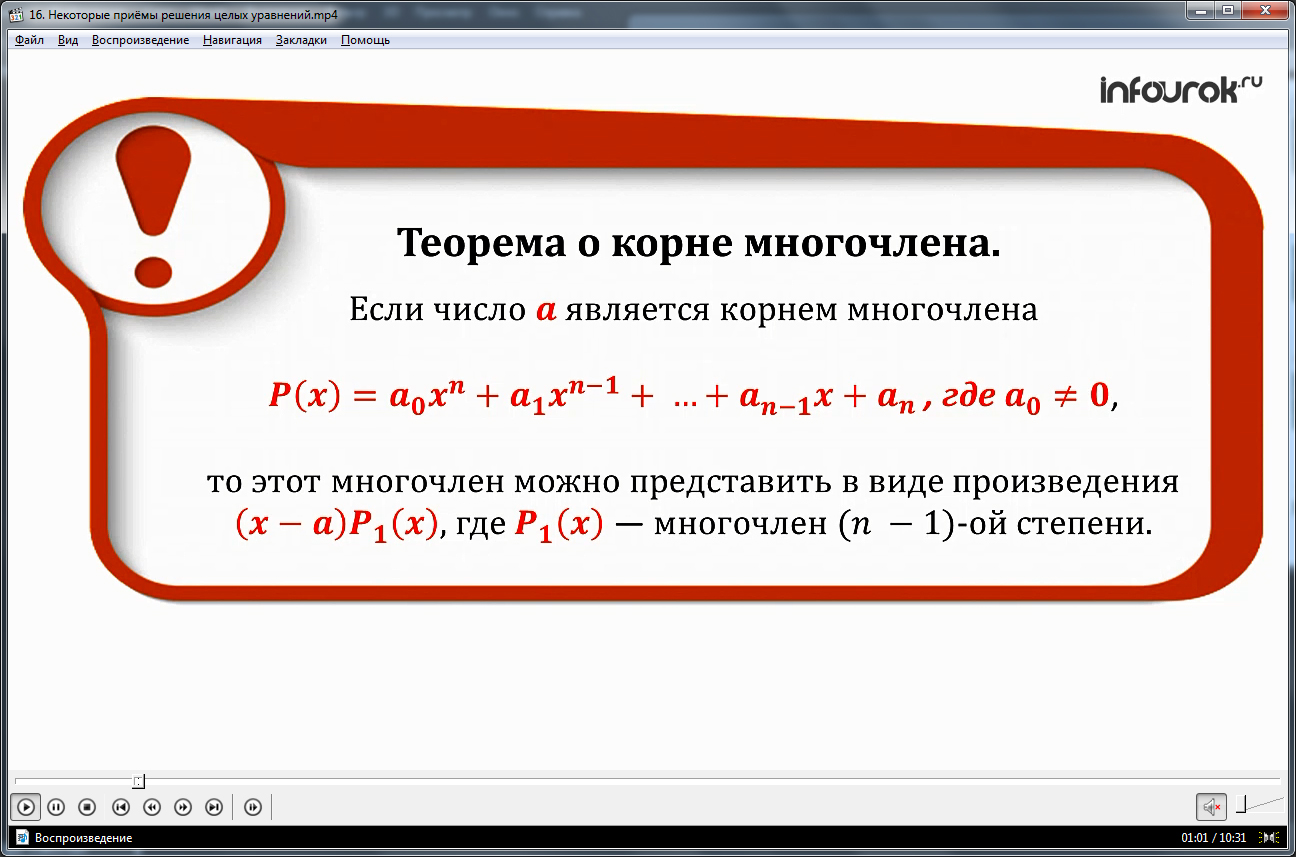
Некоторые уравнения высоких степеней решают, используя выводы теоремы о корне многочлена, которая формулируется на экране. Суть теоремы состоит в том, что при известном корне а многочлена вида P(x)=a0xn+a1xn-1+…+an-1x+an, в котором a0≠0, многочлен может быть представлен в виде произведения (х-а)Р1(х). При этом Р1(х) – многочлен степени (n-1). Отмечается, что для уравнения с одной переменной, целыми коэффициентами и одним корнем, поиск корня можно выполнить, используя теорему о целых корнях целого уравнения.
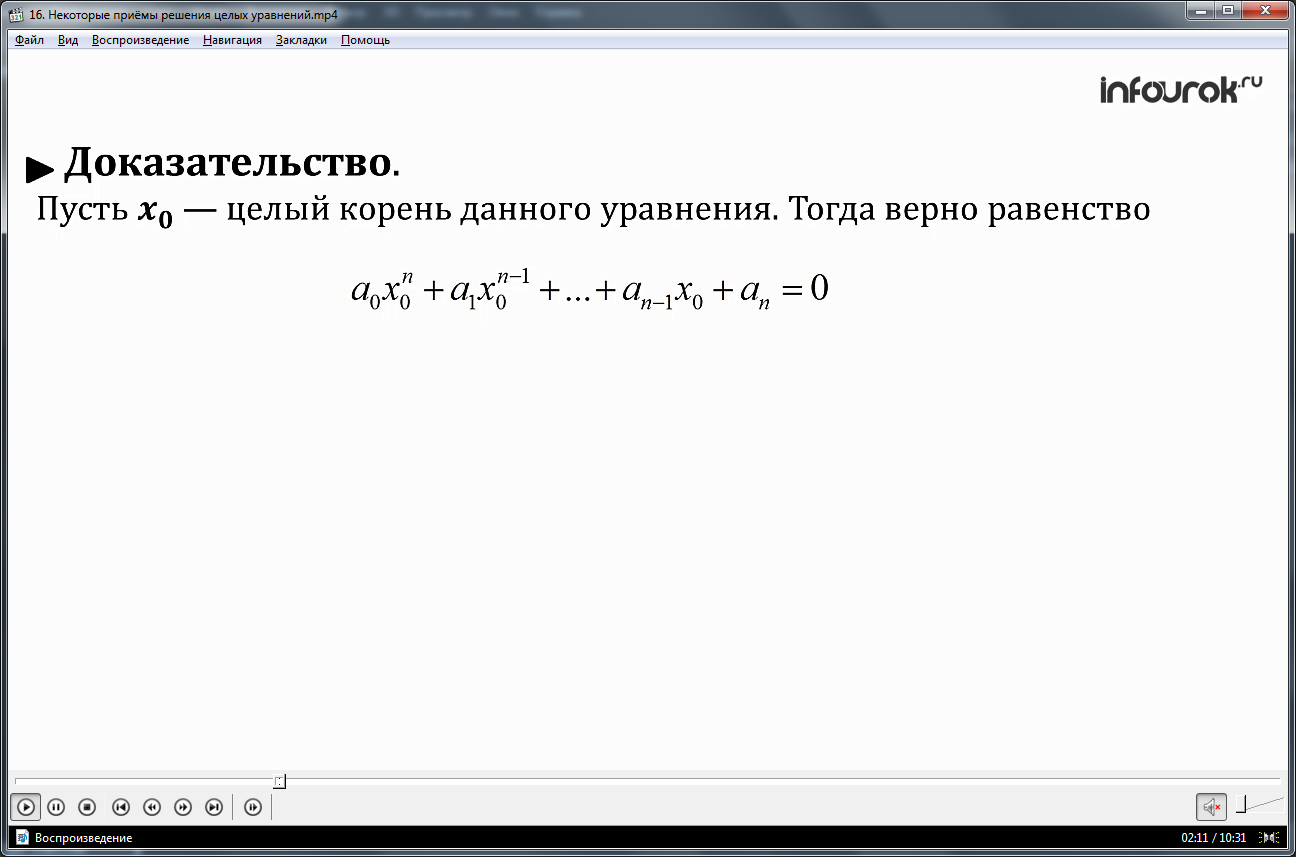
Текст теоремы о целых корнях целого уравнения выведен на экран и выделен для записи в тетради и лучшего запоминания. Он гласит о том, что если уравнение a0xn+a1xn-1+…+an-1x+an=0, в котором an≠0, а a0, a1, a2… являются целыми числами, имеет целый корень, этот корень - делитель свободного члена. Приводится доказательство данной теоремы. Чтобы доказать справедливость суждения, допускается, что х0 – целый корень уравнения. При его подстановке в уравнение, получается a0x0n+a1x0n-1+…+an-1x0+an=0. При переносе свободного члена в правую часть уравнения, в оставшемся выражении можно вывести за скобки общий множитель х0. Получится уравнение вида an= x0(-a0x0n-1-a1x0n-2-…-an-1). Выражение в скобках является целым числом, так как x0, -a0, -a1, -a2… - целые числа. Следовательно, при делении an на x0 в результате получается целое число, и x0 является делителем свободного члена.
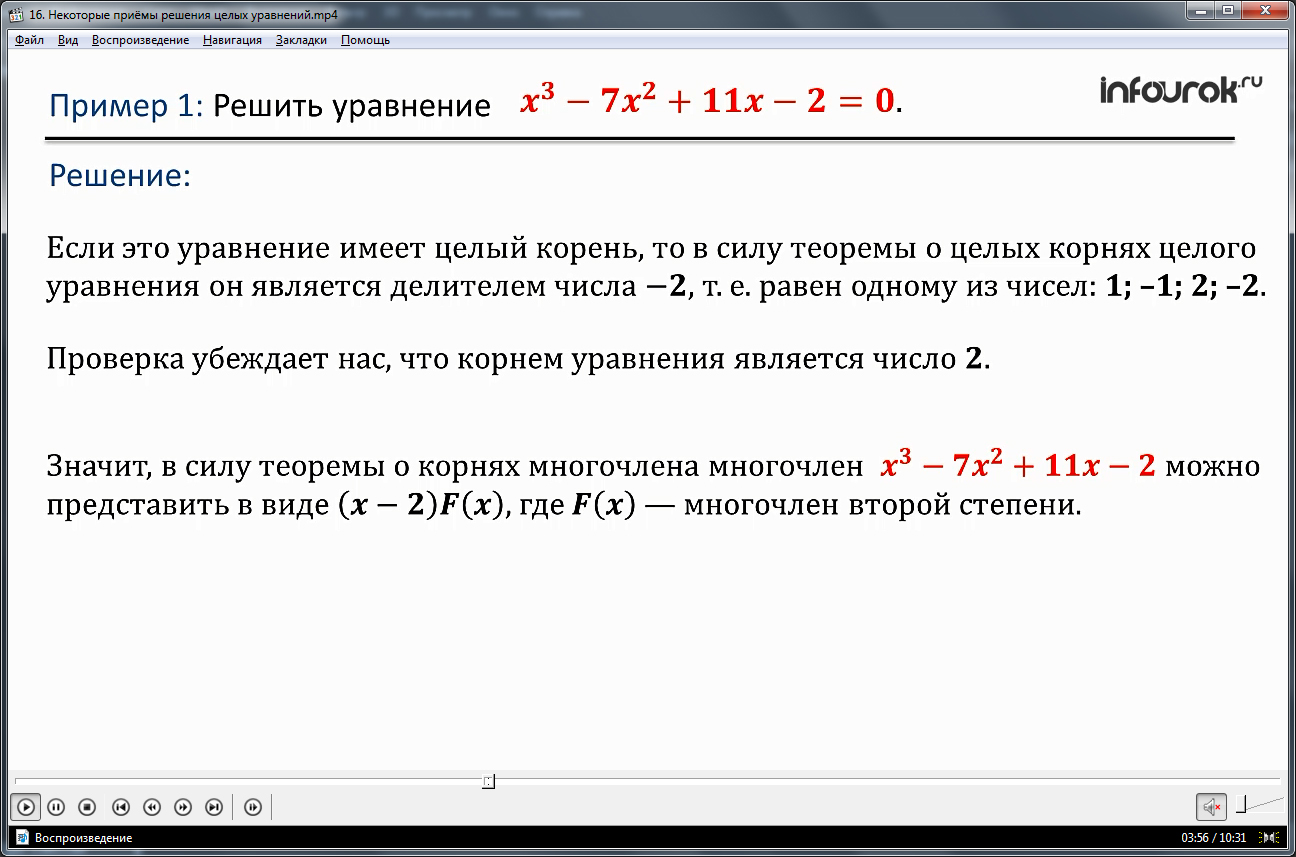
Ученикам представляется материал, помогающий научиться применять данную теорему для решения уравнений методом разложения многочлена на множители. Для этого необходимо усвоить, что уравнение Р(х)=0 решается разложением многочлена Р(х) на множители, если Р(х) – многочлен третьей и более высоких степеней. Примером подобного решения служит описанное в примере 1 решение уравнения х3-7х2+11х-2=0. Вспоминая изученную теорему о целых корнях целого уравнения, обратим внимание на свободный член уравнения. Его делителями являются числа 2, -2, 1, -1. Подставив значения корней в уравнение, можно убедиться, что корнем будет число 2. Поэтому многочлен в левой части уравнения, согласно теореме о корнях многочлена, представляем в виде (х-2)F(x), при этом F(x) является многочленом второй степени. Найти F(x) можно, выполняя деление уголком. Данный способ деления демонстрируется на экране, наглядно описывая все его особенности. В результате деления получается F(x)=х2-5х+1. Соответственно уравнение приобретает вид (х-2)( х2-5х+1)=0. Уравнение будет справедливо, если хотя бы один множитель равен нулю. То есть решение сводится к нахождению корней уравнений х-2=0 и х2-5х+1=0. Корень первого уравнения х1=2 Корнями второго уравнения являются числа х2=1/2(5+√21) и х3=1/2(5-√21). Все три найденных значения являются корнями исходного уравнения.
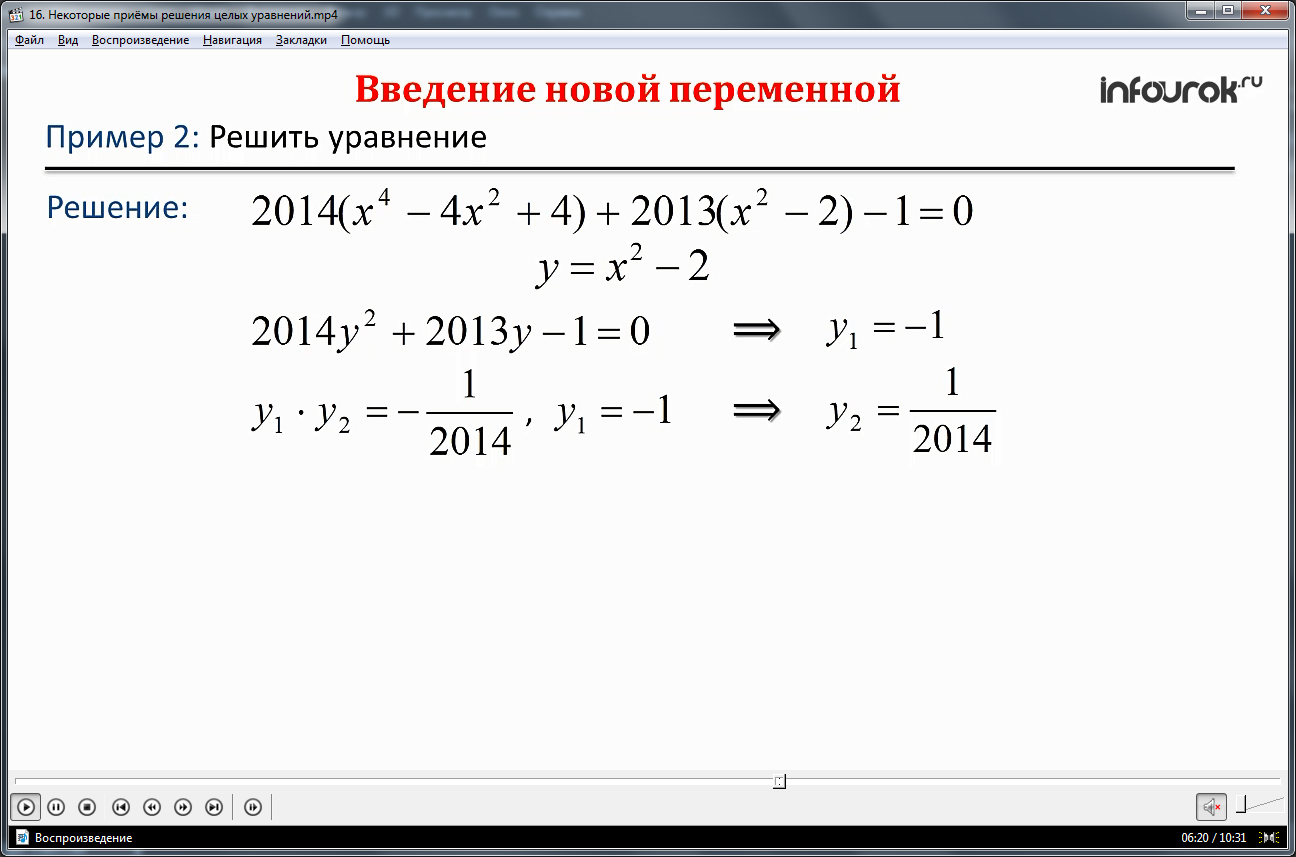
Напоминается способ введения новой переменной, который уже применялся учениками при решении биквадратных уравнений. Его использование демонстрируется в решении уравнения 2014(х4-4х2+4)+2013(х2-2)-1=0. Очевидно, что в выражении есть часть, которая может быть заменена переменной у, понижающей степень многочлена. После замены выражения х2-2 переменной у, получается квадратное уравнение 2014у2+2013у-1=0. Используя теорему Виета находятся корни данного уравнения – у1=-1 и у2=1/2014. После подстановки значений у в выражение, принятое на новую переменную, находим значения корней х. Полученные решения уравнений равны х1=1, х2=-1, х3=√4029/2014 и х4=-√4029/2014.
Отмечается, что методом введения новой переменной могут быть решены возвратные уравнения. Определение возвратных уравнений дается на экране, выделенное для запоминания. Это уравнения вида a0xn+a1xn-1+…+an-1x+an=0, в которых ak= an-k, k=0, 1, 2, …, n. Примером решения возвратного уравнения служит решение уравнения х4-7х3+8х2-7х+1=0. Отмечается, что в решении уравнения может помочь схожесть коэффициентов, которая приведет к выражению, позволяющему применить метод введения новой переменной. После деления обеих частей уравнения на х2, перегруппировки слагаемых и вынесения общих множителей за скобки, получаем выражение (х2+1/х2)-7(х+1/х)+8=0. За новую переменную принимается х+1/х=у. После ее подстановки получается квадратное уравнение у2-7у+6=0. Корнями данного уравнения являются у1=1 и у2=6. После подстановки значений переменной у в выражение, содержащее х, получим два уравнения для нахождения корней исходного уравнения. В результате вычисления определяются корни уравнений – х1=3+2√2 и х2=3-2√2.
На примере рассматривается решение уравнения, в котором используются участки возрастания и убывания функции. В уравнении х5+2х-3=0 согласно теореме о целом корне целого уравнения, проверяется наличие целого корня. Для этого оцениваются делители свободного члена. Проверкой выявлено, что делитель 1 является корнем данного уравнения. Для демонстрации единственности данного корня решения уравнения оценивается при помощи переброски его линейной части в правую сторону: х5=-2х+3. Слева в уравнении располагается возрастающая функция у= х5, график которой построен на рисунке. Функция, расположенная в правой части у=-2х+3 представляет собой убывающую прямую. Решение уравнения будет точкой пересечения этих двух графиков. Таким образом, можно констатировать, что решение уравнения будет одно: х=1.
Видеоурок «Некоторые приемы решения целых уравнений» помогает учителю представить информацию об особенностях решения различных уравнений, более эффективно использовать время урока. Также данный материал поможет ученику самостоятельно разобраться с решением уравнений. Также данное видео может быть полезно при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6996 |
| Номер материала | 678 |